NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2 (Applications of Derivatives)
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2 contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in exercise 6.2.
Krati Saraswat31 Jan, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2 (Applications of Derivatives)
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2 Applications of Derivatives is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 6. Given below is step by step solutions of all questions given in the NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2.NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2 Overview
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2 addresses these significant subjects. In order to fully comprehend the concepts presented in the chapter and make effective use of the provided solutions, it is recommended that students go over each topic in great detail. The intention is for students to effortlessly achieve excellent exam scores after reviewing and practicing these responses.NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2:NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
Question 1. Show that the function given by f(x) = e 2x is strictly increasing on R. Solution : Given: f'(x) = e 2x Now, x ∈ R Since the value of e 2x is always positive for any real value of x, e 2x > 0. ⇒2e 2x > 0 ⇒f'(x) > 0 So f(x) is incerasing on R.NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1
Question 2. Show that the function given by f ( x ) = 3 x + 17 is strictly increasing on R. Solution :
Question
3.
Show that the function given by
f
(
x
) = sin
x
is
(a) strictly increasing (0,π/2) (b) strictly decreasing in (π/2,π) (c) neither increasing nor decreasing in (0,π)
Solution :
Given:
The given function is
f
(
x
) = sin
x
.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.3
Question 4. Find the intervals in which the function F given by 2x 2 - 3x is (a) strictly increasing, (b) strictly decreasing. Solution : Given:
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.4
Question 5. Find the intervals in which the function F given by f ( x ) = 2 x 3 − 3 x 2 − 36 x + 7 is (a) strictly increasing, (b) strictly decreasing. Solution : (a)Given:.png)
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5
Question 6. Find the intervals in which the following functions are strictly increasing or decreasing:(a) x 2 + 2 x − 5 (b) 10 − 6 x − 2 x 2
(c) −2 x 3 − 9 x 2 − 12 x + 1 (d) 6 − 9 x − x 2
(e) ( x + 1) 3 ( x − 3) 3
Solution : (a) Given:
Question
7. Show that
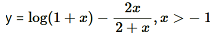is an increasing function of x throughout its domain.
Solution :
Given:
∴dydx=11+x-(2+x)(2)-2x(1)(2+x)2=11+x-4(2+x)2=x2(1+x)(2+x)2
Now, dydx=0
⇒x2(1+x)(2+x)2=0⇒x2=0 [(2+x)≠0 as x>-1]⇒x=0
Since x > -1 , point = 0 divides the domain (−1, ∞) in two disjoint intervals i.e., −1 < x < 0 and x > 0
When −1 < x < 0, we have:
x<0⇒x2>0x>-1⇒(2+x)>0⇒(2+x2)>0
∴ y'=x2(1+x)(2+x)2>0
Also, when x > 0
x>0⇒x2>0, (2+x)2>0
∴ y'=x2(1+x)(2+x)2>0
Hence, function f is increasing throughout this domain
Question
8. Find the value of x for which
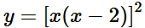is an increasing function.
Solution :
Question
9. Prove that
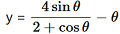is an increasing function of θ in [0, π/2]
Solution :
Question
10. Prove that the logarithmic function is strictly increasing on (0,∞)
Solution :
Given: The given function is f(x) = logx
∴ f'(x) = 1/x
It is clear that for x > 0, f'(x) = 1/x > 0.
Hence, f(x) = log x is strictly increasing in interval (0, ∞).
Question
11. Prove that the function f given by f (x) = x
2
- x + 1 is neither strictly increasing nor strictly decreasing on (-1,1)
Solution :
Given: The given function f (x) = x
2
- x + 1
hence,f is neither strictly increasing nor decreasing on the interval (-1,1)
Question
12. Which of the following functions are strictly decreasing on (0,π/2)
(A) cos x
(B) cos 2 x
(C) cos 3 x
(D) tan x
Solution :
Question
13. On which of the following intervals is the function f given by f(x) = x
100
+ sinx - 1 is strictly decreasing:
(A) (0, 1)
(B) (π/2,π)
(C) (0,π/2)
(D) None of these
Solution :
Given:
Question
14. Find the least value of a such that the function f given by f(x) = x
2
+ ax + 1 strictly increasing on (1, 2).
Solution :
Question
15. Let I be any interval disjoint from (-1,1) Prove that the function f given by f(x) = x + 1/x is strictly increasing on I.
Solution :
Given:
∴ f is strictly increasing on (-∞, 1) and (1, ∞)
Hence, function f is strictly increasing in interval I disjoint from (−1, 1).
Hence, the given result is proved.
Question
16. Prove that the function f given by f(x) = log sin x is strictly increasing on (0,π/2) and strictly decreasing on (π/2,π)
Solution :
Given:
Question
17. Prove that the function f given by f(x) = log cos x is strictly decreasing on (0,π/2) and strictly decreasing on (π/2,π)
Solution :
Given:
On the
Question
18. Prove that the function given by f(x) = x
3
- 3x
2
+ 3x - 100 is increasing in R.
Solution :
Given:
Question
19. The interval in which y = x
2
e
-x
is increasing in:
(A) (-∞, ∞)
(B)(-2,0)
(C) (2, ∞)
(D) (0, 2)
Solution :
Given:
NCERT Solutions For Class 12 Maths Chapter 6 Exercise 6.2 FAQs
How many exercise are there in application of derivatives?
Class 12 Maths Chapter 6 Application of Derivatives has 102 questions in 6 exercises along with 24 more provided in a miscellaneous exercise.
What are the applications of derivatives?
To calculate the profit and loss in business using graphs.
Who invented application of derivatives?
Calculus was discovered by Isaac Newton and Gottfried Leibniz in 17th Century. But it was not possible without the early developments of Isaac Barrow about the derivatives in 16th century.
What is sin differentiated?
For example, the derivative of the trigonometric function sin x is denoted as sin' (x) = cos x, it is the rate of change of the function sin x at a specific angle x is stated by the cosine of that particular angle. (i.e) The derivative of sin x is cos x.
What is dt in math?
Similarly, "dt" represents an infinitesimally small change in the independent variable t.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
