NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2 (Limits and Derivatives)
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2 contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in exercise 13.2.
Krati Saraswat19 Feb, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2 (Limits and Derivatives)
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2 Limits and Derivatives is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of chapter 13. Given Below is step-by-step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2 Limits and Derivatives.NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2 Overview
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2 cover several important topics. It is highly recommended for students to review each topic thoroughly in order to gain a comprehensive understanding of the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the result of dedicated efforts by the Physics Wallah teachers aimed at assisting students in grasping the concepts covered in this chapter. By going through and practicing these solutions, the objective is for students to achieve excellent results in their exams effortlessly.NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2
Question 1. If P (A) = 3/5 and P (B) = 1/5 find P (A ∩ B) if A and B are independent events. Solution : It is given that P(A) = 3/5 and P(B) = 1/5 As A and B are independent events. P (A ∩ B) = P(A) .P(B) = 3/5.1/5 = 3/25NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4
Question 2. Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black. Solution : There are 26 black cards in a deck of 52 cards. Let P (A) be the probability of getting a black card in the first draw. P(A) = 26/52 = 1/2 Let P (B) be the probability of getting a black card on the second draw. Since the card is not replaced, P(B) = 25/51 Thus, probability of getting both the cards black = 1/2 x25/51 = 25/102NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3
Question 3. A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale otherwise it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale. Solution: Let A, B, and C be the respective events that the first, second, and third drawn orange is good. Therefore, probability that first drawn orange is good, P (A) = 12/15 The oranges are not replaced. Therefore, probability of getting second orange good, P (B) = 11/14 Similarly, probability of getting third orange good, P(C) = 10/13 The box is approved for sale, if all the three oranges are good. Thus, probability of getting all the oranges good = 12/15 x 11/14 x 10/13 = 44/91 Therefore, the probability that the box is approved for sale is 44/91.NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.1
Question 4. A fair coin and an unbiased die are tossed. Let A be the event ‘head appears on the coin’ and B be the event ‘3 on the die’. Check whether A and B are independent events or not. Solution: If a fair coin and an unbiased die are tossed, then the sample space S is given by, S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)} Let A: Head appears on the coin
Therefore, A and B are independent events.
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.5
Question 5. A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event ‘number is even’ and B be the event ‘number is red’. Are A and B independent? Solution: When a die is thrown, the sample space (S) is S = {1, 2, 3, 4, 5, 6} Let A: the number is even = {2, 4, 6} P (A) = 3/6 = 1/2 B: the number is red = {1, 2, 3} P (B) = 3/6 = 1/2 ∴ A ∩ B = {2}
Therefore, A and B are not independent.
Question
6. Let E and F be events with
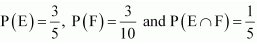Are E and F independent?
Solution:
Therefore, E and F are not independent events.
Question
7. Given that the events A and B are such that P (A) = 1/2 P (A ∩ B) = 3/5 and P (B) = p Find p if they are (i) mutually exclusive, (ii) independent.
Solution:
It is given that P(A) = 1/2 P (A ∩ B) = 3/5 and P (B) = p
(i) When A and B are mutually exclusive, A ∩ B =
Φ
∴ P (A ∩ B) = 0
It is known that P(A U B) = P(A) + P(B) - P(A ∩ B)
(ii) When A and B are independent, P(A ∩ B) = P(A) .P(B) = 1/2p
It is known that, P (A U B) = P(A) + P(B) - P(A ∩ B)
Question
8. Let A and B independent events, P (A) = 0.3 and P (B) = 0.4. Find:
(A) P (A ∩ B)
(B) P (A U B)
(C) P (A|B)
(D) P (B|A)
Solution :
P (A) = 0.3, P (B) = 0.4
A and B are independent events.
(i) P (A ∩ B) P (A). P (B) = 0.3 x 0.4 = 0.12
(ii) P (A U B) = P (A) + P (B) – P (A). P (B) = 0.03 + 0.4 – 0.3 x 0.4 = 0.7 – 0.12 = 0.58
(iii) P (A|B) = P (A ∩ B)/P(B) = P (A|B) = P (A) = 0.3
(iv) P
(B|A) = P (A ∩ B)/P(A) = P
(B|A) = P (B) = 0.4
Question
9. If A and B are two events such that P (A) = 1/4 P (B) = 1/2 and P (A ∩ B) = 1/8 find P (not A and not B).
Solution:
It is given that, P (A) = 1/4 and P (A ∩ B) = 1/8
P(not on A and not on B) =P(A' ∩ B')
P (not on A and not on B) P(A U B)' [A' ∩ B' = (A U B)']
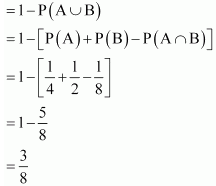
Question
10. Events A and B are such that P (A) = 1/2 P (B) = 7/12 and P (not A or not B) = 1/4 State whether A and B are independent.
Solution:
It is given that P (A) = 1/2 P (B) = 7/12 and P (not A or not B) = 1/4
Question
11. Given two independent events A and B such that P (A) = 0.3, P (B) = 0.6. Find:
(A) P (A and B)
(B) P (A and not B)
(C) P (A or B)
(D) P (neither A nor B)
Solution:
P (A) = 0.3, P (B) = 0.6
A and B are independent events.
(i) P (A and B) = P (A). P (B) = 0.3 x 0.6 = 0.18
(ii) P (A and not B) = P(A ∩ B') = P (A) – P(A ∩ B) = 0.3 – 0.18 = 0.12
(iii) P (A or B) = P (A) + P (B) – P (A and B) = 0.3 + 0.6 – 0.18 = 0.9 – 0.18 = 0.72
(iv) P (neither A nor B) = P(A' ∩ B') = (P(A U B')) 1 – P (A U B) = 1 – 0.72 = 0.28
Question
12. A die is tossed thrice. Find the probability of getting an odd number at least once.
Solution:
Probability of getting an odd number in a single throw of a die = 3/6 = 1/2
Similarly, probability of getting an even number =3/6 = 1/2
Probability of getting an even number three times = 1/2 x 1/2 x 1/2 = 1/8
Therefore, probability of getting an odd number at least once
= 1 − Probability of getting an odd number in none of the throws
= 1 − Probability of getting an even number thrice
= 1- 1/8 = 7/8
Question
13. Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that:
(i) both balls are red.
(ii) first ball is black and second is red.
(iii) one of them is black and other is red.
Solution :
Total number of balls = 18
Number of red balls = 8
Number of black balls = 10
(i) Probability of getting a red ball in the first draw = 8/18 = 4/9
The ball is replaced after the first draw.
∴ Probability of getting a red ball in the second draw = 8/18 = 4/9
Therefore, probability of getting both the balls red = 4/9 x 4/9 = 16/81
(ii) Probability of getting first ball black =10/18 = 5/9
The ball is replaced after the first draw.
Probability of getting second ball as red = 8/18 = 4/9
Therefore, probability of getting first ball as black and second ball as red =5/9 x 4/9 = 20/81
(iii) Probability of getting first ball as red =8/18 = 4/9
The ball is replaced after the first draw.
Probability of getting second ball as black =10/18 = 5/9
Therefore, probability of getting first ball as black and second ball as red = 4/9 x 5/9 = 20/81
Therefore, probability that one of them is black and other is red
= Probability of getting first ball black and second as red + Probability of getting first ball red and second ball black
= 20/81 + 20/81 = 40/81
Question
14. Probability of solving specific problem independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem independently, find the probability that:
(i) the problem is solved.
(ii) exactly one of them solves the problem.
Solution :
Probability of solving the problem by A, P (A) =1/2
Probability of solving the problem by B, P (B) =1/3
Since the problem is solved independently by A and B,
∴ P(AB) = P(A).P(B) = 1/2 x 1/3 = 1/6
P(A') = 1 - P(A) = 1-1/2 = 1/2
P(B') = 1 - P(B) = 1 - 1/3 = 2/3
(i)Probability that the problem is solved = P (A ∪ B)
= P (A) + P (B) − P (AB) = 1/2 + 1/3 -1/6 = 4/6 = 2/3
(ii) Probability that exactly one of them solves the problem is given by, P(A).P(B') + P(B).P(A')
= 1/2 x 2/3 + 1/2 x 1/3 = 1/3 + 1/6 = 1/2
Question
15. One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events E and F independent?
Solution :
(i) In a deck of 52 cards, 13 cards are spades and 4 cards are aces.
∴ P(E) = P(the card drawn is a spade) =13/52 = 1/4
∴ P(F) = P(the card drawn is an ace) = 4/52 = 1/13
In the deck of cards, only 1 card is an ace of spades.
P(EF) = P(the card drawn is spade and an ace) = 1/52
P(E) × P(F) =1/4 .1/12 = 1/52 = P(EF)
⇒ P(E) × P(F) = P(EF)
Therefore, the events E and F are independent.
(ii) In a deck of 52 cards, 26 cards are black and 4 cards are kings.
∴ P(E) = P(the card drawn is black) = 26/52 = 1/2
∴ P(F) = P(the card drawn is a king) = 4/52 = 1/13
In the pack of 52 cards, 2 cards are black as well as kings.
∴ P (EF) = P(the card drawn is a black king) =2/52 = 1/26
P(E) × P(F) = 1/2.1/13 = 1/26 =P(EF)
Therefore, the given events E and F are independent.
(iii) In a deck of 52 cards, 4 cards are kings, 4 cards are queens, and 4 cards are jacks.
∴ P(E) = P(the card drawn is a king or a queen) = 8/52 = 2/13
∴ P(F) = P(the card drawn is a queen or a jack) = 8/52 = 2/13
There are 4 cards which are king or queen and queen or jack.
∴ P(EF) = P(the card drawn is a king or a queen, or queen or a jack)
=4/52 = 1/13
P(E) × P(F) =-2/13.2/13 = 4/169 ≠ 1/13
⇒ P(E) .P(F) ≠ P(EF)
Therefore, the given events E and F are not independent.
Question
16. In a hostel 60% of the students read Hindi newspaper, 40% read English newspaper and 20% read both Hindi and English newspapers. A student is selected at random.
(a) Find the probability that she reads neither Hindi nor English newspapers.
(b) If she reads Hindi newspaper, find the probability that she reads English newspaper.
(c) If she reads English newspapers, find the probability she reads Hindi newspaper.
Solution :
Let H denote the students who read Hindi newspaper and E denote the students who read English newspaper.
It is given that,
(i) Probability that a student reads Hindi or English newspaper is
(ii) Probability that a randomly chosen student reads English newspaper, if she reads Hindi news paper, is given by P (E|H).
(iii) Probability that a randomly chosen student reads Hindi newspaper, if she reads English newspaper, is given by P (H|E).
Choose the correct answer in the following:
Question 17. The probability of obtaining an even prime number on each die when a pair of dice is rolled is: (A) 0 (B) 1/3 (C) 1/12 (D) 1/36 Solution : When two dice are rolled, the number of outcomes is 36. The only even prime number is 2. Let E be the event of getting an even prime number on each die. ∴ E = {(2, 2)} ⇒ P(E) = 1/36 Hence option (D) is correct. Question 18. Two events A and B are said to be independent, if: (A) A and B are mutually exclusive. (B) P (A’B’) = [1 – P (A)] [1 – P (B)] (C) P (A) = P (B) (D) P (A) + P (B) = 1 Solution : P (A’ and B’) = [1 – P (A)] . [1 – P (B)] = P (A’). P (B’) Hence, option (B) is correctNCERT Solutions For Class 12 Maths Chapter 13 Exercise 13.2 FAQs
What is the hardest chapter in math class 12?
The hardest chapter is integrals for most of them.
What is a derivative as a rate measure?
If a quantity y is dependent on and varies in relation to a quantity x, then the rate of change of y with respect to x is denoted by the symbol dy/dx (difference between two numbers).
What are the applications of derivatives?
To calculate the profit and loss in business using graphs.
Which is the most important chapter in maths class 12?
CBSE Class 12 Maths must be studied smartly. Students must give priority to those chapters primarily that consist of major weightage of marks. Algebra, Calculus, Vectors, and Three-Dimensional Geometry are the most vital chapters from this perspective.
Why derivative is called rate of change?
The derivative of a given function y=f(x) y = f ( x ) measures the instantaneous rate of change of the output variable with respect to the input variable.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.