
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1 (Applications of Derivatives)
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1 Applications of Derivatives is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 6. Given below is step by step solutions of all questions given in the NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1.NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1 (Applications of Derivatives) Overview
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1 is prepared by our experts to help students understand the concepts of the chapter better. Students can solve these questions before their examinations these questions will help them to understand the concepts better and by doing these questions students can easily ace their examinations.NCERT Solutions for Class 12 Maths Exercise 6.1
Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1:
Question 1. Find the rate of change of the area of a circle with respect to its radius r when (a)r = 3 cm (b)r = 4 cm Solution : The area of a circle (A) with radius (r) is given by, A = πr 2 Now, the rate of change of the area with respect to its radius is given by, = (a) When r = 3 cm, then
(a) When r = 3 cm, then
 sq. cm
(b) When r = 4 cm, then
sq. cm
(b) When r = 4 cm, then
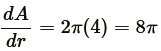 sq. cm
sq. cm
NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
Question 2. The volume of a cube is increasing at the rate of 8 cm3/sec. How fast is the surface area increasing when the length of an edge is 12 cm? Solution : Let x be the length of a side, V be the volume, and s be the surface area of the cube. Given: Rate of increase of volume of cube = 8 cm3/sec Then, V = x 3 and S = 6 x 2 where x is a function of time t It is given tha
 Hence, if the length of the edge of the cube is 12 cm, then the surface area is increasing at the rate of 8/3 cm
2
/s.
Hence, if the length of the edge of the cube is 12 cm, then the surface area is increasing at the rate of 8/3 cm
2
/s.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2
Question 3. The radius of the circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm. Solution : The area of a circle ( A) with radius (r ) is given by, A = πr 2 Now, the rate of change of the area with respect to its radius is given by, = It is given that,
It is given that,
 Hence, the rate at which the area of the circle is increasing when the radius is 10 cm is 60π cm
2
/s.
Hence, the rate at which the area of the circle is increasing when the radius is 10 cm is 60π cm
2
/s.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.3
Question 4. An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge if 10 cm long? Solution : Let x be the length of a side and V be the volume of the cube. Then, V = x 3. Hence, the volume of the cube is increasing at the rate of 900 cm
3
/s when the edge is 10 cm long.
Hence, the volume of the cube is increasing at the rate of 900 cm
3
/s when the edge is 10 cm long.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.4
Question 5. A stone is dropped into a quite lake and waves move in circles at the rate of 5 cm/sec. At the instant when radius of the circular wave is 8 cm, how fast is the enclosed area increasing? Solution: The area of a circle ( A ) with radius ( r ) is given by A = πr 2 Therefore, the rate of change of area ( A) with respect to time ( t) is given by, Hence, when the radius of the circular wave is 8 cm, the enclosed area is increasing at the rate of 80π cm
2
/s.
Hence, when the radius of the circular wave is 8 cm, the enclosed area is increasing at the rate of 80π cm
2
/s.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5
Question 6. The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of its circumference? Solution : The circumference of a circle ( C ) with radius ( r) is given by C = 2π r. Therefore, the rate of change of circumference (C) with respect to time ( t) is given by, Hence, the rate of increase of the circumference is 2π(0.7) = 1.4π cm/s
Question
7. The length x of a rectangle is decreasing at the rate of 5 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter and (b) the area of the rectangle.
Solution :
Since the length (
x)
is decreasing at the rate of 5 cm/minute and the width (
y)
is increasing at the rate of 4 cm/minute, we have:
Hence, the rate of increase of the circumference is 2π(0.7) = 1.4π cm/s
Question
7. The length x of a rectangle is decreasing at the rate of 5 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter and (b) the area of the rectangle.
Solution :
Since the length (
x)
is decreasing at the rate of 5 cm/minute and the width (
y)
is increasing at the rate of 4 cm/minute, we have:
 Hence, the area of the rectangle is increasing at the rate of 2 cm
2
/min.
Question
8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimeters of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
Solution :
The volume of a sphere (
V)
with radius (
r
) is given by,
V = 4/3πr
3
∴Rate of change of volume (
V)
with respect to time (
t)
is given by,
Hence, the area of the rectangle is increasing at the rate of 2 cm
2
/min.
Question
8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimeters of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
Solution :
The volume of a sphere (
V)
with radius (
r
) is given by,
V = 4/3πr
3
∴Rate of change of volume (
V)
with respect to time (
t)
is given by,
 Hence, the rate at which the radius of the balloon increases when the radius is 15 cm is 1/π cm/s.
Question
9. A balloon, which always remains spherical has a variables radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
Solution :
Since, V = 4/3πr
3
Rate of change of volume (
V)
with respect to its radius (
r)
is given by,
Hence, the rate at which the radius of the balloon increases when the radius is 15 cm is 1/π cm/s.
Question
9. A balloon, which always remains spherical has a variables radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
Solution :
Since, V = 4/3πr
3
Rate of change of volume (
V)
with respect to its radius (
r)
is given by,
 Hence, the volume of the balloon is increasing at the rate of 400π cm
2
.
Question
10. A ladder 5 cm long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
Solution :
Let
y
m be the height of the wall at which the ladder touches. Also, let the foot of the ladder be
x
maway from the wall.
Then, by Pythagoras theorem, we have:
x
2
+
y
2
= 25 [Length of the ladder = 5 m]
⇒ y = √25 - x
2
Then, the rate of change of height (
y)
with respect to time (
t)
is given by,
Hence, the volume of the balloon is increasing at the rate of 400π cm
2
.
Question
10. A ladder 5 cm long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
Solution :
Let
y
m be the height of the wall at which the ladder touches. Also, let the foot of the ladder be
x
maway from the wall.
Then, by Pythagoras theorem, we have:
x
2
+
y
2
= 25 [Length of the ladder = 5 m]
⇒ y = √25 - x
2
Then, the rate of change of height (
y)
with respect to time (
t)
is given by,
 Hence, the height of the ladder on the wall is decreasing at the rate of 8/3 cm/s.
Question
11. A particle moves along the curve 6y = x
3
+ 2 Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.
Solution :
Given: Equation of the curve 6y = x
3
+ 2……….(i)
The rate of change of the position of the particle with respect to time (
t)
is given by,
Hence, the height of the ladder on the wall is decreasing at the rate of 8/3 cm/s.
Question
11. A particle moves along the curve 6y = x
3
+ 2 Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.
Solution :
Given: Equation of the curve 6y = x
3
+ 2……….(i)
The rate of change of the position of the particle with respect to time (
t)
is given by,
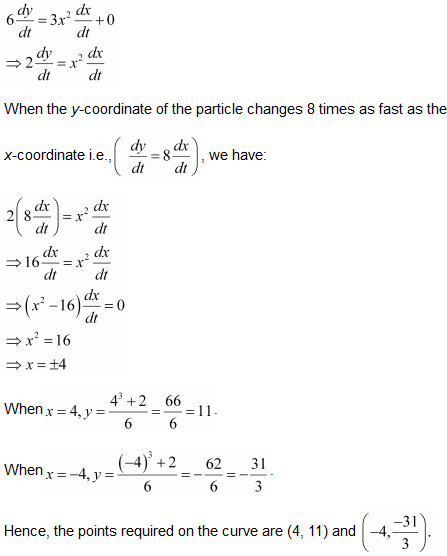 Question
12. The radius of an air bubble is increasing at the rate of 1/2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Solution :
The air bubble is in the shape of a sphere.
Now, the volume of an air bubble (
V
) with radius (
r
) is given by,
V = 4/3πr
3
The rate of change of volume (
V)
with respect to time (
t)
is given by,
Question
12. The radius of an air bubble is increasing at the rate of 1/2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Solution :
The air bubble is in the shape of a sphere.
Now, the volume of an air bubble (
V
) with radius (
r
) is given by,
V = 4/3πr
3
The rate of change of volume (
V)
with respect to time (
t)
is given by,
 Hence, the rate at which the volume of the bubble increases is 2π cm
3
/s.
Question
13. A balloon which always remains spherical, has a variable diameter 3/2 (2x + 1) Find the rate of change of its volume with respect to x
Solution :
The volume of a sphere (
V
) with radius (
r
) is given by,
V = 4/3πr
3
It is given that:
Diameter 3/2 (2x + 1)
Hence, the rate at which the volume of the bubble increases is 2π cm
3
/s.
Question
13. A balloon which always remains spherical, has a variable diameter 3/2 (2x + 1) Find the rate of change of its volume with respect to x
Solution :
The volume of a sphere (
V
) with radius (
r
) is given by,
V = 4/3πr
3
It is given that:
Diameter 3/2 (2x + 1)
 Question
14. Sand is pouring from a pipe at the rate of 12 cm
3
/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4cm?
Solution :
The volume of a cone (
V)
with radius (
r
) and height (
h)
is given by,
V = 4/3πr
3
It is given that,
h = 1/6r ⇒r = 6h
Question
14. Sand is pouring from a pipe at the rate of 12 cm
3
/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4cm?
Solution :
The volume of a cone (
V)
with radius (
r
) and height (
h)
is given by,
V = 4/3πr
3
It is given that,
h = 1/6r ⇒r = 6h
 Hence, when the height of the sand cone is 4 cm, its height is increasing at the rate of 1/48π cm/s.
Question
15. The total cost C(x) in rupees associated with the production of x units of an item given by
Hence, when the height of the sand cone is 4 cm, its height is increasing at the rate of 1/48π cm/s.
Question
15. The total cost C(x) in rupees associated with the production of x units of an item given by
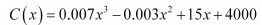 Find the marginal cost when 17 units are produced.
Solution :
Marginal cost is the rate of change of total cost with respect to output.
Find the marginal cost when 17 units are produced.
Solution :
Marginal cost is the rate of change of total cost with respect to output.
 Hence, when 17 units are produced, the marginal cost is Rs. 20.967.
Question
16. The total revenue in rupees received from the sale of x units of a product is given by
Hence, when 17 units are produced, the marginal cost is Rs. 20.967.
Question
16. The total revenue in rupees received from the sale of x units of a product is given by
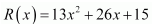 Find the marginal revenue when x = 7
Solution :
Marginal Revenue (MR) =
Find the marginal revenue when x = 7
Solution :
Marginal Revenue (MR) =
 When
x
= 7,
MR = 26(7) + 26 = 182 + 26 = 208
Hence, the required marginal revenue is Rs 208.
When
x
= 7,
MR = 26(7) + 26 = 182 + 26 = 208
Hence, the required marginal revenue is Rs 208.
Choose the correct answer in Exercises 17 and 18.
Question 17. The rate of change of the area of a circle with respect to its radius r at r = 6 cm is(A) 10π
(B) 12π
(C) 8π
(D) 11π
Solution : The area of a circle ( A) with radius ( r ) is given by, A = πr 2 Therefore, the rate of change of the area with respect to its radius r is Hence, the required rate of change of the area of a circle is 12π cm
2
/s.
The correct answer is B.
Question
18. The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 3x
2
+ 36x + 5 The marginal revenue, when x = 15 is:
(A) 116
(B) 96
(C) 90
(D) 126
Solution :
Marginal revenue is the rate of change of total revenue with respect to the number of units sold.
∴Marginal Revenue (MR)= dR/dx= 3(2
x
) + 36 = 6
x
+ 36
∴When
x
= 15,
MR = 6(15) + 36 = 90 + 36 = 126
Hence, the required marginal revenue is Rs 126.
The correct answer is D.
Hence, the required rate of change of the area of a circle is 12π cm
2
/s.
The correct answer is B.
Question
18. The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 3x
2
+ 36x + 5 The marginal revenue, when x = 15 is:
(A) 116
(B) 96
(C) 90
(D) 126
Solution :
Marginal revenue is the rate of change of total revenue with respect to the number of units sold.
∴Marginal Revenue (MR)= dR/dx= 3(2
x
) + 36 = 6
x
+ 36
∴When
x
= 15,
MR = 6(15) + 36 = 90 + 36 = 126
Hence, the required marginal revenue is Rs 126.
The correct answer is D.
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1 FAQs
What is Chapter 6 of Class 12 Maths about?
Chapter 6 of Class 12 Maths is titled "Applications of Derivatives." It deals with various real-life applications of derivatives, such as rate of change, increasing and decreasing functions, tangents and normals, and maxima and minima.
What is Exercise 6.1 about?
Exercise 6.1 focuses on finding the rate of change of quantities using derivatives. It includes problems related to finding the rate of change of area, volume, etc., with respect to time.
Why is it important to study Applications of Derivatives in Class 12 Maths?
Applications of Derivatives are crucial as they help in understanding how derivatives are used to analyze real-world problems. These applications are common in physics, economics, biology, and various other fields.
How can NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1 help students?
NCERT Solutions provide step-by-step explanations for each problem in Exercise 6.1. They help students understand the concepts thoroughly and serve as a valuable resource for self-assessment.
Where can I find NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1?
NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.1 can be found in the official NCERT textbooks.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App









