
The percent difference formula determines the absolute value of the change in value between two numbers in the same category. It involves computing the absolute value of the ratio of their difference to their average, then multiplying the result by 100. This formula helps calculate and apply the percentage difference between two figures.
What is the Percent Difference Formula?
The percent difference formula computes the disparity between two numbers in percentage form. It derives this percentage by evaluating the ratio of the numerical difference between the values to their average, all multiplied by 100.
Characteristics:
It quantifies the change in value relative to 100.
It gauges the absolute variance between two quantities.
The value is consistently positive.
It is a dimensionless measurement.
Formula:
Percentage difference = (Absolute difference / Average) × 100
Explanation: Assuming the initial value is 'a' and the final value is 'b'.
Hence, the average value is calculated as (a + b) / 2.
The difference between the values is represented as (b – a).
The absolute value of this difference is |b – a|.
Hence, the ratio becomes |b – a| / ((a + b) / 2) = 2|b – a| / (b + a).
Thus, the percentage difference formula is expressed as:
2|b – a| / (b + a) × 100.
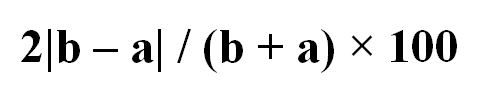
Percent Difference Formula Solved Examples
Example 1: Calculate the percentage difference between 80 and 120.
Solution:
Average value = (80 + 120) / 2 = 200 / 2 = 100
Absolute difference = |120 - 80| = 40
Hence, percentage difference = (40 / 100) × 100 = 40%
Example 2: Given the initial value of an investment as $500 and the final value as $700, find the percentage difference in investment value.
Solution:
Average investment value = ($500 + $700) / 2 = $1200 / 2 = $600
Absolute difference in values = |$700 - $500| = $200
Therefore, the percentage difference = ($200 / $600) × 100 = 33.33%
Example 3: Determine the other value if one value is 150 and the percentage difference is 25%.
Solution:
Let the other value be 'a'.
Given: one value is 150 and the percentage difference is 25%.
The average value is (a + 150) / 2.
The absolute difference = |150 - a|
The percentage difference is |150 - a| / ((a + 150) / 2) = 2|150 - a| / (a + 150) × 100
Thus, the equation is: 2|150 - a| / (a + 150) × 100 = 25
This simplifies to: |150 - a| / (a + 150) = 0.25
Two possible cases arise:
Case 1: If a > 150,
Then, |150 - a| = a - 150
(a - 150) / (a + 150) = 0.25
Solving for 'a':
a - 150 = 0.25a + 37.5
a - 0.25a = 187.5
0.75a = 187.5
a = 250
Case 2: If a < 150,
Then, |150 - a| = 150 - a
(150 - a) / (a + 150) = 0.25
Solving for 'a':
150 - a = 0.25a + 37.5
a + 0.25a = 112.5
1.25a = 112.5
a = 90
Example 4: Find the percentage difference between 35 and 50.
Solution:
Determine the average value:
Average = (35 + 50) / 2
= 85 / 2
= 42.5
Calculate the absolute difference:
Absolute difference = |50 - 35|
= 15
Find the percentage difference:
Percentage difference = (15 / 42.5) × 100
≈ 0.3529 × 100
≈ 35.29%
Therefore, the percentage difference between 35 and 50 is approximately 35.29%.
The percent difference formula serves as a valuable tool for assessing the relative change between two values within the same category. It measures this change in percentage form, allowing for a standardized comparison across various numerical ranges. By determining the absolute value of the difference between two figures relative to their average, multiplied by 100, the formula provides a clear and standardized measure of the disparity.
Key characteristics of the percent difference formula include its representation of change relative to 100, its ability to measure absolute variance between values, its consistent positive output, and its status as a dimensionless measurement.
Understanding and applying this formula involves calculating the average value of the numbers, finding their difference, taking the absolute value of the difference, and then applying the formula:
Percentage difference =2×∣b−a∣/(b+a)×100
Percentage difference=2×∣b−a∣/(b+a)×100, where 'a' and 'b' represent the initial and final values, respectively.
Multiple examples have been provided to demonstrate the practical application of this formula in different scenarios, ranging from numerical calculations to finding unknown values when the percentage difference and one value are given.
The percent difference formula offers a standardized and easily interpretable means to assess the relative change between two values, proving invaluable in various fields such as finance, economics, science, and everyday quantitative analyses.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| T-Test Formula | Trajectory Formula |
| U Substitution Formula | Vertex Formula |
Percent Difference Formula FAQs
What is the Percent Difference Formula?
How is the formula represented?
What are the characteristics of the formula?
In what fields is the formula commonly used?










