
Root Mean Square Formula: The root mean square formula is used to determine the square root of the total sum of squares of individual data points in an observation. It is known as RMS, it represents the square root of the average of the squared values within a dataset, also known as the quadratic mean. This RMS value can be extended to continuously varying functions by defining it in relation to the integral of the squares of instantaneous values throughout a cycle. In this context, the root mean square formula computes the square root of the average of the function's squares, defining the continuous waveform.
What is Root Mean Square Formula
Formula 1 In a dataset comprising "n" values represented by = x 1 ,x 2 ,x 3 ,…,x n , the root mean square formula is expressed as:
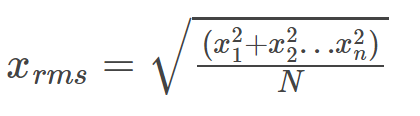
Formula 2 Expressing the root mean square formula for a continuous function f(t) defined within the interval T 1 ≤t≤T 2 , it is given as:
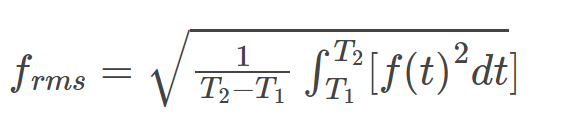
Root Mean Square Formula Solved Examples
Example 1 : Calculate the root mean square of the following observations: 6, 5, 4, 2, 8?
Solution: To find: Root mean square of the given observations.
Using the root mean square formula,
X r m s = √ x 1 2 + x 2 2 + x 3 2 + . . . + x n 2 / n
= (√ 6 2 + 5 2 + 4 2 + 3 2 + 8 2 )/ 5 = 5.196
Answer: The root mean square of the given values is approximately 5.196.
Example 2 : Calculate the root mean square of the following observations: 3, 8, 12, 4, 9?
Solution: To find: Root mean square of the given observations.
Using the root mean square formula,
X r m s = √ x 1 2 + x 2 2 + x 3 2 + . . . + x n 2 / n
= (√ 3 2 + 8 2 + 12 2 + 4 2 + 9 2 )/5 = 7.92
Answer: The root mean square of the given values is approximately 7.92.
Example 3 : Calculate the root mean square of the following observations: 1, 1, 1, 1, 1?
Solution: To find: Root mean square of the given observations.
Using the root mean square formula,
X r m s = √ x 1 2 + x 2 2 + x 3 2 + . . . + x n 2 / n
(√ 1 2 + 1 2 + 1 2 + 1 2 + 1 2 )/5 = 1
Answer: The root mean square of the given values is approximately 1.
Example 4 : Calculate the root mean square of the following observations: 0, 4, 6, 8, 10?
Solution: To find: Root mean square of the given observations.
Using the root mean square formula,
X r m s = √ x 1 2 + x 2 2 + x 3 2 + . . . + x n 2 / n
(√ 0 2 + 4 2 + 6 2 + 8 2 + 10 2 ) /5 = 6.57
Answer: The root mean square of the given values is approximately 6.57.
Example 5 :Determine the root mean square value of f(t)=t within the interval 2≤t≤5.
Solution: The objective is to find the root mean square value of f(t)=t over the interval 2≤t≤5.
Using the root mean square value formula for the given function f(t),
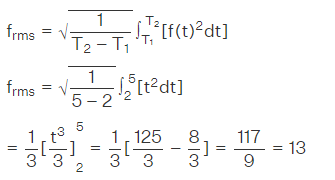
Root Mean Square (RMS) formula serves as a valuable method for determining the square root of the total sum of squares in a dataset, whether composed of discrete values or continuous functions within a specified interval. It calculates the square root of the average of the squared values, representing a measure of the effective magnitude or power in a set of observations.
This mathematical approach, applicable to various fields such as engineering, physics, statistics, and signal processing, provides a reliable way to gauge the magnitude of variability or the "effective" value within a dataset. Whether applied to discrete data points or continuous functions, the RMS formula offers a standardized metric for analyzing the underlying trends or properties of a dataset, offering insights into its characteristics.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Function Notation Formula | Hexagonal Pyramid Formula |
| Hypothesis Testing Formula | Interquartile Range Formula |
Root Mean Square Formula FAQs
What is the Root Mean Square (RMS) formula?
What does RMS represent in a dataset?
What's the significance of the RMS formula?
How is RMS used in electricity or signal analysis?










