Statistics Formula: The field of Statistics is concerned with the exploration of data through processes involving its collection, analysis, interpretation, presentation, and organization. In this realm, statistics formulas play a crucial role, facilitating the examination of data, the comprehension of outcomes, and the formulation of assumptions about potential outcomes. Let's delve into the fundamental statistics formulas, along with illustrative examples to enhance understanding.
Also Check -
Factorization Formula
What are the Statistics Formulas?
Fundamental statistics formulas prove invaluable in the interpretation of numerical data, enabling us to decipher facts and information presented in numeric form. These formulas empower us to compute diverse measures of central tendencies and assess the dispersion or variation of data points from the central value. Presented below are significant statistics formulas:
Mean Median Mode
The formulas for mean, median, and mode aid us in determining measures of central tendency. These measures provide insight into the typical or central value within a dataset. Both for grouped and ungrouped data, we employ the following formulas to compute the mean, median, and mode:
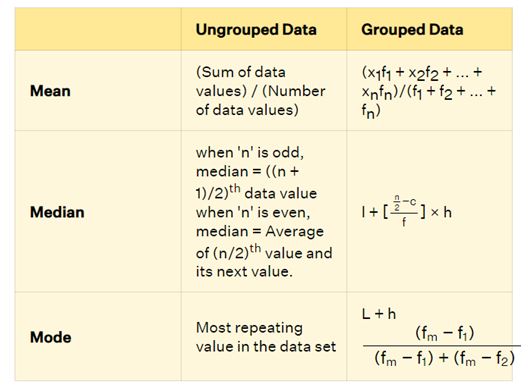
What is the Mean Median Mode Formula?
To begin, let's clarify the meanings of mean, median, and mode in the realm of statistics.
-
Mean, also referred to as the arithmetic mean, signifies the average value within the provided dataset.
-
Median denotes the middlemost value within a set of ungrouped data when arranged in ascending order.
-
Mode represents the value that appears most frequently in the dataset
Download PDF Statistics Formula
The formulas for calculating the mean, median, and mode for grouped data are detailed below individually.
Mean Formula
The formula for the mean of ungrouped data involves adding up all the observations and then dividing by the total count of observations. This formula is a foundational tool for solving various concepts related to the arithmetic mean. The formula for the mean of given observations is as follows:
Mean Formula = (Sum of Observations) ÷ (Total Number of Observations)
Similarly, for grouped data, there exists a mean formula expressed as:
Where
:
x̄ = Σ f x /n
x represents the midpoint of each class.
f stands for the frequency of the respective class.
n denotes the total frequency.
In essence, the mean represents the average value derived from all data points.
Also Check -
Line and Angles Formula
Median Formula
To determine the median of ungrouped data, it's essential to arrange the data either in ascending or descending order. Once the data is organized, calculate the total number of observations within the dataset.
If the count of observations is odd, the median corresponds to the ((n+1)/2)th item in the given set.
If the count of observations is even, identify the two middle terms, which are the (n/2)th and ((n/2) + 1)th values. Then, calculate the average of these two middle terms. The formula for the median in the case of even numbers is as follows: Median = ((n/2)th term + ((n/2) + 1)th term)/2
For grouped data, the median formula is outlined below. Initially, determine the median class, which is the class encompassing the ((n + 1)/2)th item.
Median = l + [(n/2−c)/f] × h
Where,
-
l denotes the lower limit of the median class.
-
n stands for the total frequency.
-
c represents the cumulative frequency of the class preceding the median class.
-
f signifies the frequency of the median class.
-
H indicates the class width (Upper limit - Lower limit).
Also Check -
Introduction to Graph Formula
Mode
In ungrouped data, the mode refers to the value or number that appears most frequently within the dataset. In situations where data contains no repeated values, every individual data point is considered a mode.
To calculate the mode for grouped data, you can employ the following mode formula. However, prior to using this formula, it's necessary to identify the modal class, which is the class with the highest frequency.
Mode formula = L + h (fm−f1)/(fm−f1)+(fm−f2)
-
L' signifies the lower limit of the modal class.
-
'h' represents the size of the class interval.
-
'fm’ denotes the frequency of the modal class.
-
'f1’ stands for the frequency of the class immediately preceding the modal class.
-
'f2’ indicates the frequency of the class immediately succeeding the modal class.
