
Summation Formula: Before discussing the summation formulas, let's refresh our understanding of summation. Summation, often referred to as the sum, represents the cumulative addition of consecutive terms within a sequence. Instead of manually writing out the total sum of 'n' terms in a sequence represented by {an}, we use summation notation, denoted as ∑ni=1ai, to compactly express this total. This notation condenses the expression a1 + a2 + ... + an into a concise format. Now, we'll explore various summation formulas and their practical applications through a series of solved examples.
Summation Formula
Summation formulas serve the purpose of determining the total sum within a sequence. These formulas cater to different types of sequences like arithmetic or geometric sequences, offering specific methods for their summation. Moreover, they include formulas designed to calculate various summations, such as the sum of natural numbers, squares, cubes, even numbers, odd numbers, and more. This comprehensive array of summation formulas will be further elaborated upon in the following section, examining each formula in detail.
List of Summation Formulas
The total sum of two numbers results from their addition. In a sequence represented by {x1, x2, ..., xn}, the collective sum of its elements is symbolized by Σ (sigma). For instance, the sum of the aforementioned sequence is expressed as ∑ni=1xi = x1 + x2 + ... + xn. In this context, ∑ni=1 denotes the summation of sequence terms from the first term to the nth term, articulated as "sigma i equals 1 to n." However, computing the sum of sequences manually each time can be laborious. Instead, we rely on specific summation formulas to facilitate this task. Presented below are some prevalent summation formulas.
Formulas for Calculating Sums
Sum of the first n natural numbers:
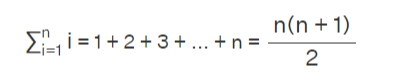
Sum of the squares of the first n natural numbers:
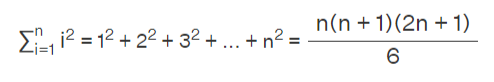
Sum of the cubes of the first n natural numbers:
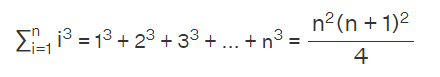
Sum of the fourth powers of the first n natural numbers:
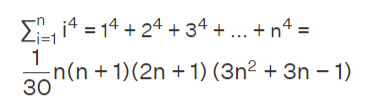
Sum of the first n even natural numbers:

Sum of the first n odd natural numbers:
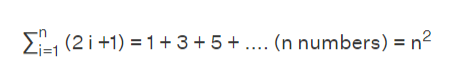
Sum of the arithmetic sequence
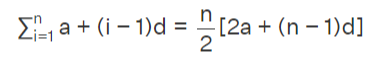
Sum of the geometric sequence a, ar, ar 2 ,...,ar n−1
Sum of the first n terms: 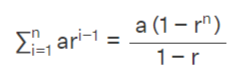
Sum of the infinite terms: 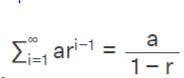
(only when ∣r∣<1)
Summation Formula Solved Examples
Example 1: Finding the sum of the first 20 natural numbers.
Solution: Given n=20, the sum of the first n natural numbers is:
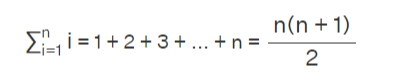
= 20(20+1) / 2
=210
Answer: The sum of the first 20 natural numbers is 210.
Example 2: Calculate the sum of the squares of the first 15 natural numbers.
Solution: For n=15, the sum of the squares of the first n natural numbers is given by:
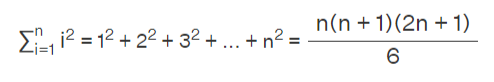
= 15(15+1)(2×15+1) / 6 =( 15 × 16 × 31)/ 6
=1240
Answer: The sum of the squares of the first 15 natural numbers is 1240.
Summation formulas are invaluable tools for swiftly calculating the cumulative sums of sequences without the need for manual computation. These formulas cater to various sequence types and provide specific methods for finding sums of natural numbers, squares, cubes, even and odd numbers, and more. By using concise notation and specific formulas, mathematicians and learners can efficiently determine sums, facilitating a deeper understanding of sequence properties and aiding in problem-solving across diverse mathematical contexts.
Understanding the fundamentals of summation not only involves recognizing the utility of compact notation (∑) but also the application of various formulas for specific sequences. The examples provided demonstrate the practical use of these formulas, showcasing how they streamline the calculation process for sums of varying sequence types.
By comprehending and utilizing summation formulas, mathematicians and learners gain a powerful toolset to analyze and compute sums, promoting efficiency and accuracy in calculations involving sequences, thus furthering their understanding and application of mathematical concepts.
| Related Links | |
| Hexagonal Pyramid Formula | Hypothesis Testing Formula |
| Interquartile Range Formula | Inverse Variation Formula |
Summation Formula FAQs
What is a summation formula?
Why are summation formulas useful?
What do summation formulas cover?
How are summation formulas represented?










