Physics Wallah

NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion

NCERT Solutions For Class 6 Maths Chapter 12 have been given below for the reference of CBSE Class 6 students. Students can check the complete NCERT Solutions for Class 6 Maths Chapter 12 here
authorImageJasdeep Bhatia12 Jan, 2024
Share

Share

NCERT Solutions for Class 6 Chapter 12

NCERT Solutions for Class 6 Maths Chapter 12

NCERT Solutions For Class 6 Maths Chapter 12: NCERT Solutions for Chapter 12 Ratio and Proportion in Class 6 Maths are now available on the official PhysicsWallah website. You can easily download the complete chapter and prepare for your Class 6 examination by solving Ratio and Proportion questions. The NCERT Class, 6 Maths solutions, are created by experienced teachers who effectively explain topics to children. These teachers have extensive experience and skills in teaching students, ensuring a quick understanding of the concepts in Chapter 12 of Class 6 Maths. If you have any questions, feel free to contact the experts on our PhysicsWallah website; they will provide the correct solutions to all your doubts. Access to NCERT solutions for Class 6 Science, Maths, English, Hindi, and other subjects will make studying these subjects easier.

NCERT Solutions for Class 6 Maths Chapter 12 PDF Download

NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion

NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion have been given below for your help! Keep on reading for the detailed solutions with easy-to-understand explanations that will help you with your preparation:

Exercise 12.1 Page No. 251

1. There are 20 girls and 15 boys in the class.

(a) What is the ratio of the number of girls to the number of boys? (b) What is the ratio of the number of girls to the total number of students in the class? Solutions: Given Number of girls = 20 girls Number of boys = 15 boys Total number of students = 20 + 15 = 35 (a) Ratio of the number of girls to the number of boys = 20 / 15 = 4 / 3 (b) Ratio of the number of girls to the total number of students = 20 / 35 = 4 / 7 2. Out of 30 students in a class, 6 like football, 12 like cricket and the remaining like tennis. Find the ratio of (a) The number of students liking football to the number of students liking tennis. (b) The number of students liking cricket is the total number of students. Solutions: Given Number of students who like football = 6 Number of students who like cricket = 12 Number of students who like tennis = 30 – 6 – 12 = 12 (a) Ratio of the number of students liking football to the number of students liking tennis = 6 / 12 = 1 / 2 (b) Ratio of the number of students liking cricket to the total number of students = 12 / 30 = 2 / 5

CBSE Admit Card 2024

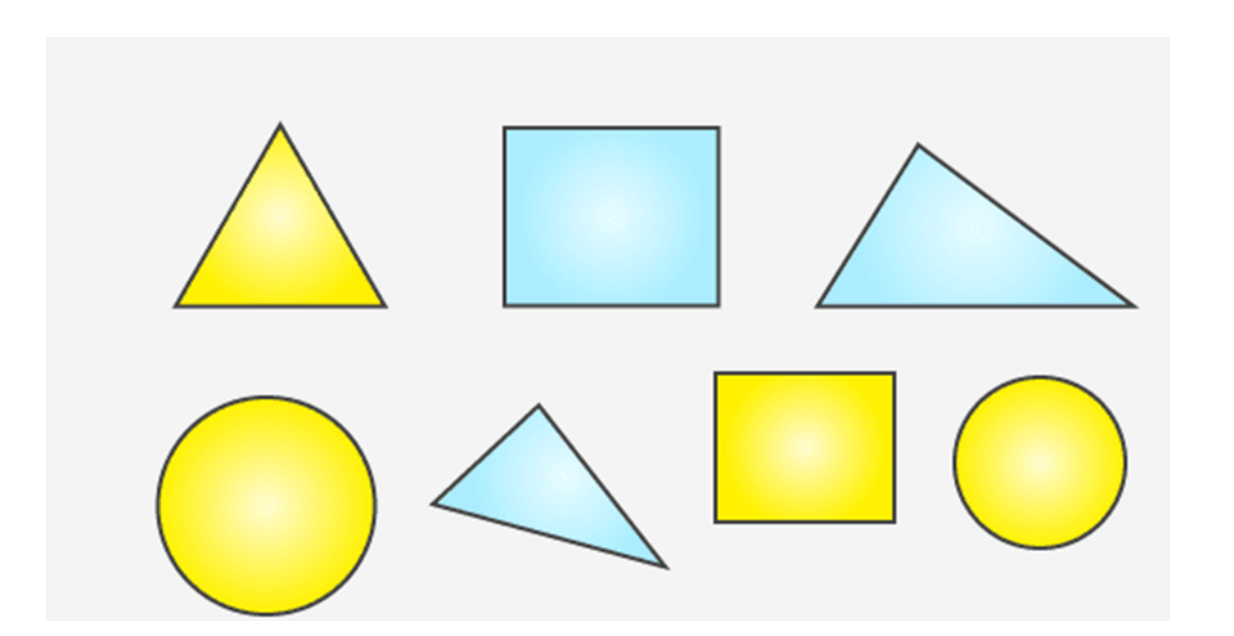See the figure and find the ratio of (a) Number of triangles to the number of circles inside the rectangle. (b) Number of squares to all the figures inside the rectangle. (c) Number of circles to all the figures inside the rectangle. Solutions: Given in the figure Number of triangles = 3 Number of circles = 2 Number of squares = 2 Total number of figures = 7 (a) Ratio of the number of triangles to the number of circles inside the rectangle = 3 / 2 (b) Ratio of the number of squares to all the figures inside the rectangle = 2 / 7 (c) Ratio of the number of circles to all the figures inside the rectangle = 2 / 7 4. The distance travelled by Hamid and Akhtar in an hour is 9 km and 12 km, respectively. Find the ratio of the speed of Hamid to the speed of Akhtar. Solutions: We know that the speed of a certain object is the distance travelled by that object in an hour Distance travelled by Hamid in one hour = 9 km Distance travelled by Akhtar in one hour = 12 km Speed of Hamid = 9 km/hr Speed of Akhtar = 12 km/hr The ratio of the speed of Hamid to the speed of Akhtar = 9 / 12 = 3 / 4 5. Fill in the blanks: 15 / 18 = ☐ / 6 = 10 / ☐ = ☐ / 30 [Are these equivalent ratios?] Solutions: 15 / 18 = (5 × 3) / (6 × 3) = 5 / 6 5 / 6 = (5 × 2) / (6 × 2) = 10 / 12 5 / 6 = (5 × 5) / (6 × 5) = 25 / 30 Hence, 5, 12 and 25 are the numbers which come in the blanks, respectively. Yes, all are equivalent ratios. 6. Find the ratio of the following: (a) 81 to 108 (b) 98 to 63 (c) 33 km to 121 km (d) 30 minutes to 45 minutes Solutions: (a) 81 / 108 = (3 × 3 × 3 × 3) / (2 × 2 × 3 × 3 × 3 ) = 3 / 4 (b) 98 / 63 = (14 × 7) / (9 × 7) = 14 / 9 (c) 33 / 121 = (3 × 11) / (11 × 11) = 3 / 11 (d) 30 / 45 = (2 × 3 × 5) / (3 × 3 × 5) = 2 / 3

CBSE Board Exam Centre List 2024

7. Find the ratio of the following: (a) 30 minutes to 1.5 hours (b) 40 cm to 1.5 m (c) 55 paise to ₹ 1 (d) 500 ml to 2 litres Solutions: (a) 30 minutes to 1.5 hours 30 min = 30 / 60 = 0.5 hours Required ratio = (0.5 × 1 ) / (0.5 × 3) = 1 / 3 (b) 40 cm to 1.5 m 1.5 m = 150 cm Required ratio = 40 / 150 = 4 / 15 (c) 55 paise to ₹ 1 ₹ 1 = 100 paise Required ratio = 55 / 100 = (11 × 5) / (20 × 5) = 11 / 20 (d) 500 ml to 2 litres 1 litre = 1000 ml 2 litre = 2000 ml Required ratio = 500 / 2000 = 5 / 20 = 5 / (5 × 4) = 1 / 4 8. In a year, Seema earns ₹ 1,50,000 and saves ₹ 50,000. Find the ratio of (a) Money that Seema earns to the money she saves (b) Money that she saves to the money she spends. Solutions: Money earned by Seema = ₹ 150000 Money saved by her = ₹ 50000 Money spent by her = ₹ 150000 – ₹ 50000 = ₹ 100000 (a) Ratio of money earned to money saved = 150000 / 50000 = 15 / 5 = 3 / 1 (b) Ratio of money saved to money spent = 50000 / 100000 = 5 / 10 = 1 / 2 9. There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students. Solutions: Given Number of teachers in the school = 102 Number of students in the school = 3300 The ratio of the number of teachers to the number of students = 102 / 3300 = (2 × 3 × 17) / (2 × 3 × 550) = 17 / 550 10. In a college, out of 4320 students, 2300 are girls. Find the ratio of (a) Number of girls to the total number of students. (b) Number of boys to the number of girls. (c) Number of boys to the total number of students. Solutions: Given Total number of students = 4320 Number of girls = 2300 Number of boys = 4320 – 2300 = 2020 (a) Ratio of the number of girls to the total number of students = 2300 / 4320 = (2 × 2 × 5 × 115) / (2 × 2 × 5 × 216) = 115 / 216 (b) Ratio of the number of boys to the number of girls = 2020 / 2300 = (2 × 2 × 5 × 101) / (2 × 2 × 5 × 115) = 101 / 115 (c) Ratio of the number of boys to the total number of students = 2020 / 4320 = (2 × 2 × 5 × 101) / (2 × 2 × 5 × 216) = 101 / 216
CBSE Syllabus Class 6
CBSE Class 6 Science Syllabus CBSE Class 6 Maths Syllabus
CBSE Class 6 Social Science Syllabus CBSE Class 6 English Syllabus
11. Out of 1800 students in a school, 750 opted for basketball, 800 opted for cricket, and the remaining opted for table tennis. If a student can opt for only one game, find the ratio of (a) The number of students who opted for basketball to the number of students who opted for table tennis. (b) The number of students who opted for cricket to the number of students opting for basketball. (c) The number of students who opted for basketball to the total number of students. Solutions: Given, Number of students in the school = 1800 The number of students who opted for basketball = 750 The number of students who opted for cricket = 800 The number of students who opted for table tennis = 1800 – (750 + 800) = 1800 – 1550 = 250

( a) Ratio of the number of students who opted for basketball to the number of students who opted for table tennis = 750 / 250 = 3 / 1

(b) Ratio of the number of students who opted for cricket to the number of students who opted for basketball = 800 / 750 = 16 / 15 (c) Ratio of the number of students who opted for basketball to the total number of students = 750 / 1800 = 25 / 60 = 5 / 12 12. The cost of a dozen pens is ₹ 180, and the cost of 8 ball pens is ₹ 56. Find the ratio of a pen's cost to a ball pen's cost. Solutions: Cost of a dozen pens = ₹ 180 Cost of 1 pen = 180 / 12 = ₹ 15 Cost of 8 ball pens = ₹ 56 Cost of 1 ball pen = 56 / 8 = ₹ 7 Hence, the required ratio is 15 / 7. 13. Consider the statement: The ratio of breadth and length of a hall is 2:5. Complete the following table that shows some possible breadths and lengths of the hall.
The breadth of the hall (in metres) 10 40
Length of the hall (in metres) 25 50
Solutions: (i) Length = 50 m Breadth / 50 = 2 / 5 By cross multiplication 5× breadth = 50 × 2 Breadth = (50 × 2) / 5 = 100 / 5 = 20 m (ii) Breadth = 40 m 40 / Length = 2 / 5 By cross multiplication 2 × Length = 40 × 5 Length = (40 × 5) / 2 Length = 200 / 2 Length = 100 m 14. Divide 20 pens between Sheela and Sangeeta in a ratio of 3:2. Solutions: Terms of 3:2 = 3 and 2 The sum of these terms = 3 + 2 = 5 Now, Sheela will get 3 / 5 of the total pens, and Sangeeta will get 2 / 5 of the total pens Number of pens with Sheela = 3 / 5 × 20 = 3 × 4 = 12 Number of pens with Sangeeta = 2 / 5 × 20 = 2 × 4 = 8 15. The mother wants to divide ₹ 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If the age of Shreya is 15 years and the age of Bhoomika is 12 years, find how much Shreya and Bhoomika will get. Solutions: Ratio of ages = 15 / 12 = 5 / 4 Hence, the mother wants to divide ₹ 36 in the ratio of 5:4 Terms of 5:4 are 5 and 4 The sum of these terms = 5 + 4 = 9 Here, Shreya will get 5 / 9 of the total money, and Sangeeta will get 4 / 9 of the total money The amount Shreya get = 5 / 9 × 36 = 20 The amount Sangeeta get = 4 / 9 × 36 = 16 Therefore, Shreya will get ₹ 20, and Sangeeta will get ₹ 16. 16. The present age of the father is 42 years, and that of his son is 14 years. Find the ratio of (a) Present age of the father to the present age of the son (b) Age of the father to the age of the son, when the son was 12 years old (c) Age of father after 10 years to the age of son after 10 years (d) Age of father to the age of son when father was 30 years old Solutions: (a) Present age of father = 42 years Present age of son = 14 years Required ratio 42 / 14 = 3 / 1 (b) 2 years ago, the son was 12 years old. So, 2 years ago, the age of the father was = 42 – 2 = 40 years Required ratio = 40 / 12 = (4 × 10) / (4 × 3) = 10 / 3 (c) After ten years, the age of the father = 42 + 10 = 52 years After 10 years, the age of the son = 14 + 10 = 24 years Required ratio = 52 / 24 = (4 × 13) / (4 × 6) = 13 / 6 (d) 12 years ago, the age of the father was 30 At that time, the age of the son = 14 – 12 = 2 years Required ratio = 30 / 2 = (2 × 15) / 2 = 15 / 1
Related Links
NCERT Solutions for Class 6 Maths Chapter 1 NCERT Solutions for Class 6 Maths Chapter 11
NCERT Solutions for Class 6 Maths Chapter 3 NCERT Solutions for Class 6 Maths Chapter 13
NCERT Solutions for Class 6 Maths Chapter 4 NCERT Solutions for Class 6 Maths Chapter 14
NCERT Solutions for Class 6 Maths Chapter 5
NCERT Solutions for Class 6 Maths Chapter 2
NCERT Solutions For Class 6 maths Chapter 7
NCERT Solutions for Class 6 Maths Chapter 6
NCERT Solutions for Class 6 Maths Chapter 8
NCERT Solutions for Class 6 Maths Chapter 9
NCERT Solutions for Class 6 Maths Chapter 10

Exercise 12.2 Page No. 255

1. Determine if the following are in proportion.

(a) 15, 45, 40, 120 (b) 33, 121, 9, 96 (c) 24, 28, 36, 48 (d) 32, 48, 70, 210 (e) 4, 6, 8, 12 (f) 33, 44, 75, 100 Solutions: (a) 15, 45, 40, 120 15 / 45 = 1 / 3 40 / 120 = 1 / 3 Hence, 15:45 = 40:120 ∴ They are in proportion. (b) 33, 121, 9, 96 33 / 121 = 3 / 11 9 / 96 = 3 / 32 Hence 33:121 ≠ 9: 96 ∴ They are not in proportion. (c) 24, 28, 36, 48 24 / 28 = 6 / 7 36 / 48 = 3 / 4 Hence, 24:28 ≠ 36:48 ∴ They are not in proportion. (d) 32, 48, 70, 210 32 / 48 = 2 / 3 70 / 210 = 1 / 3 Hence, 32:48 ≠ 70:210 ∴ They are not in proportion. (e) 4, 6, 8, 12 4 / 6 = 2 / 3 8 / 12 = 2 / 3 Hence 4: 6 = 8: 12 ∴ These are in a proportion (f) 33, 44, 75, 100 33/ 44 = 3/ 4 75 / 100 = 3 / 4 Hence, 33:44 = 75:100 ∴ These are in proportion. 2. Write True (T) or False ( F ) against each of the following statements : (a) 16:24 :: 20:30 (b) 21:6 :: 35:10 (c) 12:18 :: 28:12 (d) 8:9 :: 24:27 (e) 5.2:3.9 :: 3:4 (f) 0.9:0.36 :: 10:4 Solutions: (a) 16:24 :: 20:30 16 / 24 = 2 / 3 20 / 30 = 2 / 3 Hence, 16:24 = 20:30 Therefore, True. (b) 21:6 :: 35:10 21 / 6 = 7 / 2 35 / 10 = 7 / 2 Hence, 21:6 = 35:10 Therefore, True. (c) 12:18 :: 28:12 12 / 18 = 2 / 3 28 / 12 = 7 / 3 Hence, 12:18 ≠ 28:12 Therefore, False, (d) 8:9:: 24:27 We know that = 24 / 27 = (3 × 8) / (3 × 9) = 8 / 9 Hence, 8:9 = 24:27 Therefore, True. (e) 5.2:3.9 :: 3: 4 As 5.2 / 3.9 = 4 / 3 Hence, 5.2: 3.9 ≠ 3: 4 Therefore, False, (f) 0.9:0.36 :: 10:4 0.9 / 0.36 = 90 / 36 = 10 / 4 Hence, 0.9: 0.36 = 10: 4 Therefore, True, 3. Are the following statements true? (a) 40 persons: 200 persons = ₹ 15 : ₹ 75 (b) 7.5 litres: 15 litres = 5 kg : 10 kg (c) 99 kg: 45 kg = ₹ 44 : ₹ 20 (d) 32 m: 64 m = 6 sec : 12 sec (e) 45 km : 60 km = 12 hours : 15 hours Solutions: (a) 40 persons : 200 persons = ₹ 15 : ₹ 75 40 / 200 = 1 / 5 15 / 75 = 1 / 5 Hence, True. (b) 7.5 litres : 15 litres = 5 kg : 10 kg 7.5 / 15 = 1 / 2 5 / 10 = 1 / 2 Hence, True. (c) 99 kg : 45 kg = ₹ 44 : ₹ 20 99 / 45 = 11 / 5 44 / 20 = 11 / 5 Hence, True. (d) 32 m : 64 m = 6 sec : 12 sec 32 / 64 = 1 / 2 6 / 12 = 1 / 2 Hence, True. (e) 45 km : 60 km = 12 hours : 15 hours 45 / 60 = 3 / 4 12 / 15 = 4 / 5 Hence, False.

Class 6 Maths Chapter 12: Topics

Ratio and Proportion mainly shows the difference between two numbers. Ratio If the total number of boys in a class is 40 and the total number of girls in a class is 50. Then the ratio between the number of boys and girls in a class is 40 / 50, which is 4:5. The number of students in a class is equal to the sum of the number of boys in a class and the number of girls in a class. The ratio between the number of students in a class and the number of girls in a class is 90 / 50 which is 9: 5 Proportion If the two sets of numbers are in the same ratio, then the numbers are said to be the proportion. For example,  40: 50 and 800: 1000 Here, 40: 50 can be written as 4: 5 and 800: 1000 can be written as 4:5 So, 40: 50 and 800: 1000 are in proportion. Compare 70:60 and 40: 80 Here, 70:60 can be written as 7:6 and 40:80 can be written as 1:2 So, 70:60 and 40:80 are not in proportion. Unitary Method In the unitary method, we need to find the answer for one product and calculate it for many. For example: The Cost of 2 litre petrol is Rs. 50. What is the cost of 10 litre petrol Here, we need to calculate the cost of 1 litre of petrol, That is 50/2 = 25. Then the cost of 10-litre petrol is 250.

Key Features of NCERT Solutions for Class 6 Maths Chapter 12

Every learner must aim to achieve high grades in exams. The Class 6 Maths NCERT solutions will assist the student in the following ways.
  • Students will grasp fundamental ideas about Ratio and Proportion at the 6th-grade level.
  • They can clarify any uncertainties regarding 6th-grade Maths Ratio and Proportion.
  • The NCERT Solutions for Class 6 Maths Chapter 12 will enable students to secure good marks in the examination.

NCERT Solutions for Class 6 Maths Chapter 12 FAQs

Do I need to make notes while referring to NCERT Solutions of Maths for Chapter 12 of Class 6?

While making notes while using NCERT Solutions for Class 6 Maths Chapter 12 is not mandatory, creating personalised notes can reinforce your understanding and serve as a handy revision tool.

What are the best ways to learn concepts in Class 6 Maths of Chapter 12?

The best ways to learn concepts in Class 6 Maths Chapter 12 include regular practice through exercises, seeking clarification on doubts, and using interactive methods like visual aids or group discussions to enhance understanding.

How can CBSE Students utilise Maths NCERT Solutions effectively for Chapter 12 of Class 6 Maths?

CBSE students can effectively utilise Math NCERT Solutions for Chapter 12 by incorporating them into a consistent study routine, practising regularly, and seeking additional help or clarification when needed.

Are NCERT Solutions of Chapter 12 in Maths of Class 6 sufficient for CBSE Exams?

Yes, NCERT Solutions of Chapter 12 in Maths for Class 6 are designed to cover the CBSE curriculum comprehensively. However, supplementing with additional practice and resources can further strengthen preparation for CBSE exams.

Explain the golden ratio covered in Chapter 12 of NCERT Solutions for Class 6 Maths.

The golden ratio, covered in Chapter 12 of NCERT Solutions for Class 6 Maths, is a special number approximately equal to 1.618. It appears in various natural phenomena and art, showcasing its significance in aesthetics and mathematics.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
07019243492
Check out these Related Articles
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Maths Ganita Prakash Chapter 5 Prime Time
Read Full Story
27 Jun 2025, 01:06 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Science Curiosity Chapter Wise PDF
Read Full Story
24 Jun 2025, 11:03 am
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Social Science Chapter 7 India’s Cultural Roots
Read Full Story
23 Jun 2025, 01:34 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Maths Ganita Prakash Chapter 4 Question Answer
Read Full Story
26 Jun 2025, 01:21 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Maths Ganita Prakash Chapter 3 Number Play
Read Full Story
25 Jun 2025, 02:05 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Social Science Chapter Wise PDF Available
Read Full Story
23 Jun 2025, 07:03 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Maths Ganita Prakash Chapter 2 Solution PDF
Read Full Story
24 Jun 2025, 01:19 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Social Science Chapter 3 Landforms and Life
Read Full Story
24 Jun 2025, 12:53 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Solutions for Class 6 Social Science Chapter 2 Question Answer PDF
Read Full Story
24 Jun 2025, 04:14 pm
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.