
NCERT Solutions for Class 6 Maths Chapter 5
NCERT Solutions for Class 6 Maths Chapter 5: NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes are accessible here, aiding students in effective learning. These materials, available in PDF format, can be downloaded for offline practice. PW provides online learning resources, including notes, question papers, and exemplar problems for various classes. Students can use these resources as worksheets to prepare for exams. NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes are presented here to assist students in their exam readiness. Practicing the solved problems in NCERT Class 6 Chapter 5 helps students understand how to solve different types of questions.NCERT Solutions for Class 6 Maths Chapter 5 Overview
In the intriguing world of mathematics, the exploration of shapes plays a crucial role. Chapter 5 of NCERT Solutions for Class 6 Maths, titled 'Understanding Elementary Shapes,' takes students on an enlightening journey into the captivating realm of geometric forms and their properties. This chapter serves as a foundation for understanding the basic principles of shapes, angles, and lines, crucial not just in mathematics but also in daily life. Our carefully crafted solutions serve as a comprehensive guide to mastering the intricacies of elementary shapes, allowing students to solve problems and explore the geometric wonders that surround us. Delve into this enriching chapter, where the study of shapes reveals a world of order, symmetry, and mathematical beauty, empowering young minds to grasp the language of geometry with confidence. NCERT Solutions for Class 6 Maths Chapter 5 provide precise and accurate answers to questions from this specific chapter. Studying alongside the textbook will enhance students' preparation and enable them to achieve higher scores in their final exams.NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes
Chapter 5 of Class 6 Mathematics explores different shapes found in the world around us. It's crucial for students to grasp various geometrical shapes, and this solution assists them in doing so. This chapter comprises ten topics, each addressing a different idea. It starts by explaining how to measure different line segments and then delves into more advanced concepts like angles and various geometrical shapes. The NCERT Solutions for Class 6 Maths Chapter 5 serve as essential study material for sixth-grade students. They provide a thorough yet easy-to-understand understanding of this important mathematical concept. These solutions aid students in quickly grasping the topics and enhancing their exam preparations. Exercise 5.1 Page No: 88 1. What is the disadvantage in comparing line segments by mere observation? Solutions: By mere observation we can’t compare the line segments with slight difference in their length. We can’t say which line segment is of greater length. Hence, the chances of errors due to improper viewing are higher. 2. Why is it better to use a divider than a ruler, while measuring the length of a line segment? Solutions: While using a ruler, chances of error occur due to thickness of the ruler and angular viewing. Hence, using divider accurate measurement is possible. 3. Draw any line segment, say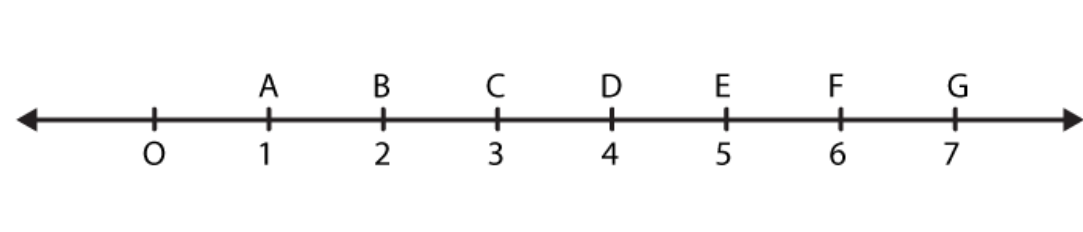 Solutions:
Since, it is clear from the figure that AD = DG = 3 units. Hence, D is the midpoint of
Solutions:
Since, it is clear from the figure that AD = DG = 3 units. Hence, D is the midpoint of
6. If B is the mid point of
![]() and C is the mid point of
and C is the mid point of
![]() , where A, B, C, D lie on a straight line, say why AB = CD?
, where A, B, C, D lie on a straight line, say why AB = CD?
 Given
B is the midpoint of AC. Hence, AB = BC (1)
C is the midpoint of BD. Hence, BC = CD (2)
From (1) and (2)
AB = CD is verified
7. Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Solutions:
Given
B is the midpoint of AC. Hence, AB = BC (1)
C is the midpoint of BD. Hence, BC = CD (2)
From (1) and (2)
AB = CD is verified
7. Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Solutions:
Case 1. In triangle ABC
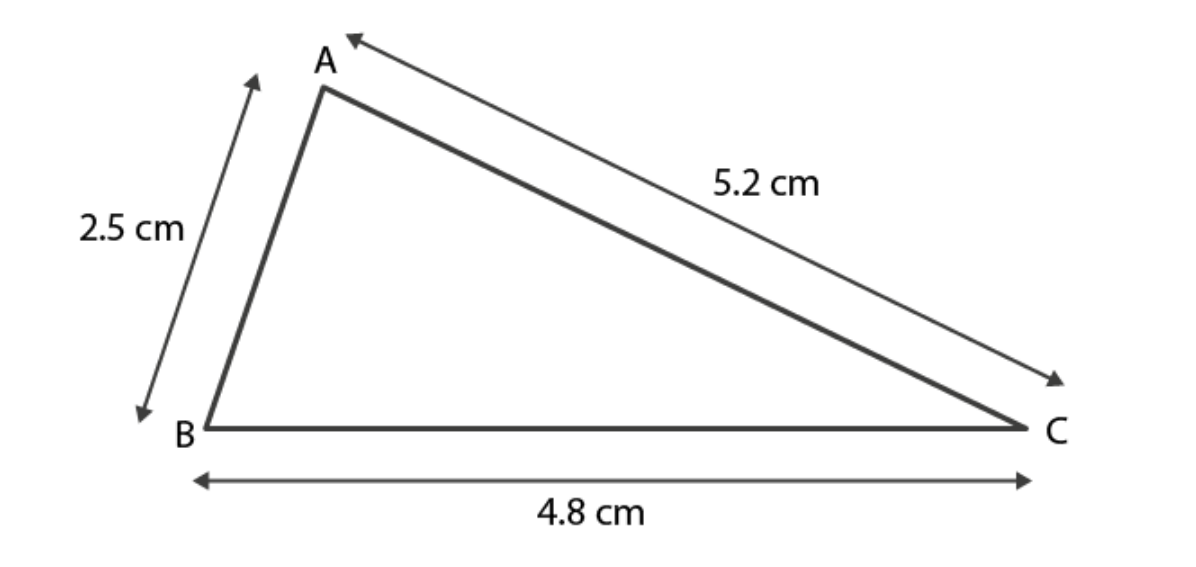 AB= 2.5 cm
BC = 4.8 cm and
AC = 5.2 cm
AB + BC = 2.5 cm + 4.8 cm
= 7.3 cm
As 7.3 > 5.2
∴ AB + BC > AC
Hence, the sum of any two sides of a triangle is greater than the third side.
AB= 2.5 cm
BC = 4.8 cm and
AC = 5.2 cm
AB + BC = 2.5 cm + 4.8 cm
= 7.3 cm
As 7.3 > 5.2
∴ AB + BC > AC
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 2. In triangle PQR
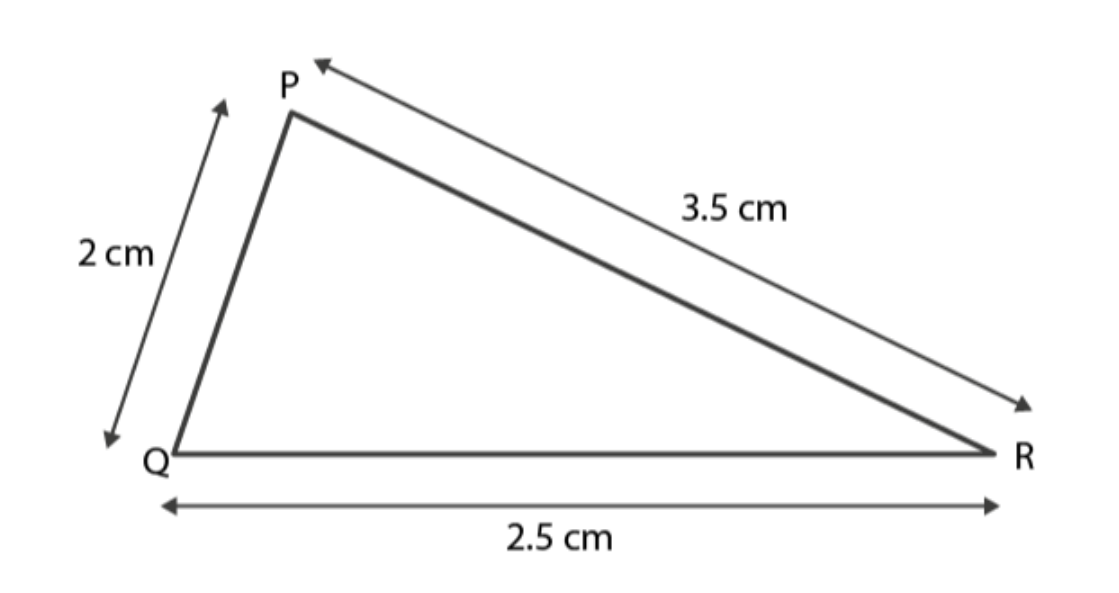 PQ = 2 cm
QR = 2.5 cm
PR = 3.5 cm
PQ + QR = 2 cm + 2.5 cm
= 4.5 cm
As 4.5 > 3.5
∴ PQ + QR > PR
Hence, the sum of any two sides of a triangle is greater than the third side.
PQ = 2 cm
QR = 2.5 cm
PR = 3.5 cm
PQ + QR = 2 cm + 2.5 cm
= 4.5 cm
As 4.5 > 3.5
∴ PQ + QR > PR
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 3. In triangle XYZ
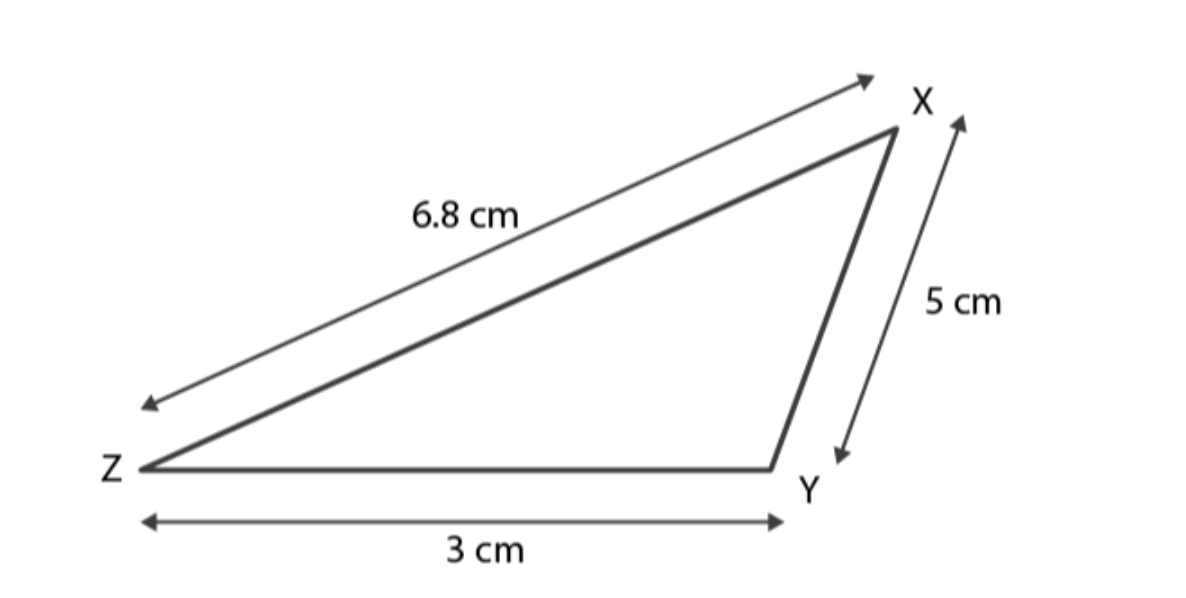 XY = 5 cm
YZ = 3 cm
ZX = 6.8 cm
XY + YZ = 5 cm + 3 cm
= 8 cm
As 8 > 6.8
∴ XY + YZ > ZX
Hence, the sum of any two sides of a triangle is greater than the third side.
XY = 5 cm
YZ = 3 cm
ZX = 6.8 cm
XY + YZ = 5 cm + 3 cm
= 8 cm
As 8 > 6.8
∴ XY + YZ > ZX
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 4. In triangle MNS
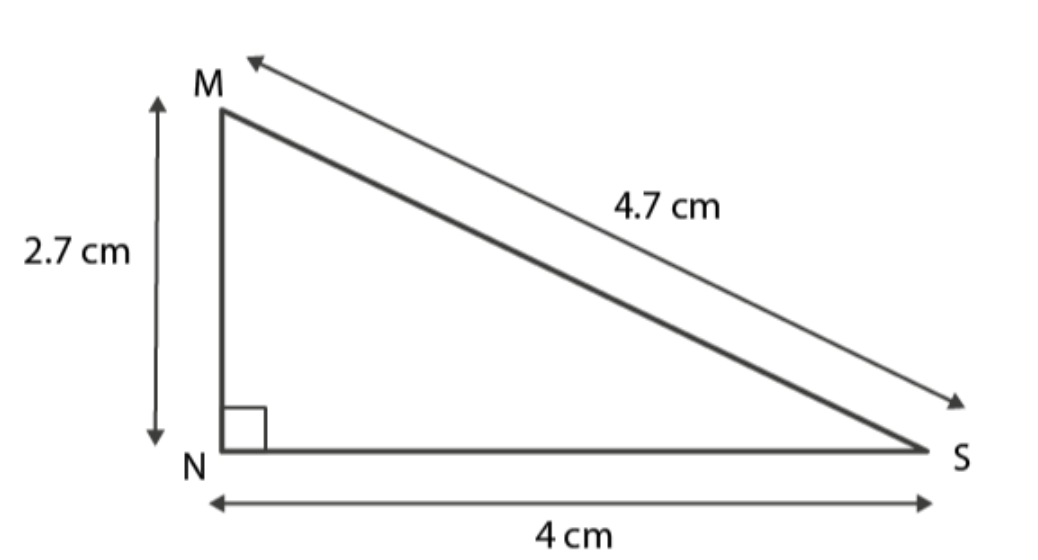 MN = 2.7 cm
NS = 4 cm
MS = 4.7 cm
MN + NS = 2.7 cm + 4 cm
6.7 cm
As 6.7 > 4.7
∴ MN + NS > MS
Hence, the sum of any two sides of a triangle is greater than the third side.
MN = 2.7 cm
NS = 4 cm
MS = 4.7 cm
MN + NS = 2.7 cm + 4 cm
6.7 cm
As 6.7 > 4.7
∴ MN + NS > MS
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 5. In triangle KLM
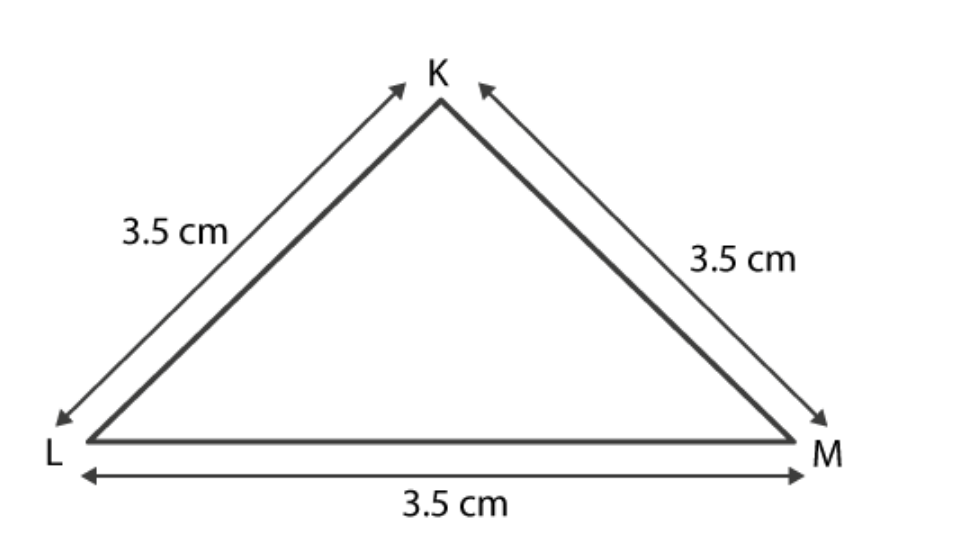 KL = 3.5 cm
LM = 3.5 cm
KM = 3.5 cm
KL + LM = 3.5 cm + 3.5 cm
= 7 cm
As 7 cm > 3.5 cm
∴ KL + LM > KM
Hence, the sum of any two sides of a triangle is greater than the third side.
Therefore, we conclude that the sum of any two sides of a triangle is always greater than the third side.
Exercise 5.2 Page No: 91
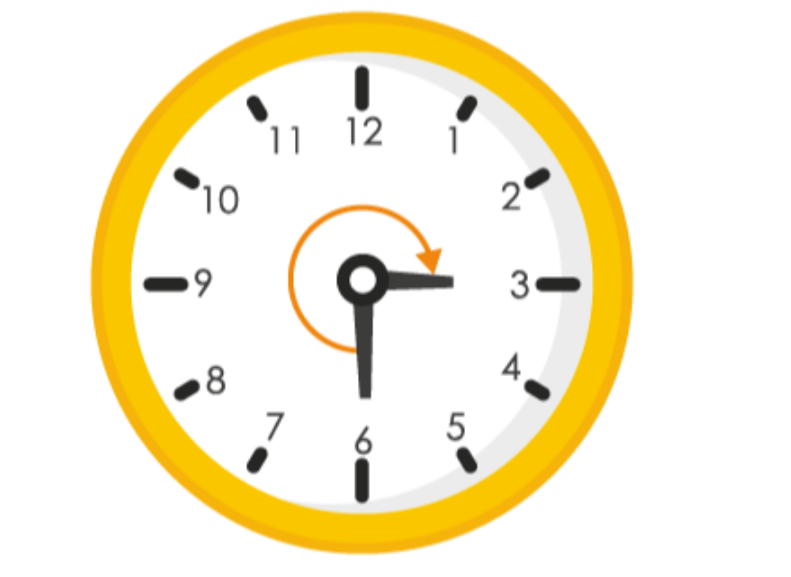
1. What fraction of a clockwise revolution does the hour hand of a clock turn through, when it goes from
(a) 3 to 9
(b) 4 to 7
(c) 7 to 10
(d) 12 to 9
(e) 1 to 10
(f) 6 to 3
Solutions:
We know that in one complete clockwise revolution, hour hand will rotate by 360
0
(a)
When hour hand goes from 3 to 9 clockwise, it will rotate by 2 right angles or 180
0
∴ Fraction = 180
0
/ 360
0
= 1 / 2
KL = 3.5 cm
LM = 3.5 cm
KM = 3.5 cm
KL + LM = 3.5 cm + 3.5 cm
= 7 cm
As 7 cm > 3.5 cm
∴ KL + LM > KM
Hence, the sum of any two sides of a triangle is greater than the third side.
Therefore, we conclude that the sum of any two sides of a triangle is always greater than the third side.
Exercise 5.2 Page No: 91
1. What fraction of a clockwise revolution does the hour hand of a clock turn through, when it goes from
(a) 3 to 9
(b) 4 to 7
(c) 7 to 10
(d) 12 to 9
(e) 1 to 10
(f) 6 to 3
Solutions:
We know that in one complete clockwise revolution, hour hand will rotate by 360
0
(a)
When hour hand goes from 3 to 9 clockwise, it will rotate by 2 right angles or 180
0
∴ Fraction = 180
0
/ 360
0
= 1 / 2
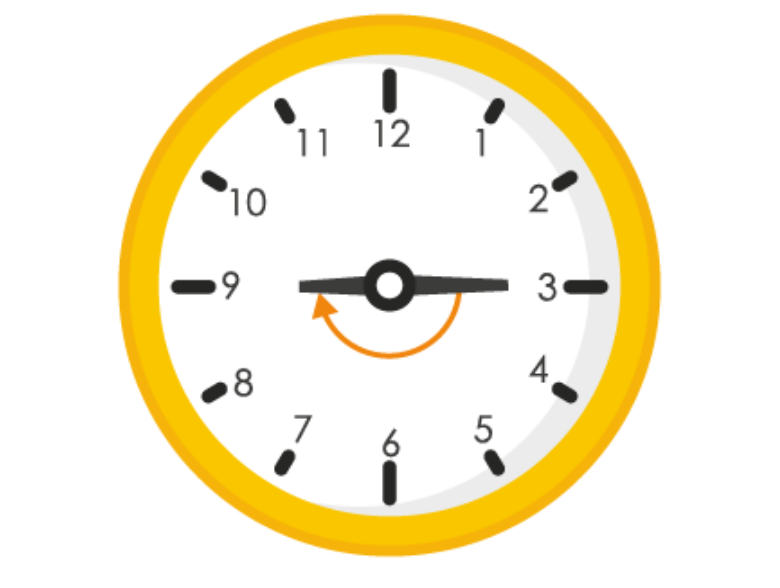 (b)
When hour hand goes from 4 to 7 clockwise, it will rotate by 1 right angle or 90
0
∴ Fraction = 90
0
/ 360
0
= 1 / 4
(b)
When hour hand goes from 4 to 7 clockwise, it will rotate by 1 right angle or 90
0
∴ Fraction = 90
0
/ 360
0
= 1 / 4
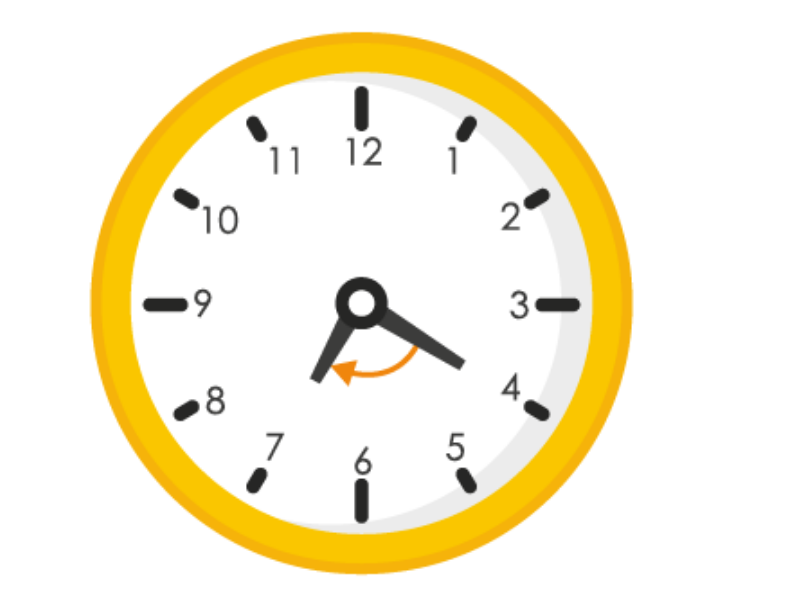 (c)
When hour hand goes from 7 to 10 clockwise, it will rotate by 1 right angle or 90
0
∴ Fraction = 90
0
/ 360
0
= 1 / 4
(c)
When hour hand goes from 7 to 10 clockwise, it will rotate by 1 right angle or 90
0
∴ Fraction = 90
0
/ 360
0
= 1 / 4
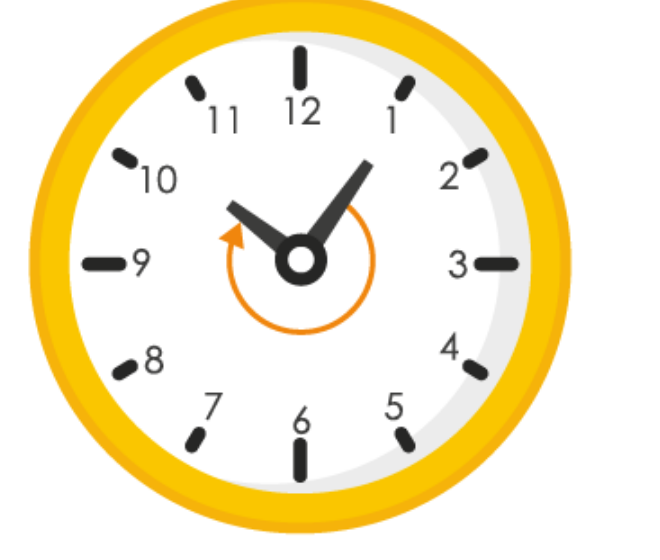
 (d)
When hour hand goes from 12 to 9 clockwise, it will rotate by 3 right angles or 270
0
∴ Fraction = 270
0
/ 360
0
= 3 / 4
(d)
When hour hand goes from 12 to 9 clockwise, it will rotate by 3 right angles or 270
0
∴ Fraction = 270
0
/ 360
0
= 3 / 4
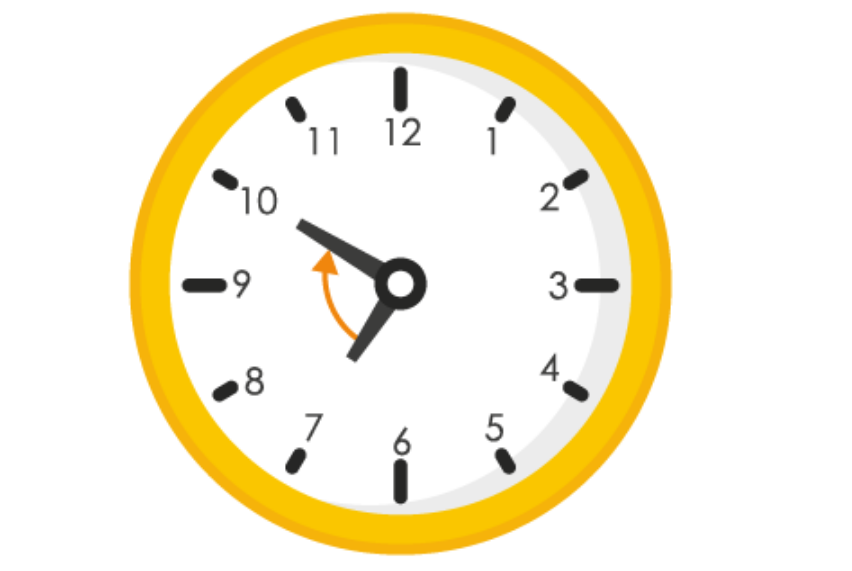
 (e)
When hour hand of a clock goes from 1 to 10 clockwise, it will rotate by 3 right angles or 270
0
∴ Fraction = 270
0
/ 360
0
= 3 / 4
(e)
When hour hand of a clock goes from 1 to 10 clockwise, it will rotate by 3 right angles or 270
0
∴ Fraction = 270
0
/ 360
0
= 3 / 4
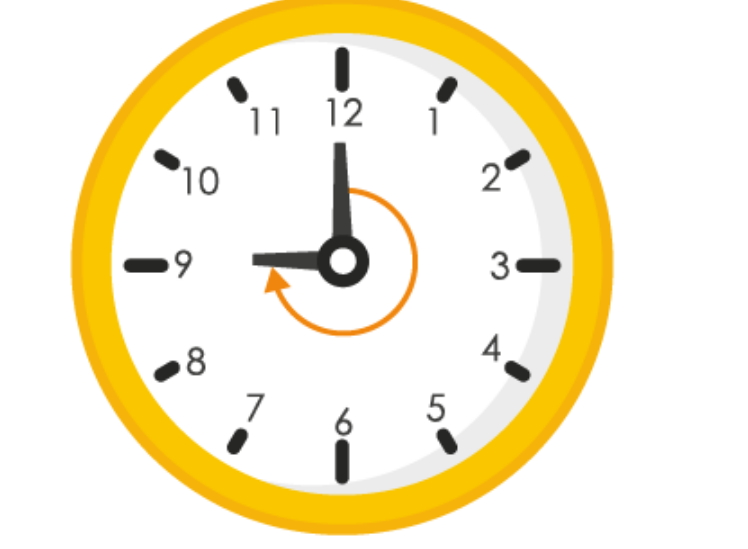
 (f)
When hour hand goes from 6 to 3 clockwise, it will rotate by 3 right angles or 270
0
∴ Fraction = 270
0
/ 360
0
= 3 / 4
(f)
When hour hand goes from 6 to 3 clockwise, it will rotate by 3 right angles or 270
0
∴ Fraction = 270
0
/ 360
0
= 3 / 4
 (a) starts at 5 and makes 3 / 4 of a revolution, clockwise?
Solutions:
We know that one complete clockwise revolution, hour hand will rotate by 360
0
(a) When hour hand of a clock starts at 12 and makes 1 / 2 revolution clockwise, it will rotate by 180
0
.
Hence, the hour hand of a clock will stop at 6.
(a) starts at 5 and makes 3 / 4 of a revolution, clockwise?
Solutions:
We know that one complete clockwise revolution, hour hand will rotate by 360
0
(a) When hour hand of a clock starts at 12 and makes 1 / 2 revolution clockwise, it will rotate by 180
0
.
Hence, the hour hand of a clock will stop at 6.
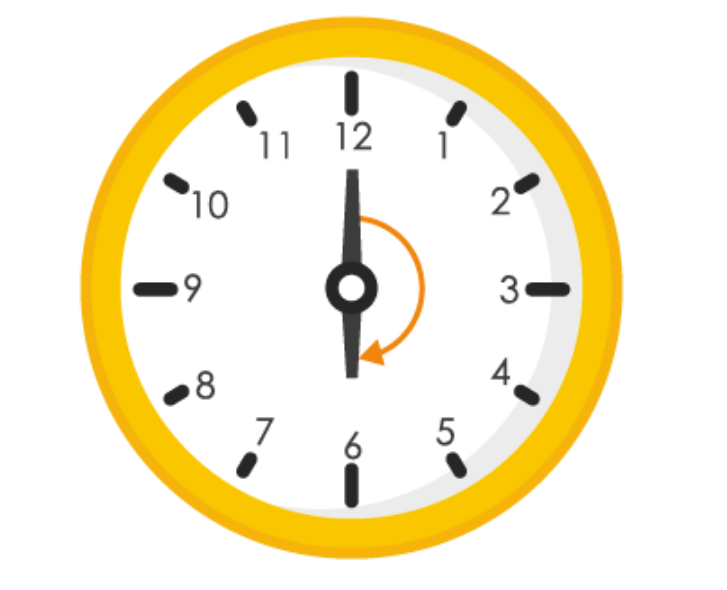 (b)
When hour hand of a clock starts at 2 and makes 1 / 2 revolution clockwise, it will rotate by 180
0
Hence, the hour hand of a clock will stop at 8.
(b)
When hour hand of a clock starts at 2 and makes 1 / 2 revolution clockwise, it will rotate by 180
0
Hence, the hour hand of a clock will stop at 8.
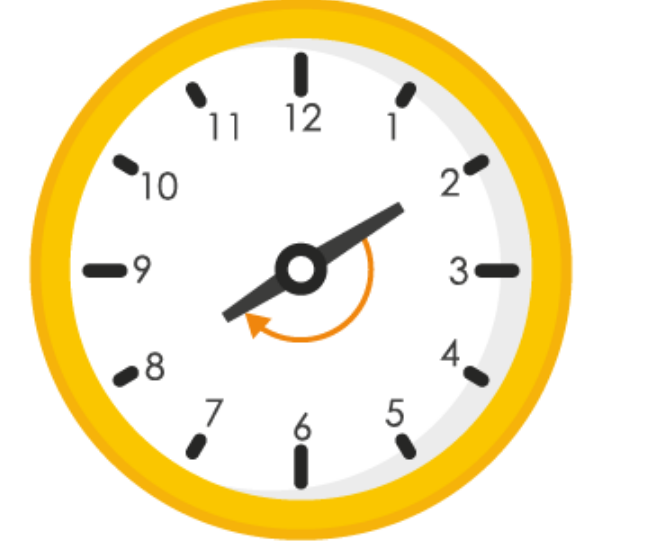 (c)
When hour hand of a clock starts at 5 and makes 1 / 4 revolution clockwise, it will rotate by 90
0
Hence, hour hand of a clock will stop at 8.
(c)
When hour hand of a clock starts at 5 and makes 1 / 4 revolution clockwise, it will rotate by 90
0
Hence, hour hand of a clock will stop at 8.
 (d)
When hour hand of a clock starts at 5 and makes 3 / 4 revolution clockwise, it will rotate by 270
0
Hence, hour hand of a clock will stop at 2
(d)
When hour hand of a clock starts at 5 and makes 3 / 4 revolution clockwise, it will rotate by 270
0
Hence, hour hand of a clock will stop at 2
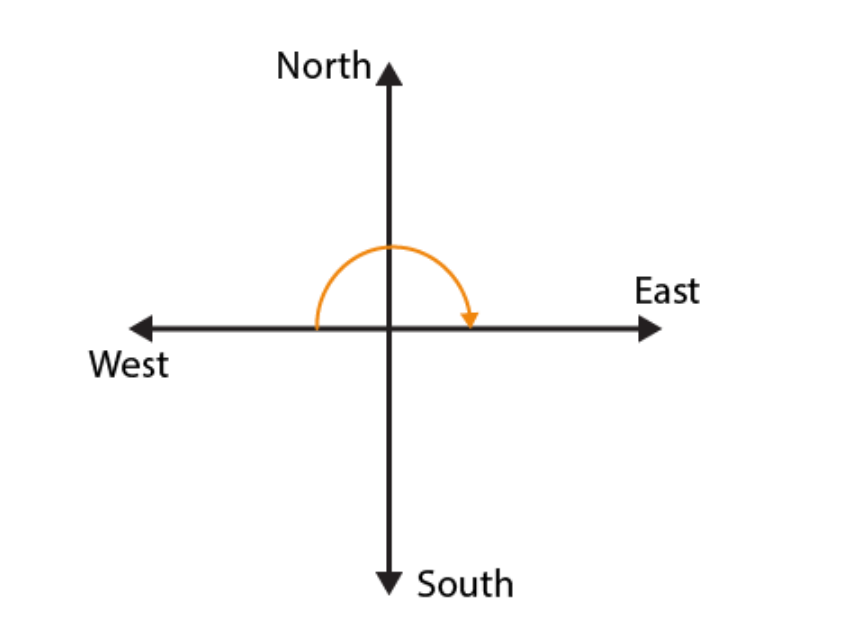
 3. Which direction will you face if you start facing
(a) east and make 1 / 2 of a revolution clockwise?
(b) east and make 1 ½ of a revolution clockwise?
(c) west and make 3 / 4 of a revolution anti – clockwise?
(d) south and make one full revolution?
(should we specify clockwise or anti – clockwise for this last question? Why not?)
Solutions:
Revolving one complete round in clockwise or in anti – clockwise direction we will revolve by 360
0
and two adjacent directions are at 90
0
or 1 / 4 of a complete revolution away from each other.
(a)
If we start facing towards East and make 1 / 2 of a revolution clockwise, we will face towards West direction.
3. Which direction will you face if you start facing
(a) east and make 1 / 2 of a revolution clockwise?
(b) east and make 1 ½ of a revolution clockwise?
(c) west and make 3 / 4 of a revolution anti – clockwise?
(d) south and make one full revolution?
(should we specify clockwise or anti – clockwise for this last question? Why not?)
Solutions:
Revolving one complete round in clockwise or in anti – clockwise direction we will revolve by 360
0
and two adjacent directions are at 90
0
or 1 / 4 of a complete revolution away from each other.
(a)
If we start facing towards East and make 1 / 2 of a revolution clockwise, we will face towards West direction.
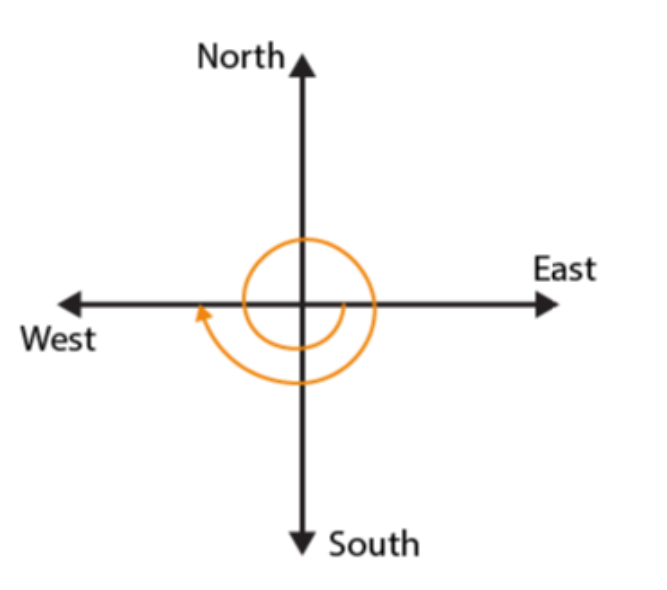
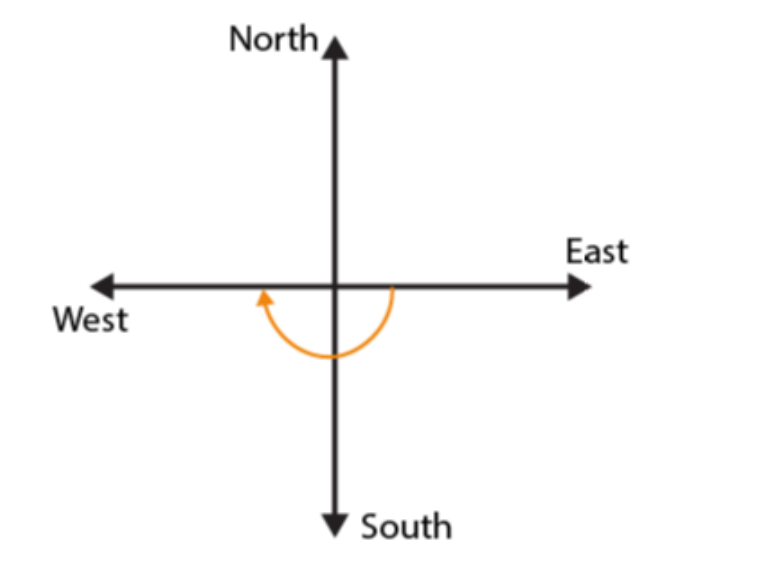 (b)
If we start facing towards East and make 1 ½ of a revolution clockwise, we will face towards West direction
(b)
If we start facing towards East and make 1 ½ of a revolution clockwise, we will face towards West direction
CBSE Board Exam Centre List 2024
(c) If we start facing towards West and make 3 / 4 of a revolution anti – clockwise, we will face towards North direction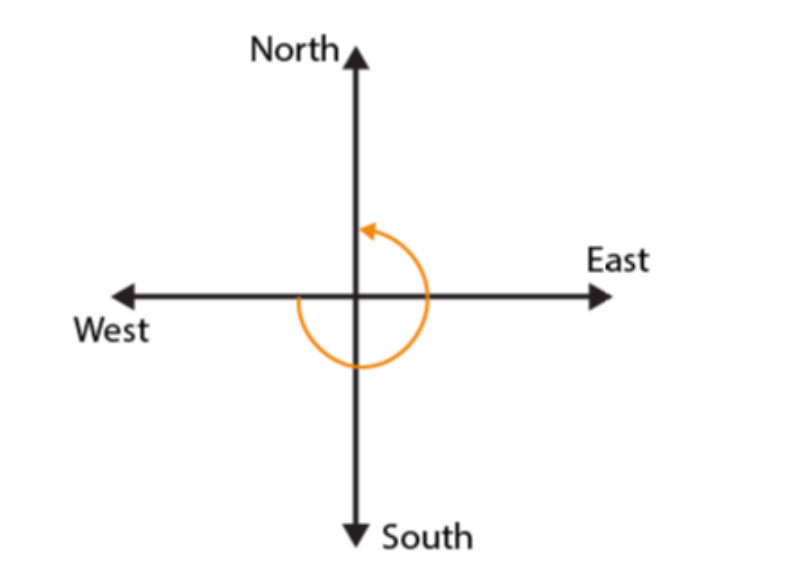 (d)
If we start facing South and make one full revolution, again we will face the South direction.
(d)
If we start facing South and make one full revolution, again we will face the South direction.
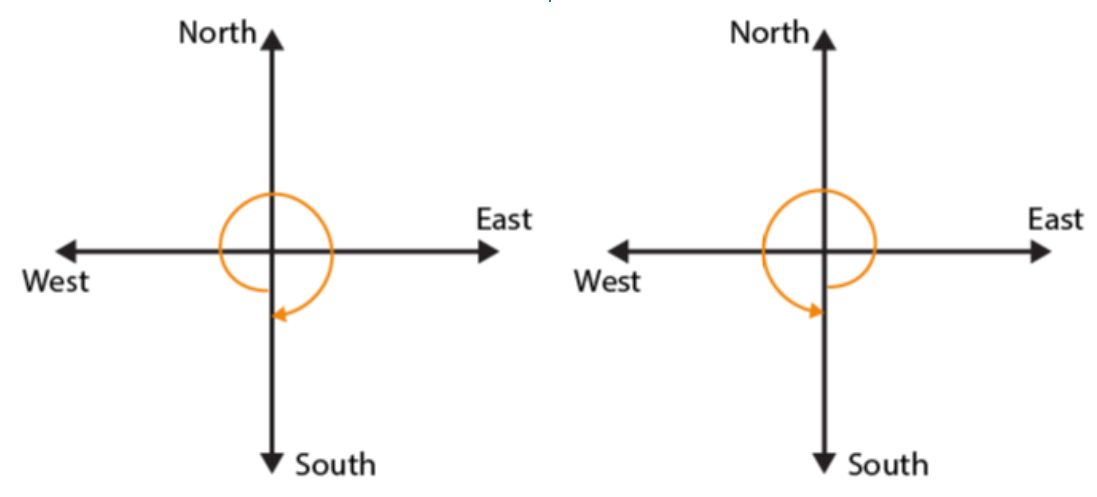 In case of revolving 1 complete revolution, either clockwise or anti-clockwise we will be back at the original position.
4. What part of a revolution have you turned through if you stand facing
(a) east and turn clockwise to face north?
(b) south and turn clockwise to face east
(c) west and turn clockwise to face east?
Solutions:
By revolving one complete revolution either in clockwise or in anti-clockwise direction, we will revolve by 360
0
and two adjacent directions are at 90
0
or 1 / 4 of a complete revolution away from each other
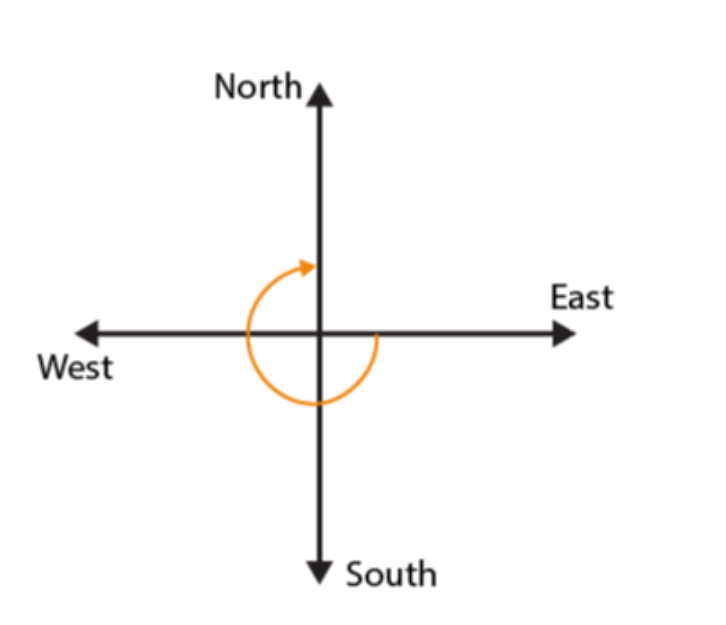
(a)
If we start facing towards East and turn clockwise to face North, we have to make 3 / 4 of a revolution
In case of revolving 1 complete revolution, either clockwise or anti-clockwise we will be back at the original position.
4. What part of a revolution have you turned through if you stand facing
(a) east and turn clockwise to face north?
(b) south and turn clockwise to face east
(c) west and turn clockwise to face east?
Solutions:
By revolving one complete revolution either in clockwise or in anti-clockwise direction, we will revolve by 360
0
and two adjacent directions are at 90
0
or 1 / 4 of a complete revolution away from each other
(a)
If we start facing towards East and turn clockwise to face North, we have to make 3 / 4 of a revolution
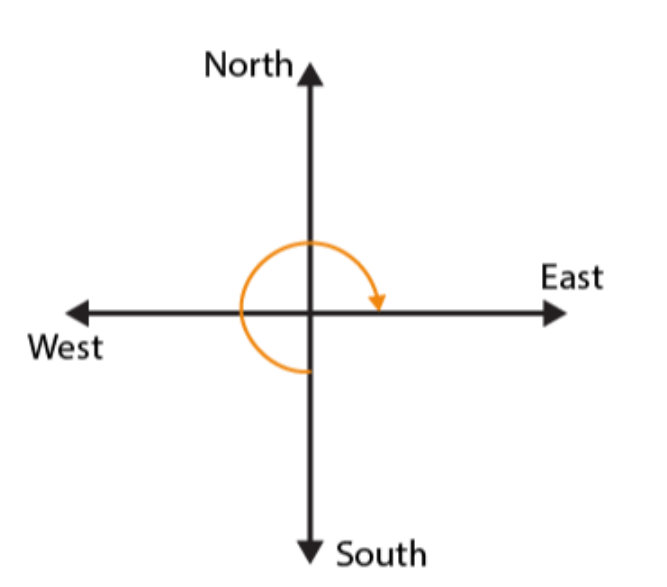
 (b)
If we start facing towards South and turn clockwise to face East, we have to make 3 / 4 of a revolution
(b)
If we start facing towards South and turn clockwise to face East, we have to make 3 / 4 of a revolution
 (c)
If we start facing towards West and turn clockwise to face East, we have to make 1 / 2 of a revolution
(c)
If we start facing towards West and turn clockwise to face East, we have to make 1 / 2 of a revolution
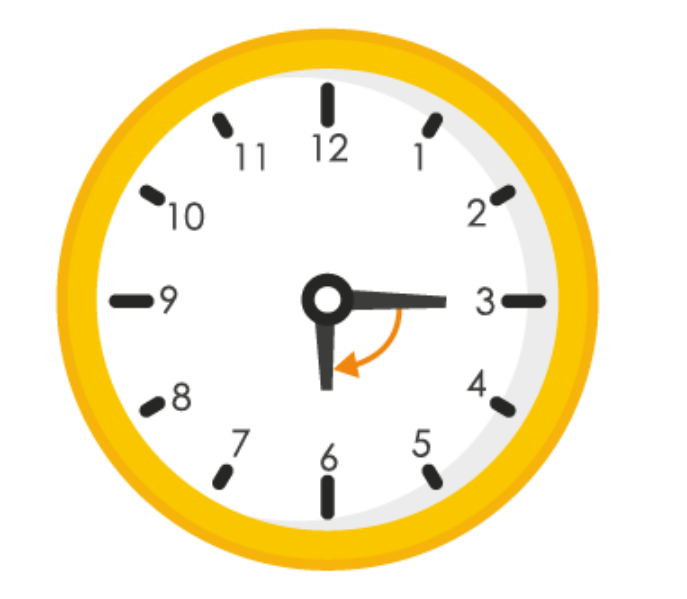
 5. Find the number of right angles turned through by the hour hand of a clock when it goes from
(a) 3 to 6
(b) 2 to 8
(c) 5 to 11
(d) 10 to 1
(e) 12 to 9
(f) 12 to 6
Solutions:
The hour hand of a clock revolves by 360
0
or it covers 4 right angles in one complete revolution
(a)
If hour hand of a clock goes from 3 to 6, it revolves by 90
0
or 1 right angle
5. Find the number of right angles turned through by the hour hand of a clock when it goes from
(a) 3 to 6
(b) 2 to 8
(c) 5 to 11
(d) 10 to 1
(e) 12 to 9
(f) 12 to 6
Solutions:
The hour hand of a clock revolves by 360
0
or it covers 4 right angles in one complete revolution
(a)
If hour hand of a clock goes from 3 to 6, it revolves by 90
0
or 1 right angle
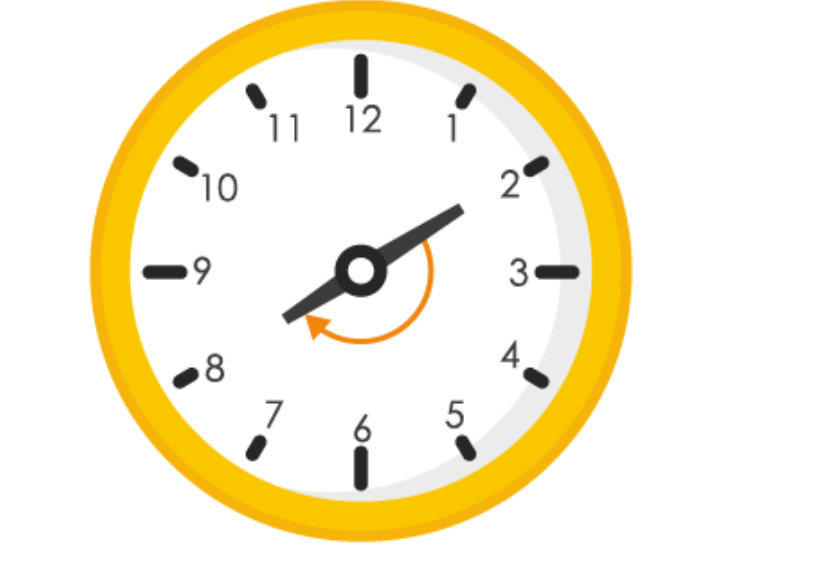
 (b)
If hour hand of a clock goes from 2 to 8, it revolves by 180
0
or 2 right angles
(b)
If hour hand of a clock goes from 2 to 8, it revolves by 180
0
or 2 right angles
 (c)
If hour hand of a clock goes from 5 to 11, it revolves by 180 degree
or 2 right angles
(c)
If hour hand of a clock goes from 5 to 11, it revolves by 180 degree
or 2 right angles
 (d)
If hour hand of a clock goes from 10 to 1, it revolves by 90 degree
or 1 right angle
(d)
If hour hand of a clock goes from 10 to 1, it revolves by 90 degree
or 1 right angle
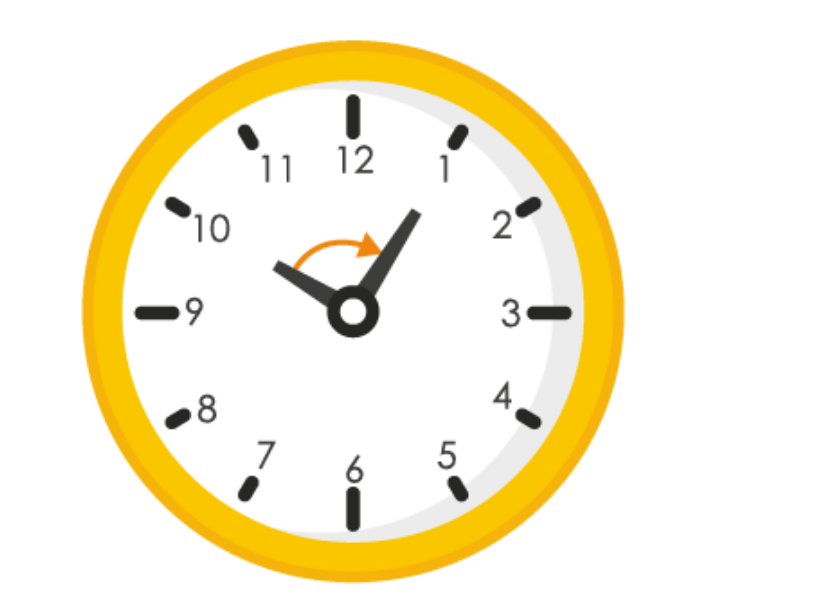 (e)
If hour hand of a clock goes from 12 to 9, it revolves by 270
0
or 3 right angles
(e)
If hour hand of a clock goes from 12 to 9, it revolves by 270
0
or 3 right angles
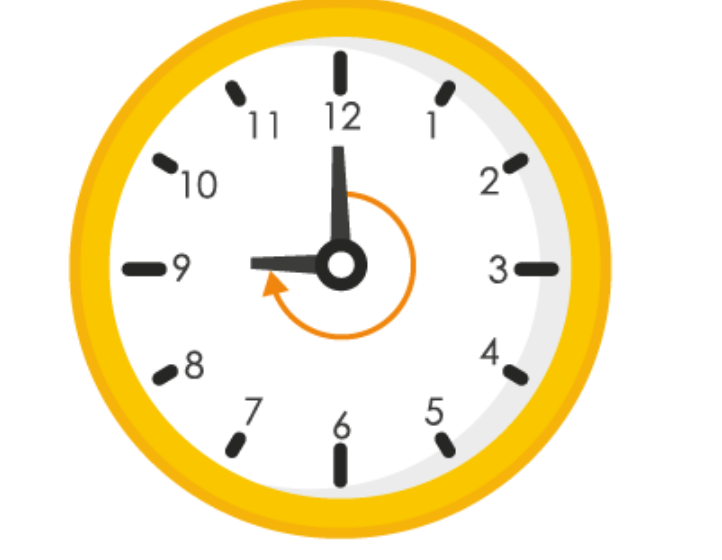 (f)
If hour hand of a clock goes from 12 to 6, it revolves by 180 degree
or 2 right angles
(f)
If hour hand of a clock goes from 12 to 6, it revolves by 180 degree
or 2 right angles
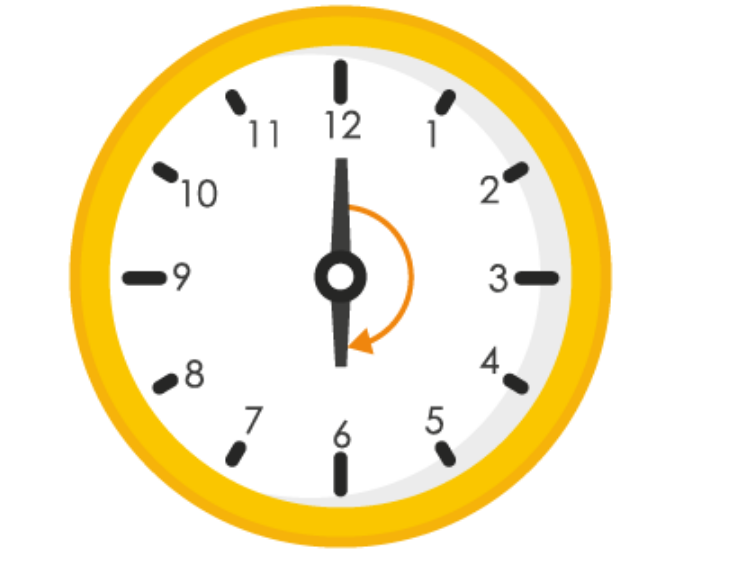 6. How many right angles do you make if you start facing
(a) south and turn clockwise to west?
(b) north and turn anti – clockwise to east?
(c) west and turn to west?
(d) south and turn to north?
Solutions:
By revolving one complete round in either clockwise or anti-clockwise direction, we will revolve by 360
0
and two adjacent directions are at 90
0
away from each other.
(a)
If we start facing towards South and turn clockwise to West, we have to make one right angle
6. How many right angles do you make if you start facing
(a) south and turn clockwise to west?
(b) north and turn anti – clockwise to east?
(c) west and turn to west?
(d) south and turn to north?
Solutions:
By revolving one complete round in either clockwise or anti-clockwise direction, we will revolve by 360
0
and two adjacent directions are at 90
0
away from each other.
(a)
If we start facing towards South and turn clockwise to West, we have to make one right angle
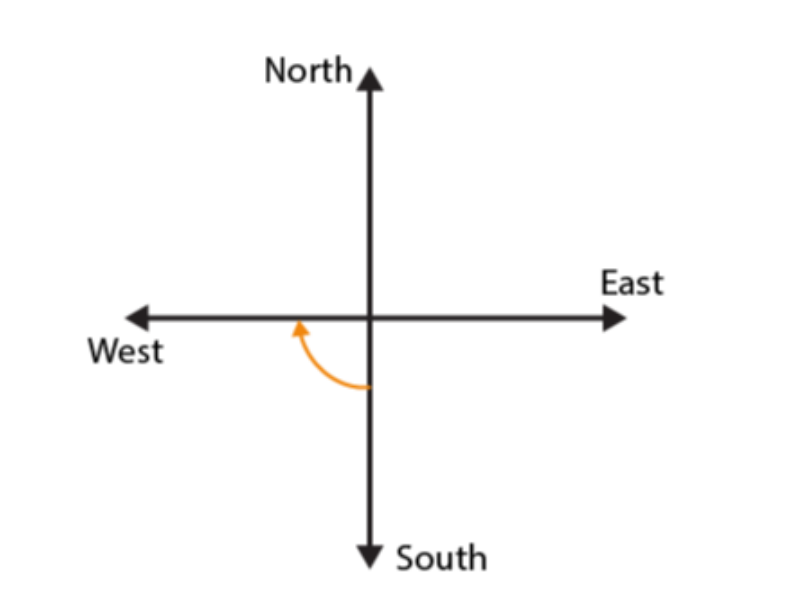 (b)
If we start facing towards North and turn anti-clockwise to East, we have to make 3 right angles
(b)
If we start facing towards North and turn anti-clockwise to East, we have to make 3 right angles
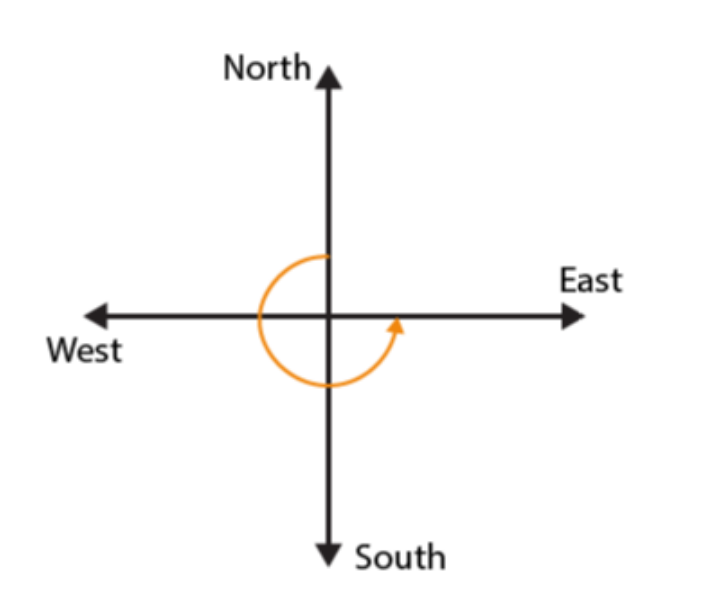 (c)
If we start facing towards West and turn to West, we have to make one complete round or 4 right angles
(c)
If we start facing towards West and turn to West, we have to make one complete round or 4 right angles
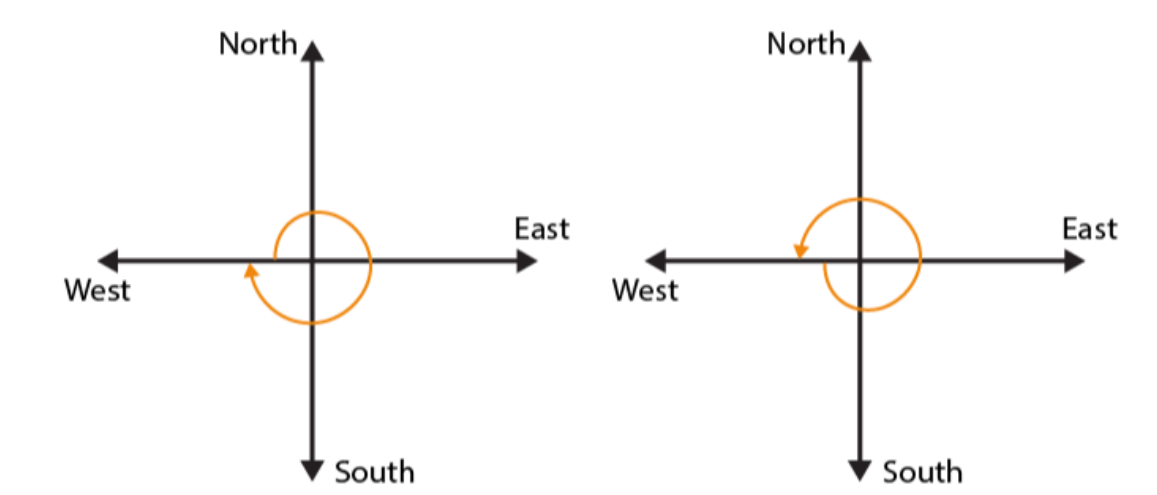 (d)
If we start facing towards South and turn to North, we have to make 2 right angles
(d)
If we start facing towards South and turn to North, we have to make 2 right angles
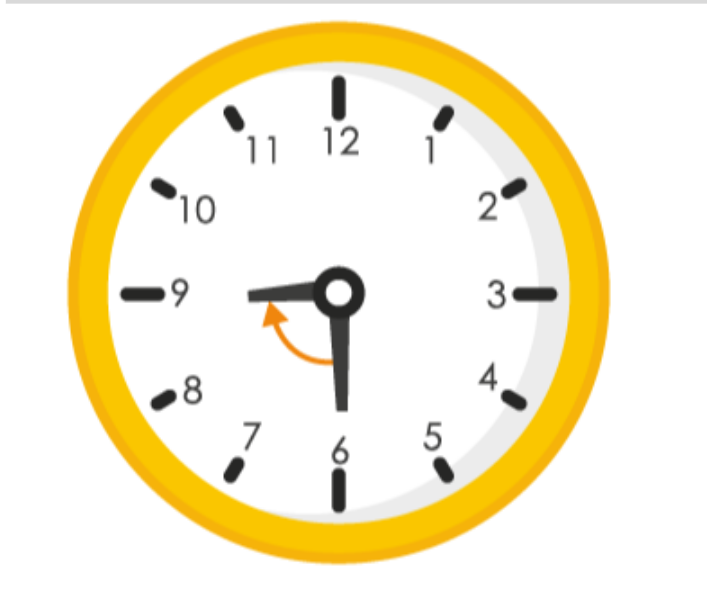
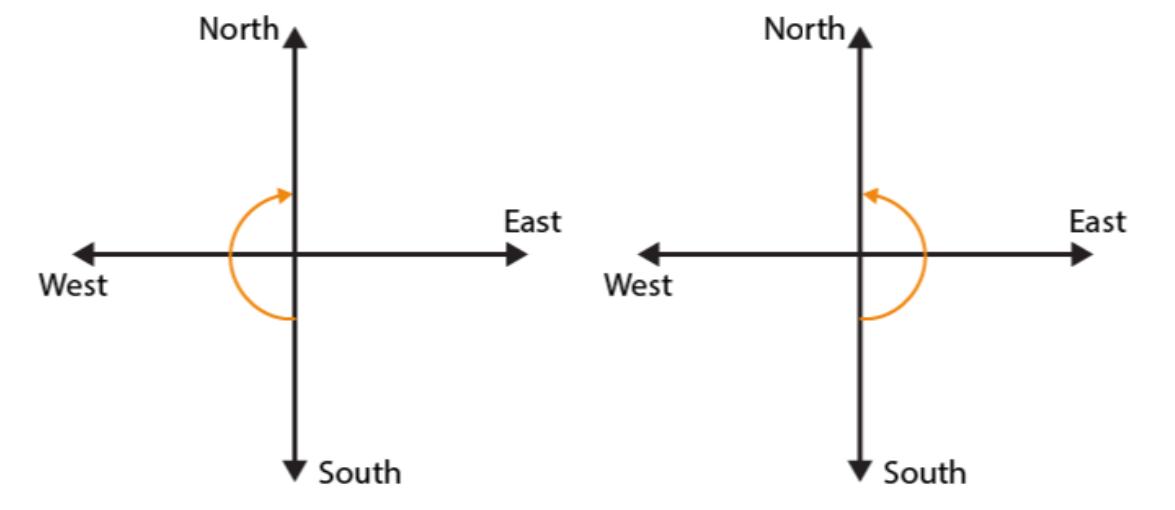 7. Where will the hour hand of a clock stop if it starts
(a) from 6 and turns through 1 right angle?
(b) from 8 and turns through 2 right angles?
(c) from 10 and turns through 3 right angles?
(d) from 7 and turns through 2 straight angles?
Solutions:
We know that in 1 complete revolution in either clockwise or anticlockwise direction, hour hand of a clock will rotate by 360
0
or 4 right angles
(a)
If hour hand of a clock starts from 6 and turns through 1 right angle, it will stop at 9
7. Where will the hour hand of a clock stop if it starts
(a) from 6 and turns through 1 right angle?
(b) from 8 and turns through 2 right angles?
(c) from 10 and turns through 3 right angles?
(d) from 7 and turns through 2 straight angles?
Solutions:
We know that in 1 complete revolution in either clockwise or anticlockwise direction, hour hand of a clock will rotate by 360
0
or 4 right angles
(a)
If hour hand of a clock starts from 6 and turns through 1 right angle, it will stop at 9
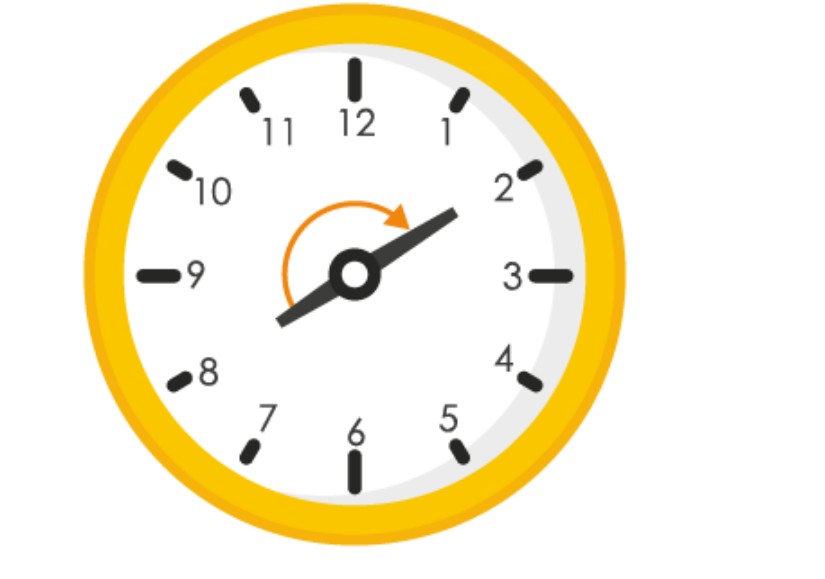
 (b)
If hour hand of a clock starts from 8 and turns through 2 right angles, it will stop at 2
(b)
If hour hand of a clock starts from 8 and turns through 2 right angles, it will stop at 2
 (c)
If hour hand of a clock starts from 10 and turns through 3 right angles, it will stop at 7
(c)
If hour hand of a clock starts from 10 and turns through 3 right angles, it will stop at 7
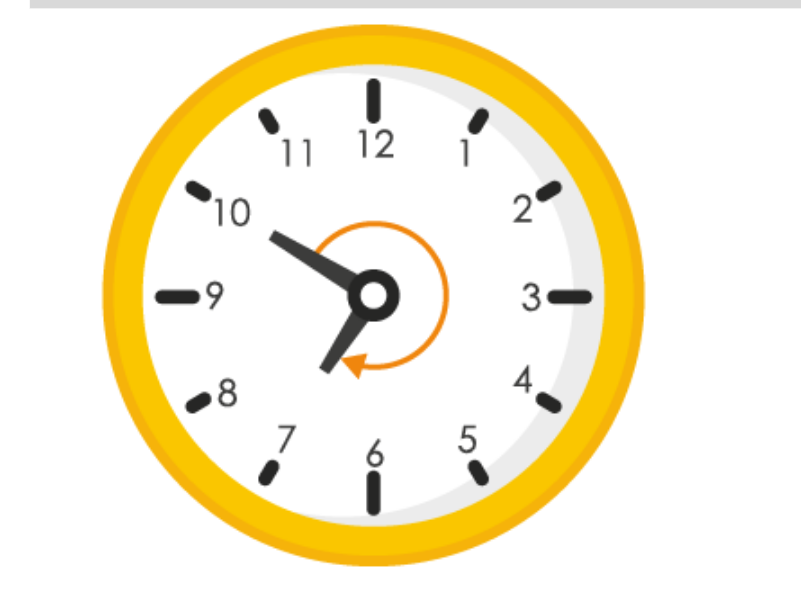 (d)
If hour hand of a clock starts from 7 and turns through 2 straight angles, it will stop at 7
(d)
If hour hand of a clock starts from 7 and turns through 2 straight angles, it will stop at 7
| CBSE Syllabus Class 6 | |
| CBSE Class 6 Science Syllabus | CBSE Class 6 Maths Syllabus |
| CBSE Class 6 Social Science Syllabus | CBSE Class 6 English Syllabus |
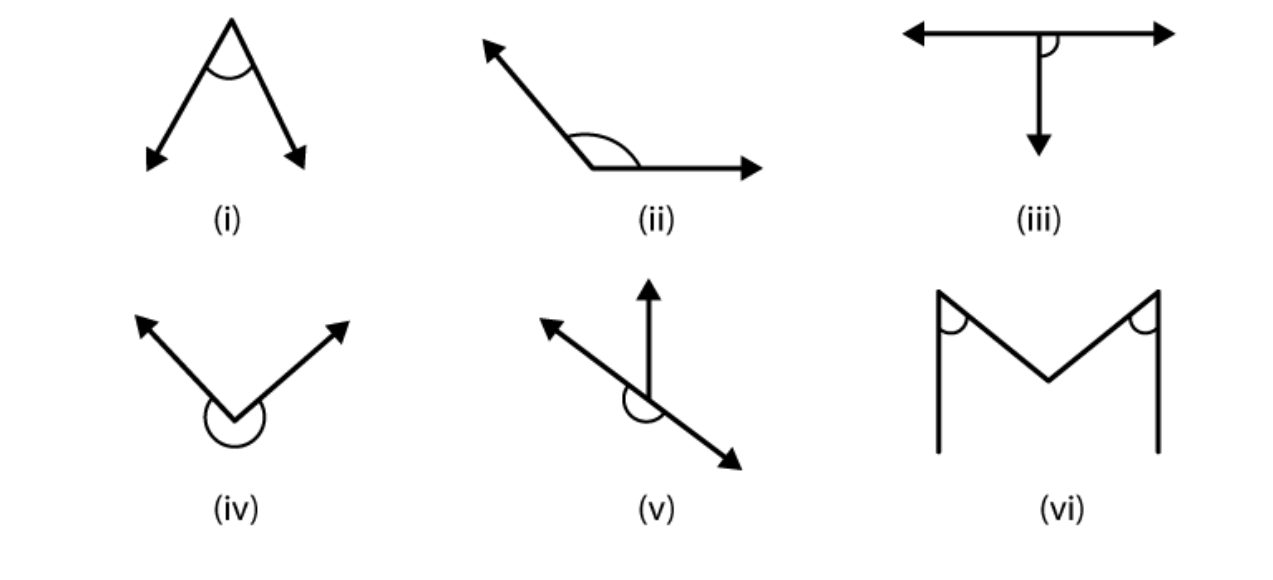 Solutions:
(i)
The given angle is acute angle it measures less than 90
0
(ii)
The given angle is obtuse angle as it measures more than 90
0
but less than 180
0
(iii)
The given angle is right angle as it measures 90
0
(iv)
The given angle is reflex angle as it measures more than 180
0
but less than 360
0
(v)
The given angle is straight angle as it measures 180
0
(vi)
The given angle is acute angle as it measures less than 90
0
Exercise 5.4 Page No: 97
1. What is the measure of
(i) a right angle
(ii) a straight angle
Solutions:
(i)
The measure of a right angle is 90
0
(ii)
The measure of a straight angle is 180
0
2. Say True or False:
(a) The measure of an acute angle < 90
0
(b) The measure of an obtuse angle < 90
0
(c) The measure of a reflex angle > 180
0
(d) The measure of one complete revolution = 360
0
(e) If m
∠
A = 53
0
and m
∠
B = 35
0
, then m
∠
A > m
∠
B.
Solutions:
(a)
True, the measure of an acute angle is less than 90
0
(b)
False, the measure of an obtuse angle is more than 90
0
but less than 180
0
(c)
True, the measure of a reflex angle is more than 180
0
(d)
True, the measure of one complete revolution is 360
0
(e)
True,
∠
A is greater than
∠
B
3. Write down the measures of
(a) some acute angles
(b) some obtuse angles
(give at least two examples of each)
Solutions:
(a)
The measures of an acute angle are 50
0
, 65
0
(b)
The measures of obtuse angle are 110
0
, 175
0
4. Measures the angles given below using the protractor and write down the measure.
Solutions:
(i)
The given angle is acute angle it measures less than 90
0
(ii)
The given angle is obtuse angle as it measures more than 90
0
but less than 180
0
(iii)
The given angle is right angle as it measures 90
0
(iv)
The given angle is reflex angle as it measures more than 180
0
but less than 360
0
(v)
The given angle is straight angle as it measures 180
0
(vi)
The given angle is acute angle as it measures less than 90
0
Exercise 5.4 Page No: 97
1. What is the measure of
(i) a right angle
(ii) a straight angle
Solutions:
(i)
The measure of a right angle is 90
0
(ii)
The measure of a straight angle is 180
0
2. Say True or False:
(a) The measure of an acute angle < 90
0
(b) The measure of an obtuse angle < 90
0
(c) The measure of a reflex angle > 180
0
(d) The measure of one complete revolution = 360
0
(e) If m
∠
A = 53
0
and m
∠
B = 35
0
, then m
∠
A > m
∠
B.
Solutions:
(a)
True, the measure of an acute angle is less than 90
0
(b)
False, the measure of an obtuse angle is more than 90
0
but less than 180
0
(c)
True, the measure of a reflex angle is more than 180
0
(d)
True, the measure of one complete revolution is 360
0
(e)
True,
∠
A is greater than
∠
B
3. Write down the measures of
(a) some acute angles
(b) some obtuse angles
(give at least two examples of each)
Solutions:
(a)
The measures of an acute angle are 50
0
, 65
0
(b)
The measures of obtuse angle are 110
0
, 175
0
4. Measures the angles given below using the protractor and write down the measure.
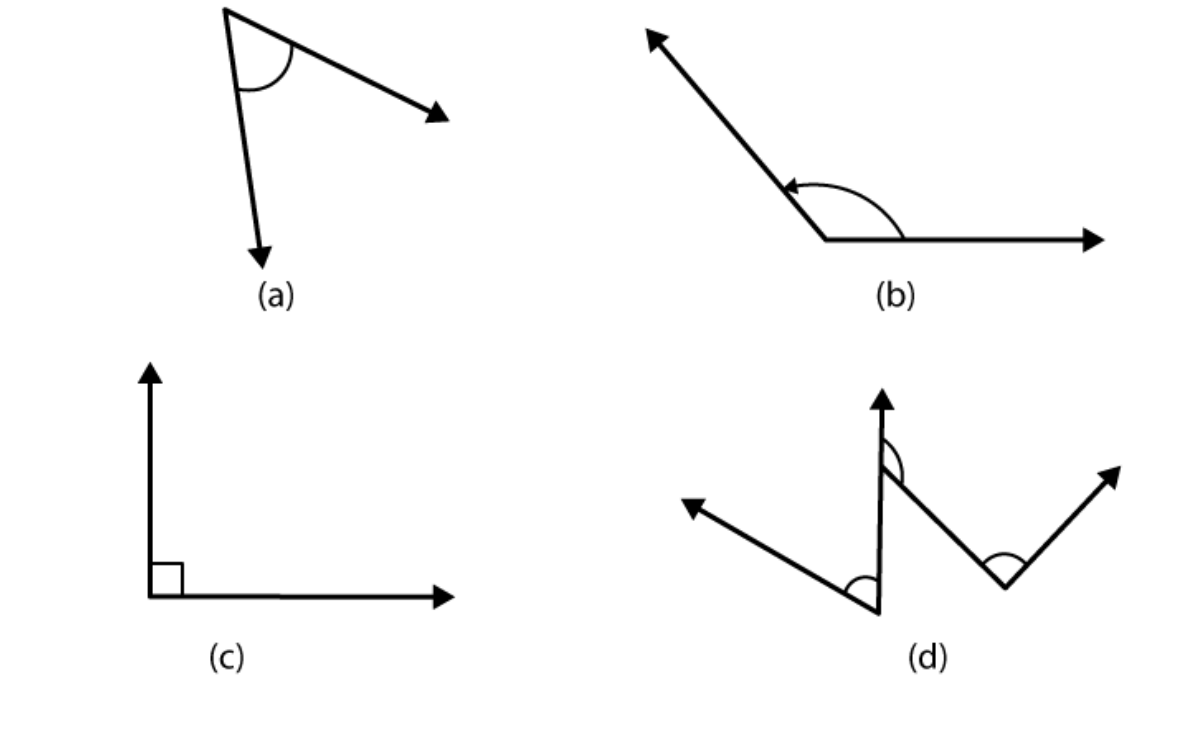 Solutions:
(a)
The measure of an angle is 45 degree
(b)
The measure of an angle is 120 degree
(c)
The measure of an angle is 90 degree
(d)
The measures of an angles are 60 degree
, 90 degree
and 130 degree
5. Which angle has a large measure? First estimate and then measure.
Measure of Angle A =
Measure of Angle B =
Solutions:
(a)
The measure of an angle is 45 degree
(b)
The measure of an angle is 120 degree
(c)
The measure of an angle is 90 degree
(d)
The measures of an angles are 60 degree
, 90 degree
and 130 degree
5. Which angle has a large measure? First estimate and then measure.
Measure of Angle A =
Measure of Angle B =
 Solutions:
The measure of angle A is 40 degree
The measure of angle B is 68 degree
∠
B has a large measure than
∠
A
6. From these two angles which has larger measure? Estimate and then confirm by measuring them.
Solutions:
The measure of angle A is 40 degree
The measure of angle B is 68 degree
∠
B has a large measure than
∠
A
6. From these two angles which has larger measure? Estimate and then confirm by measuring them.
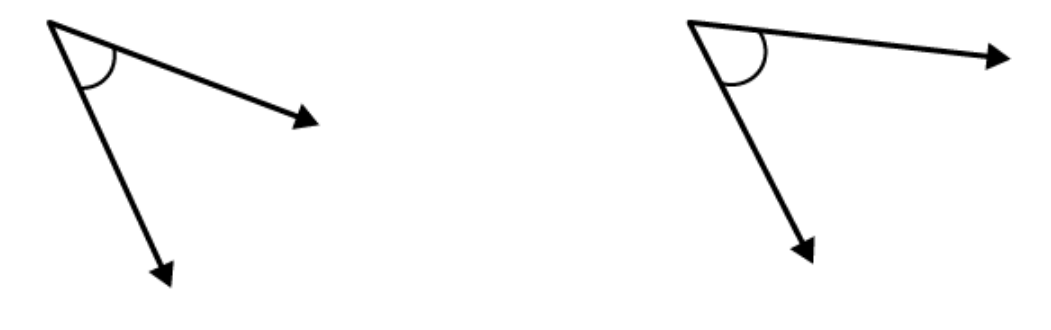 Solutions:
The measures of these angles are 45
0
and 55
0
. Hence, angle shown in second figure is greater.
7. Fill in the blanks with acute, obtuse, right or straight:
(a) An angle whose measure is less than that of a right angle is _____
(b) An angle whose measure is greater than that of a right angle is ____
(c) An angle whose measure is the sum of the measures of two right angles is _______
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is _____
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be ______
Solutions:
(a)
An angle whose measure is less than that of a right angle is acute angle
(b)
An angle whose measure is greater than that of a right angle is obtuse angle (but less than 180
0
)
(c)
An angle whose measure is the sum of the measures of two right angles is straight angle
(d)
When the sum of the measures of two angles is that of a right angle, then each one of them is acute angle
(e)
When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be obtuse angle.
8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor).
Solutions:
The measures of these angles are 45
0
and 55
0
. Hence, angle shown in second figure is greater.
7. Fill in the blanks with acute, obtuse, right or straight:
(a) An angle whose measure is less than that of a right angle is _____
(b) An angle whose measure is greater than that of a right angle is ____
(c) An angle whose measure is the sum of the measures of two right angles is _______
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is _____
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be ______
Solutions:
(a)
An angle whose measure is less than that of a right angle is acute angle
(b)
An angle whose measure is greater than that of a right angle is obtuse angle (but less than 180
0
)
(c)
An angle whose measure is the sum of the measures of two right angles is straight angle
(d)
When the sum of the measures of two angles is that of a right angle, then each one of them is acute angle
(e)
When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be obtuse angle.
8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor).
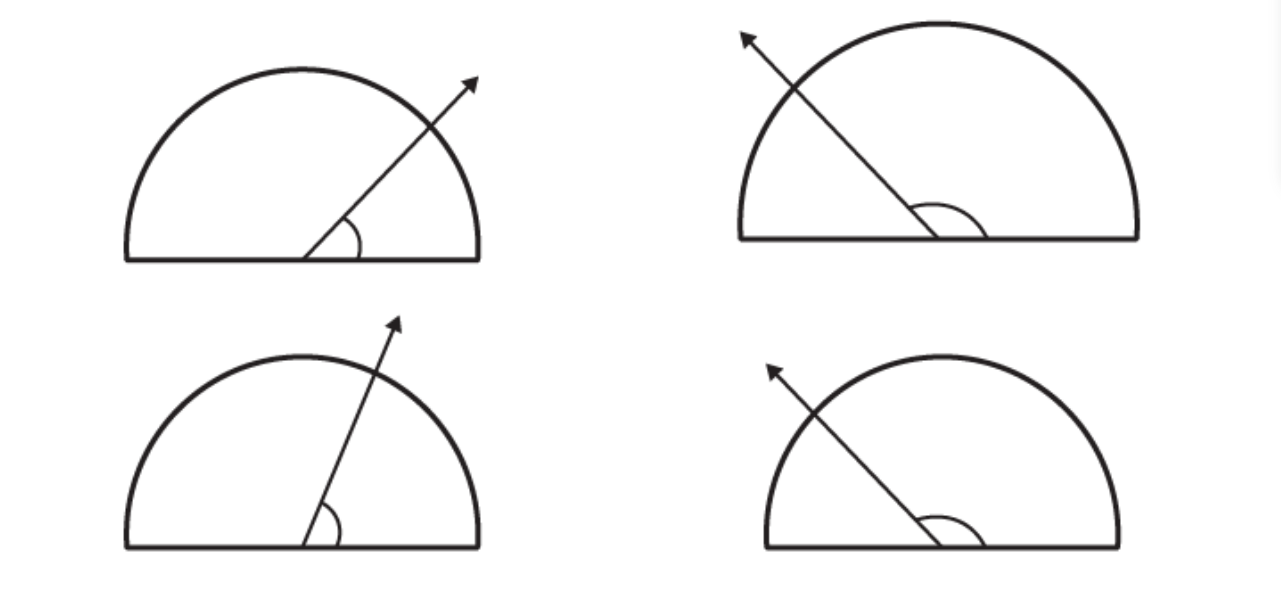 Solutions:
The measures of the angles shown in above figure are 40 degree
, 130 degree
, 65 degree
and 135 degree
9. Find the angle measure between the hands of the clock in each figure:
Solutions:
The measures of the angles shown in above figure are 40 degree
, 130 degree
, 65 degree
and 135 degree
9. Find the angle measure between the hands of the clock in each figure:
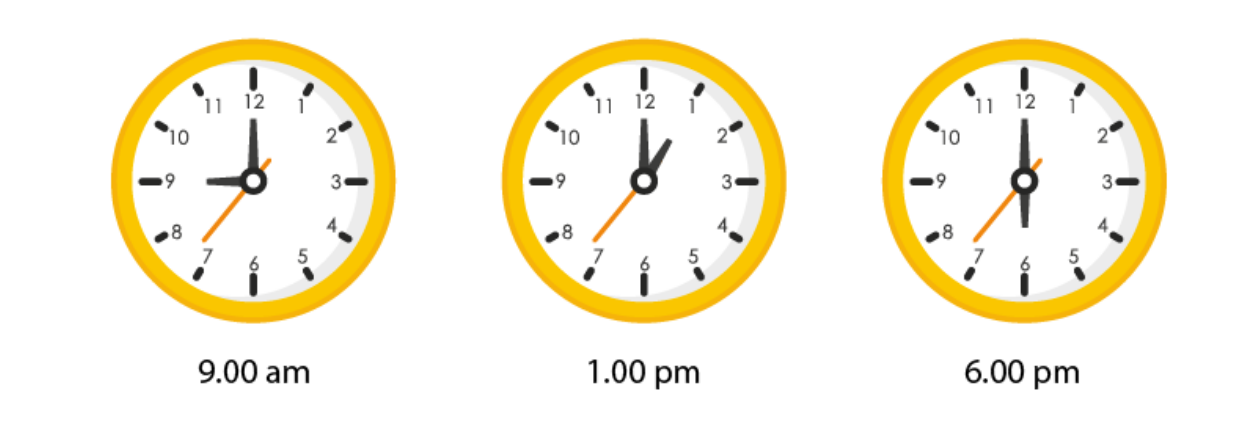 Solutions:
The angle measure between the hands of the clock are 90 degree
, 30 degree
and 180 degree
10. Investigate
In the given figure, the angle measure 30 degree
. Look at the same figure through a magnifying glass. Does the angle becomes larger? Does the size of the angle change?
Solutions:
The angle measure between the hands of the clock are 90 degree
, 30 degree
and 180 degree
10. Investigate
In the given figure, the angle measure 30 degree
. Look at the same figure through a magnifying glass. Does the angle becomes larger? Does the size of the angle change?
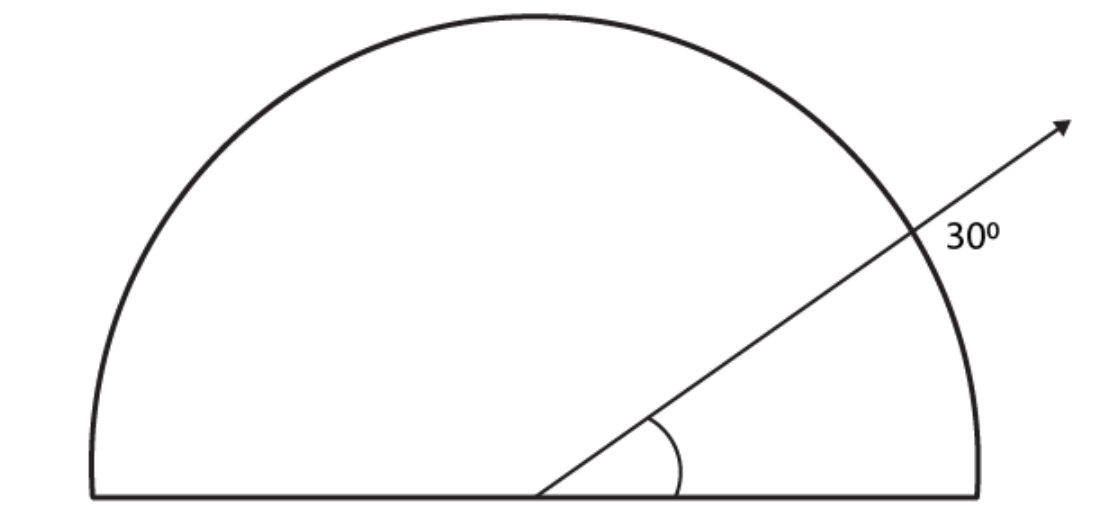 Solutions:
The measure of an angle will not change by viewing through a magnifying glass
11. Measure and classify each angle:
Solutions:
The measure of an angle will not change by viewing through a magnifying glass
11. Measure and classify each angle:
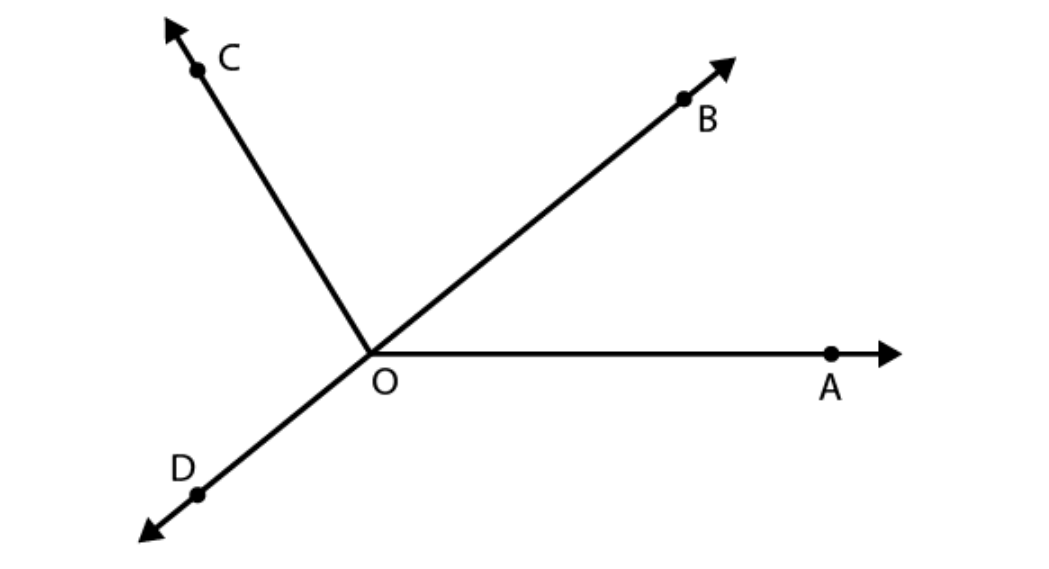
| Angle | Measure | Type |
| ∠ AOB | ||
| ∠ AOC | ||
| ∠ BOC | ||
| ∠ DOC | ||
| ∠ DOA | ||
| ∠ DOB |
| Angle | Measure | Type |
| ∠ AOB | 40 0 | Acute |
| ∠ AOC | 125 0 | Obtuse |
| ∠ BOC | 85 0 | Acute |
| ∠ DOC | 95 0 | Obtuse |
| ∠ DOA | 140 0 | Obtuse |
| ∠ DOB | 180 0 | Straight |
| Related Links |
NCERT Solutions for Class 6 Maths Chapter 5 FAQs
How can one gain a better understanding of chapter 5, Understanding Elementary Shapes?
To enhance comprehension, review key concepts, solve related problems, and utilize additional resources such as online tutorials.
What does Understanding Elementary Shapes mean?
Understanding Elementary Shapes involves acquiring knowledge about basic geometric figures, their properties, and relationships, as covered in educational curricula.
What are parallelograms?
Parallelograms are quadrilaterals with opposite sides parallel and equal in length, featuring properties such as equal opposite angles.
How should practical geometry be studied?
To study practical geometry effectively, engage in hands-on activities, use appropriate tools, and apply geometric principles to real-world situations.
What are the disadvantages of comparing line segments by tracing and by observation?
Comparing line segments by tracing can lead to inaccuracies, while observation may introduce human error, making both methods less reliable for precise measurements in geometry.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App







