NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State
NCERT Solutions for Class 12 Chemistry Chapter 1 contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in Chapter 1.
Krati Saraswat9 Apr, 2025
Share
NCERT Solutions for Class 12 Chemistry Chapter 1 (The Solid State)
NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid States of Chemistry is prepared by our senior and renowned teachers of Physics Wallah primary focus while solving these questions of class 12 in the NCERT textbook, also do read the theory of this NCERT solution for class 12 chemistry Chapter 1 The Solid States of Chemistry while going before solving the NCERT questions. Our Physics Wallah team Prepared Other Subjects NCERT Solutions for class 12.NCERT Solutions for Class 12 Chemistry Chapter 2
NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State Overview
NCERT Solutions for Class 12 Chemistry Chapter 1
Answer the following Questions of NCERT Solutions for Class 12 Chemistry Chapter 1:
Question 1. Name the parameters that characterize a unit cell. Solution : The six parameters that characterise a unit cell are as follows. (i) Its dimensions along the three edges, a, b, and c These edges may or may not be equal. (ii) Angles between the edges These are the angle ∝ (between edges b and c), β (between edges a and c), and γ (between edges a and b).NCERT Solutions for Class 12 Chemistry Chapter 3
Question 2. Distinguish between (i)Hexagonal and monoclinic unit cells (ii) Face-centred and end-centred unit cells.Solution : (i) Hexagonal unit cell For a hexagonal unit cell,
Monoclinic unit cell For a monoclinic cell, 
(ii) Face-centred unit cell In a face-centred unit cell, the constituent particles are present at the corners and one at the centre of each face. End-centred unit cell An end-centred unit cell contains particles at the corners and one at the centre of any two opposite faces.
Question 3. Explain how much portion of an atom located at (i) corner and (ii) body-centre of a cubic unit cell is part of its neighbouring unit cell.
Solution : (i)An atom located at the corner of a cubic unit cell is shared by eight adjacent unit cells.
Therefore, 1/8 th portion of the atom is shared by one unit cell. (ii)An atom located at the body centre of a cubic unit cell is not shared by its neighbouring unit cell. Therefore, the atom belongs only to the unit cell in which it is present i.e., its contribution to the unit cell is 1.
NCERT Solutions for Class 12 Chemistry Chapter 4
Question 4. What is the two dimensional coordination number of a molecule in square close packed layer?Solution : In square close-packed layer, a molecule is in contact with four of its neighbours. Therefore, the two-dimensional coordination number of a molecule in square close-packed layer is 4.
Question 5. A compound forms hexagonal close-packed structure.
What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?
Solution : Number of close-packed particles = 0.5 × 6.022 × 10 23 = 3.011 × 10 23 Therefore, number of octahedral voids = 3.011 × 10 23 And, number of tetrahedral voids = 2 × 3.011 × 10 23 = 6.022 ×10 23 Therefore, total number of voids = 3.011 × 10 23 + 6.022 × 10 23 = 9.033 × 10 23
Question 6. A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy 1/3 rd of tetrahedral voids.
What is the formula of the compound?
Solution : The ccp lattice is formed by the atoms of the element N. Here, the number of tetrahedral voids generated is equal to twice the number of atoms of the element N.
According to the question, the atoms of element M occupy 1/3 rd of the tetrahedral voids. Therefore, the number of atoms of M is equal to
of the number of atoms of N. Therefore, ratio of the number of atoms of M to that of N is M: N 
= 2 : 3 Thus, the formula of the compound is M 2 N 3 .
NCERT Solutions for Class 12 Chemistry Chapter 5
Question 7. Which of the following lattices has the highest packing efficiency (i) simple cubic (ii) body-centred cubic and (iii) hexagonal close-packed lattice?Solution : Hexagonal close-packed lattice has the highest packing efficiency of 74%. The packing efficiencies of simple cubic and body-centred cubic lattices are 52.4% and 68% respectively.
Question 8. An element with molar mass 2.7 × 10 -2 kg mol -1 forms a cubic unit cell with edge length 405 pm. If its density is 2.7 × 103 kg m −3 , what is the nature of the cubic unit cell?
Solution : It is given that density of the element, d = 2.7 × 10 3 kg m −3 Molar mass, M = 2.7 × 10 −2 kg mol −1 Edge length, a = 405 pm = 405 × 10 −12 m = 4.05 × 10 −10 m It is known that, Avogadro’s number, N A = 6.022 × 1023 mol −1 Applying the relation,
This implies that four atoms of the element are present per unit cell. Hence, the unit cell is face-centred cubic (fcc) or cubic close-packed (ccp).
Question 9. What type of defect can arise when a solid is heated? Which physical property is affected by it and in what way?
Solution : When a solid is heated, vacancy defect can arise. A solid crystal is said to have vacancy defect when some of the lattice sites are vacant. Vacancy defect leads to a decrease in the density of the solid.
Question 10. What type of stoichiometric defect is shown by: (i) ZnS (ii) AgBr
Solution : (i) ZnS shows Frenkel defect. (ii) AgBr shows Frenkel defect as well as Schottky defect.
Question 11. Explain how vacancies are introduced in an ionic solid when a cation of higher valence is added as an impurity in it.
Solution : When a cation of higher valence is added to an ionic solid as an impurity to it, the cation of higher valence replaces more than one cation of lower valence so as to keep the crystal electrically neutral. As a result, some sites become vacant. For example, when Sr 2+ is added to NaCl, each Sr 2+ ion replaces two Na + ions. However, one Sr 2+ ion occupies the site of one Na + ion and the other site remains vacant. Hence, vacancies are introduced.
Question 12. Ionic solids, which have anionic vacancies due to metal excess defect, develop colour. Explain with the help of a suitable example.
Solution : The colour develops because of the presence of electrons in the anionic sites. These electrons absorb energy from the visible part of radiation and get excited. For example, when crystals of NaCl are heated in an atmosphere of sodium vapours, the sodium atoms get deposited on the surface of the crystal and the chloride ions from the crystal diffuse to the surface to form NaCl with the deposited Na atoms. During this process, the Na atoms on the surface lose electrons to form Na + ions and the released electrons diffuse into the crystal to occupy the vacant anionic sites. These electrons get excited by absorbing energy from the visible light and impart yellow colour to the crystals.
Question 13. A group 14 element is to be converted into n-type semiconductor by doping it with a suitable impurity. To which group should this impurity belong?
Solution : An n-type semiconductor conducts because of the presence of extra electrons. Therefore, a group 14 element can be converted to n-type semiconductor by doping it with a group 15 element.
Question 14. What type of substances would make better permanent magnets, ferromagnetic or ferrimagnetic. Justify your answer.
Solution : Ferromagnetic substances would make better permanent magnets. In solid state, the metal ions of ferromagnetic substances are grouped together into small regions. These regions are called domains and each domain acts as a tiny magnet. In an unmagnetised piece of a ferromagnetic substance, the domains are randomly oriented. As a result, the magnetic moments of the domains get cancelled. However, when the substance is placed in a magnetic field, all the domains get oriented in the direction of the magnetic field and a strong magnetic effect is produced. The ordering of the domains persists even after the removal of the magnetic field. Thus, the ferromagnetic substance becomes a permanent magnet.
Question 15. Why are solids rigid?
Solution : The intermolecular forces of attraction that are present in solids are very strong. The constituent particles of solids cannot move from their positions i.e., they have fixed positions. However, they can oscillate about their mean positions. This is the reason solids are rigid. Question 16. Why do solids have a definite volume? Solution : The intermolecular forces of attraction that are present in solids are very strong. The constituent particles of solids have fixed positions i.e., they are rigid. Hence, solids have a definite volume. Question 17. Classify the following as amorphous or crystalline solids: Polyurethane, naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, polyvinyl chloride, fibre glass, copper. Solution : Amorphous solids Polyurethane, teflon, cellophane, polyvinyl chloride, fibre glass Crystalline solids Naphthalene, benzoic acid, potassium nitrate, copper Question 18. Why is glass considered a super cooled liquid? Solution : Similar to liquids, glass has a tendency to flow, though very slowly. Therefore, glass is considered as a super cooled liquid. This is the reason that glass windows and doors are slightly thicker at the bottom than at the top. Question 19. Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of this solid. Would it show cleavage property? Solution : An isotropic solid has the same value of physical properties when measured along different directions. Therefore, the given solid, having the same value of refractive index along all directions, is isotropic in nature. Hence, the solid is an amorphous solid. When an amorphous solid is cut with a sharp edged tool, it cuts into two pieces with irregular surfaces. Question 20. Classify the following solids in different categories based on the nature of intermolecular forces operating in them: Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide. Solution : Potassium sulphate → Ionic solid Tin → Metallic solid Benzene → Molecular (non-polar) solid Urea → Polar molecular solid Ammonia → Polar molecular solid Water → Hydrogen bonded molecular solid Zinc sulphide → Ionic solid Graphite → Covalent or network solid Rubidium → Metallic solid Argon → Non-polar molecular solid Silicon carbide → Covalent or network solid Question 21. Solid A is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it? Solution : The given properties are the properties of a covalent or network solid. Therefore, the given solid is a covalent or network solid. Examples of such solids include diamond (C) and quartz (SiO 2 ). Question 22. Ionic solids conduct electricity in molten state but not in solid state. Explain. Solution : In ionic compounds, electricity is conducted by ions. In solid state, ions are held together by strong electrostatic forces and are not free to move about within the solid. Hence, ionic solids do not conduct electricity in solid state. However, in molten state or in solution form, the ions are free to move and can conduct electricity. Question 23. What type of solids are electrical conductors, malleable and ductile? Solution : Metallic solids are electrical conductors, malleable, and ductile. Question 24. Give the significance of a ‘lattice point’. Solution : The significance of a lattice point is that each lattice point represents one constituent particle of a solid which may be an atom, a molecule (group of atom), or an ion. Question 25. What is a semiconductor? Describe the two main types of semiconductors and contrast their conduction mechanism. Solution : Semiconductors are substances having conductance in the intermediate range of 10 -6 to 10 4 ohm −1 m −1 . The two main types of semiconductors are: (i) n-type semiconductor (ii) p-type semiconductor n-type semiconductor: The semiconductor whose increased conductivity is a result of negatively-charged electrons is called an n-type semiconductor. When the crystal of a group 14 element such as Si or Ge is doped with a group 15 element such as P or As, an n-type semiconductor is generated. Si and Ge have four valence electrons each. In their crystals, each atom forms four covalent bonds. On the other hand, P and As contain five valence electrons each. When Si or Ge is doped with P or As, the latter occupies some of the lattice sites in the crystal. Four out of five electrons are used in the formation of four covalent bonds with four neighbouring Si or Ge atoms. The remaining fifth electron becomes delocalised and increases the conductivity of the doped Si or Ge.
p-type semiconductor: The semiconductor whose increased in conductivity is a result of electron hole is called a p-type semiconductor. When a crystal of group 14 elements such as Si or Ge is doped with a group 13 element such as B, Al, or Ga (which contains only three valence electrons), a p-type of semiconductor is generated. When a crystal of Si is doped with B, the three electrons of B are used in the formation of three covalent bonds and an electron hole is created. An electron from the neighbouring atom can come and fill this electron hole, but in doing so, it would leave an electron hole at its original position. The process appears as if the electron hole has moved in the direction opposite to that of the electron that filled it. Therefore, when an electric field is applied, electrons will move toward the positively-charged plate through electron holes. However, it will appear as if the electron holes are positively-charged and are moving toward the negatively- charged plate. 
Question 26. Non-stoichiometric cuprous oxide, Cu 2 O can be prepared in laboratory. In this oxide, copper to oxygen ratio is slightly less than 2:1. Can you account for the fact that this substance is a p-type semiconductor? Solution : In the cuprous oxide (Cu 2 O) prepared in the laboratory, copper to oxygen ratio is slightly less than 2:1. This means that the number of Cu + ions is slightly less than twice the number of O 2− ions. This is because some Cu + ions have been replaced by Cu 2+ ions. Every Cu 2+ ion replaces two Cu + ions, thereby creating holes. As a result, the substance conducts electricity with the help of these positive holes. Hence, the substance is a p-type semiconductor. Question 27. Ferric oxide crystallises in a hexagonal close-packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of the ferric oxide. Solution : Let the number of oxide (O 2− ) ions be x. So, number of octahedral voids = x It is given that two out of every three octahedral holes are occupied by ferric ions. So, number of ferric (Fe 3+ ) ions = 2/3x Therefore, ratio of the number of Fe 3+ ions to the number of O 2− ions, Fe 3+ : O 2− = 2/3x:x 2/3 :1 =2:3 = 2 : 3 Hence, the formula of the ferric oxide is Fe 2 O 3 . Question 28.Classify each of the following as being either a p-type or an n-type semiconductor: (i) Ge doped with In (ii) B doped with Si. Solution : (i) Ge (a group 14 element) is doped with In (a group 13 element). Therefore, a hole will be created and the semiconductor generated will be a p-type semiconductor. (ii) B (a group 13 element) is doped with Si (a group 14 element). Thus, a hole will be created and the semiconductor generated will be a p-type semiconductor. Question 29. Gold (atomic radius = 0.144 nm) crystallises in a face-centred unit cell. What is the length of a side of the cell? Solution : For a face-centred unit cell: a = 2 √2r It is given that the atomic radius, r = 0.144 nm So, a = 2 √2 × 0.144 nm = 0.407 nm Hence, length of a side of the cell = 0.407 nm Question 30. In terms of band theory, what is the difference (i) Between a conductor and an insulator (ii) Between a conductor and a semiconductor Solution : (i) The valence band of a conductor is partially-filled or it overlaps with a higher energy, unoccupied conduction band. 
On the other hand, in the case of an insulator, the valence band is fully- filled and there is a large gap between the valence band and the conduction band. (ii) In the case of a conductor, the valence band is partially-filled or it overlaps with a higher energy, unoccupied conduction band. So, the electrons can flow easily under an applied electric field. 
On the other hand, the valence band of a semiconductor is filled and there is a small gap between the valence band and the next higher conduction band. Therefore, some electrons can jump from the valence band to the conduction band and conduct electricity. Question 31. Explain the following terms with suitable examples: (i) Schottky defect (ii) Frenkel defect (iii) Interstitials and (iv) F-centres Solution : (i) Schottky defect: Schottky defect is basically a vacancy defect shown by ionic solids. In this defect, an equal number of cations and anions are missing to maintain electrical neutrality. It decreases the density of a substance. Significant number of Schottky defects is present in ionic solids. For example, in NaCl, there are approximately 10 6 Schottky pairs per cm 3 at room temperature. Ionic substances containing similar-sized cations and anions show this type of defect. For example: NaCl, KCl, CsCl, AgBr, etc. 
(ii) Frenkel defect: Ionic solids containing large differences in the sizes of ions show this type of defect. When the smaller ion (usually cation) is dislocated from its normal site to an interstitial site, Frenkel defect is created. It creates a vacancy defect as well as an interstitial defect. Frenkel defect is also known as dislocation defect. Ionic solids such as AgCl, AgBr, AgI, and ZnS show this type of defect. 
(iii) Interstitials: Interstitial defect is shown by non-ionic solids. This type of defect is created when some constituent particles (atoms or molecules) occupy an interstitial site of the crystal. The density of a substance increases because of this defect. 
(iv) F-centres: When the anionic sites of a crystal are occupied by unpaired electrons, the ionic sites are called F-centres. These unpaired electrons impart colour to the crystals. For example, when crystals of NaCl are heated in an atmosphere of sodium vapour, the sodium atoms are deposited on the surface of the crystal. The Cl ions diffuse from the crystal to its surface and combine with Na atoms, forming NaCl. During this process, the Na atoms on the surface of the crystal lose electrons. These released electrons diffuse into the crystal and occupy the vacant anionic sites, creating F-centres. 
Question 32. Aluminium crystallises in a cubic close-packed structure. Its metallic radius is 125 pm. (i) What is the length of the side of the unit cell? (ii) How many unit cells are there in 1.00 cm 3 of aluminium? Solution : (i) For cubic close-packed structure: a = 2 √2r = 2 √2 × 125 pm = 353.55 pm = 354 pm (approximately) (ii) Volume of one unit cell = (354 pm) 3 = 4.4 × 10 7 pm 3 = 4.4 × 10 7 × 10 −30 cm 3 = 4.4 × 10 −23 cm 3 Therefore, number of unit cells in 1.00 cm 3 = 
= 2.27 × 10 22 Question 33. If NaCl is doped with 10 −3 mol % of SrCl 2 , what is the concentration of cation vacancies? Solution : It is given that NaCl is doped with 10 −3 mol% of SrCl 2 . This means that 100 mol of NaCl is doped with 10 −3 mol of SrCl 2 . Therefore, 1 mol of NaCl is doped with 
mol of SrCl 2 = 10 −5 mol of SrCl 2 Cation vacancies produced by one Sr 2+ ion = 1 
Hence, the concentration of cation vacancies created by SrCl 2 is 6.022 × 10 8 per mol of NaCl. Question 34. Explain the following with suitable examples: (i) Ferromagnetism (ii)Paramagnetism (iii)Ferrimagnetism (iv)Antiferromagnetism (v)12-16 and 13-15 group compounds. Solution : (i) Ferromagnetism: The substances that are strongly attracted by a magnetic field are called ferromagnetic substances. Ferromagnetic substances can be permanently magnetised even in the absence of a magnetic field. Some examples of ferromagnetic substances are iron, cobalt, nickel, gadolinium, and CrO 2 . In solid state, the metal ions of ferromagnetic substances are grouped together into small regions called domains and each domain acts as a tiny magnet. In an un-magnetised piece of a ferromagnetic substance, the domains are randomly-oriented and so, their magnetic moments get cancelled. However, when the substance is placed in a magnetic field, all the domains get oriented in the direction of the magnetic field. As a result, a strong magnetic effect is produced. This ordering of domains persists even after the removal of the magnetic field. Thus, the ferromagnetic substance becomes a permanent magnet. 
Schematic alignment of magnetic moments in ferromagnetic substances (ii) Paramagnetism: The substances that are attracted by a magnetic field are called paramagnetic substances. Some examples of paramagnetic substances are O 2 , Cu 2t , Fe 3t , and Cr 3t . Paramagnetic substances get magnetised in a magnetic field in the same direction, but lose magnetism when the magnetic field is removed. To undergo paramagnetism, a substance must have one or more unpaired electrons. This is because the unpaired electrons are attracted by a magnetic field, thereby causing paramagnetism. (iii) Ferrimagnetism: The substances in which the magnetic moments of the domains are aligned in parallel and anti-parallel directions, in unequal numbers, are said to have ferrimagnetism. Examples include Fe 3 O 4 (magnetite), ferrites such as MgFe 2 O 4 and ZnFe 2 O 4 . Ferrimagnetic substances are weakly attracted by a magnetic field as compared to ferromagnetic substances. On heating, these substances become paramagnetic. 
Schematic alignment of magnetic moments in ferrimagnetic substances (iv) Antiferromagnetism: Antiferromagnetic substanceshave domain structures similar to ferromagnetic substances, but are oppositely-oriented. The oppositely-oriented domains cancel out each other’s magnetic moments. 
Schematic alignment of magnetic moments in antiferromagnetic substances (v) 12-16 and 13-15 group compounds: The 12-16 group compounds are prepared by combining group 12 and group 16 elements and the 13-15 group compounds are prepared by combining group 13 and group15 elements. These compounds are prepared to stimulate average valence of four as in Ge or Si. Indium (III) antimonide (IrSb), aluminium phosphide (AlP), and gallium arsenide (GaAS) are typical compounds of groups 13-15. GaAs semiconductors have a very fast response time and have revolutionised the designing of semiconductor devices. Examples of group 12-16 compounds include zinc sulphide (ZnS), cadmium sulphide (CdS), cadmium selenide (CdSe), and mercury (II) telluride (HgTe). The bonds in these compounds are not perfectly covalent. The ionic character of the bonds depends on the electronegativities of the two elements. Question 35. Define the term 'amorphous'. Give a few examples of amorphous solids. Solution : Amorphous solids are the solids whose constituent particles are of irregular shapes and have short range order. These solids are isotropic in nature and melt over a range of temperature. Therefore, amorphous solids are sometimes called pseudo solids or super cooled liquids. They do not have definite heat of fusion. When cut with a sharp-edged tool, they cut into two pieces with irregular surfaces. Examples of amorphous solids include glass, rubber, and plastic. Question 36. What makes a glass different from a solid such as quartz? Under what conditions could quartz be converted into glass? Solution : The arrangement of the constituent particles makes glass different from quartz. In glass, the constituent particles have short range order, but in quartz, the constituent particles have both long range and short range orders. Quartz can be converted into glass by heating and then cooling it rapidly. Question 37. Classify each of the following solids as ionic, metallic, molecular, network (covalent) or amorphous. (i) Tetra phosphorus decoxide (P 4 O 10 ) (vii) Graphite (ii) Ammonium phosphate (NH4) 3 PO 4 (viii) Brass (iii) SiC (ix) Rb (iv) I 2 (x) LiBr (v) P 4 (xi) Si Solution : Ionic → (ii) Ammonium phosphate (NH 4 ) 3 PO 4 , (x) LiBr Metallic → (viii) Brass, (ix) Rb Molecular → (i) Tetra phosphorus decoxide (P 4 O 10 ), (iv) I 2 , (v) P 4 . Covalent (network) → (iii) SiC, (vii) Graphite, (xi) Si Amorphous → (vi) Plastic Question 38. (i) What is meant by the term 'coordination number'? (ii) What is the coordination number of atoms: (a) in a cubic close-packed structure? (b) in a body-centred cubic structure? Solution : (i) The number of nearest neighbours of any constituent particle present in the crystal lattice is called its coordination number. (ii) The coordination number of atoms (a) in a cubic close-packed structure is 12, and (b) in a body-centred cubic structure is 8 Question 39. How can you determine the atomic mass of an unknown metal if you know its density and the dimension of its unit cell? Explain. Solution : By knowing the density of an unknown metal and the dimension of its unit cell, the atomic mass of the metal can be determined. Let ‘a’ be the edge length of a unit cell of a crystal, ‘d’ be the density of the metal, ‘m’ be the mass of one atom of the metal and ‘z’ be the number of atoms in the unit cell. Now, density of the unit cell 
⇒ d =zm / a 3----------------------------(1) [Since mass of the unit cell = Number of atoms in the unit cell × mass of one atom] [Volume of the unit cell = (Edge length of the cubic unit cell) 3 ] From equation (i), we have: m = da 3 /z -----------------------------------------(ii) Now, mass of one atom of metal (m) 
Therefore, 
If the edge lengths are different (say a, b and c), then equation (ii) becomes: M = d(abc)NAz (iv) From equations (iii) and (iv), we can determine the atomic mass of the unknown metal. Question 40. 'Stability of a crystal is reflected in the magnitude of its melting point'. Comment. Collect melting points of solid water, ethyl alcohol, diethyl ether and methane from a data book. What can you say about the intermolecular forces between these molecules? Solution : Higher the melting point, greater is the intermolecular force of attraction and greater is the stability. A substance with higher melting point is more stable than a substance with lower melting point. The melting points of the given substances are: Solid water → 273 K Ethyl alcohol → 158.8 K Diethyl ether → 156.85 K Methane → 89.34 K Now, on observing the values of the melting points, it can be said that among the given substances, the intermolecular force in solid water is the strongest and that in methane is the weakest. Question 41. How will you distinguish between the following pairs of terms: (i) Hexagonal close-packing and cubic close-packing? (ii) Crystal lattice and unit cell? (iii) Tetrahedral void and octahedral void? Solution : (a) Cubic close packing: When a third layer is placed over the second layer in a manner that the octahedral voids are covered by the spheres, a layer different from the first (A) and second (B) is obtained. If we continue packing in this manner we get the cubic close packing. Hexagonal close packing: When the third layer is placed over the second layer in a way that the tetrahedral voids are covered by the spheres, a 3D close packing is produced where spheres in each third or alternate layers are vertically aligned. If we continue packing in this order we get hexagonal close packing. (b) Unit cell: It is the smallest 3D dimensional portion of a complete space lattice, which when repeated over and over again in different directions from the crystal lattice. Crystal lattice : it is a regular orientation of particles of a crystal in a 3D space. (c) Octahedral void : it is a void surrounded by 6 spheres. Tetrahedral void : it is a void surrounded by 4 spheres. 
Question 42. Find the packing efficiency of a metal crystal for : (a) simple cubic (b) body-centered cubic (c) face-centred cubic (with the assumptions that atoms are touching each other). Solution : (a) Simple cubic: In a simple cubic lattice, particles are present only at the corners and they touch each other along the edge. 
Let ,the edge length = a Radius of each particle = r. Thus, a = 2r Volume of spheres = πr 3 (4/3) Volume of a cubic unit cell = a 3 = (2r) 3 = 8r 3 We know that the number of particles per unit cell is 1. Therefore, Packing efficiency = Volume of one particle/Volume of cubic unit cell = [ πr 3 (4/3) ] / 8r 3 = 0.524 or 52.4 % (b) Body-centred cubic: 
From ∆FED, we have: b 2 = 2a 2 b = ( 2a ) 1/2 Again, from ∆AFD, we have : c 2 = a 2 + b 2 => c 2 = a 2 + 2a 2 c 2 = 3a 2 => c = (3a) 1/2 Let the radius of the atom = r. Length of the body diagonal, c = 4r => (3a) 1/2 = 4r => a = 4r/ (3) 1/2 or , r = [ a (3) 1/2 ]/ 4 Volume of the cube, a 3 = [4r/ (3) 1/2 ] 3 A BCC lattice has 2 atoms. So, volume of the occupied cubic lattice = 2πr 3 (4/3) = πr 3 ( 8/3) Therefore, packing efficiency = [ πr 3 ( 8/3) ]/ [ { 4r/(3) 1/2 } 3 ] = 0.68 or 68% (iii) Face-centred cubic: 
Let the edge length of the unit cell = a let the radius of each sphere = r Thus, AC = 4r From the right angled triangle ABC, we have : AC = ( a 2 + a 2 ) 1/2 = a(2) 1/2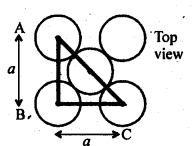 
Therefore, 4r = a(2) 1/2 => a = 4r/( 2) 1/2 Thus, Volume of unit cell =a 3 = { 4r/( 2) 1/2 } 3 a 3 = 64r 3 /2(2) 1/2 = 32r 3 / (2) 1/2 No. of unit cell in FCC = 4 Volume of four spheres = 4 × πr 3 (4/3) Thus, packing efficiency = [πr 3 (16/3) ] / [32r 3 / (2) 1/2 ] = 0.74 or 74 % Question 43. Explain (i) The basis of similarities and differences between metallic and ionic crystals. (ii) Ionic solids are hard and brittle. Solution : (i) The basis of similarities between metallic and ionic crystals is that both these crystal types are held by the electrostatic force of attraction. In metallic crystals, the electrostatic force acts between the positive ions and the electrons. In ionic crystals, it acts between the oppositely-charged ions. Hence, both have high melting points. The basis of differences between metallic and ionic crystals is that in metallic crystals, the electrons are free to move and so, metallic crystals can conduct electricity. However, in ionic crystals, the ions are not free to move. As a result, they cannot conduct electricity. However, in molten state or in aqueous solution, they do conduct electricity. (ii) The constituent particles of ionic crystals are ions. These ions are held together in three-dimensional arrangements by the electrostatic force of attraction. Since the electrostatic force of attraction is very strong, the charged ions are held in fixed positions. This is the reason why ionic crystals are hard and brittle. Question 44. Calculate the efficiency of packing in case of a metal crystal for (i) simple cubic (ii) body-centred cubic (iii) face-centred cubic (with the assumptions that atoms are touching each other). Solution : (i) Simple cubic In a simple cubic lattice, the particles are located only at the corners of the cube and touch each other along the edge. 
Let the edge length of the cube be ‘a’ and the radius of each particle be r. So, we can write: a = 2r Now, volume of the cubic unit cell = a 3 = (2r) 3 = 8r 3 We know that the number of particles per unit cell is 1. Therefore, volume of the occupied unit cell 
Hence, packing efficiency 
(ii) Body-centred cubic 
It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged. From ΔFED, we have: 
Again, from ΔAFD, we have: 
Let the radius of the atom be r. Length of the body diagonal, c = 4π 
or,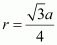 
Volume of the cube, 
A body-centred cubic lattice contains 2 atoms. So, volume of the occupied cubic lattice 
(iii) Face-centred cubic Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b. 
From ΔABC, we have: 
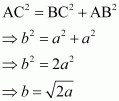Let r be the radius of the atom. Now, from the figure, it can be observed that: 
Now, volume of the cube, 
We know that the number of atoms per unit cell is 4. So, volume of the occupied unit cell 
= 74% Question 45. Silver crystallises in fcc lattice. If edge length of the cell is 4.07 × 10 −8 cm and density is 10.5 g cm −3 , calculate the atomic mass of silver. Solution : It is given that the edge length, a = 4.077 × 10 −8 cm Density, d = 10.5 g cm −3 As the lattice is fcc type, the number of atoms per unit cell, z = 4 We also know that, N A = 6.022 × 10 23 mol −1 Using the relation: 
= 107.13 gmol −1 Therefore, atomic mass of silver = 107.13 u Question 46. A cubic solid is made of two elements P and Q. Atoms of Q are at the corners of the cube and P at the body-centre. What is the formula of the compound? What are the coordination numbers of P and Q? Solution : It is given that the atoms of Q are present at the corners of the cube. Therefore, number of atoms of Q in one unit cell 
It is also given that the atoms of P are present at the body-centre. Therefore, number of atoms of P in one unit cell = 1 This means that the ratio of the number of P atoms to the number of Q atoms, P:Q = 1:1 Hence, the formula of the compound is PQ. The coordination number of both P and Q is 8. Question 47. Niobium crystallises in body-centred cubic structure. If density is 8.55 g cm −3 , calculate atomic radius of niobium using its atomic mass 93 u. Solution : It is given that the density of niobium, d = 8.55 g cm −3 Atomic mass, M = 93 gmol −1 As the lattice is bcc type, the number of atoms per unit cell, z = 2 We also know that, N A = 6.022 × 10 23 mol −1 Applying the relation: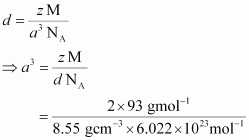 
= 3.612 × 10 −23 cm 3 So, a = 3.306 × 10 −8 cm For body-centred cubic unit cell: 
= 1.432 × 10 −8 cm = 14.32 × 10 −9 cm = 14.32 nm Question 48. If the radius of the octachedral void is r and radius of the atoms in close packing is R, derive relation between r and R. Solution : 
A sphere with centre O, is fitted into the octahedral void as shown in the above figure. It can be observed from the figure that ΔPOQ is right-angled ∠POQ = 90 0 Now, applying Pythagoras theorem, we can write: 
Question 49. Copper crystallises into a fcc lattice with edge length 3.61 × 10 −8 cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm −3 . Solution : Edge length, a = 3.61 × 10 −8 cm As the lattice is fcc type, the number of atoms per unit cell, z = 4 Atomic mass, M = 63.5 g mol −1 We also know that, NA = 6.022 × 10 23 mol −1 Applying the relation: 
= 8.97 g cm −3 The measured value of density is given as 8.92 g cm −3 . Hence, the calculated density 8.97 g cm −3 is in agreement with its measured value. Question 50. Analysis shows that nickel oxide has the formula Ni 0.98 O 1.00 . What fractions of nickel exist as Ni 2+ and Ni 3+ ions? Solution : The formula of nickel oxide is Ni 0.98 O 1.00 . Therefore, the ratio of the number of Ni atoms to the number of O atoms, Ni : O = 0.98 : 1.00 = 98 : 100 Now, total charge on 100 O 2− ions = 100 × (−2) = −200 Let the number of Ni 2+ ions be x. So, the number of Ni 3+ ions is 98 − x. Now, total charge on Ni 2+ ions = x(+2) = +2x And, total charge on Ni 3+ ions = (98 − x)(+3) = 294 − 3x Since, the compound is neutral, we can write: 2x + (294 − 3x) + (−200) = 0 ⇒ −x + 94 = 0 ⇒ x = 94 Therefore, number of Ni 2+ ions = 94 And, number of Ni 3+ ions = 98 − 94 = 4 Hence, fraction of nickel that exists as Ni 2+ = 94 / 98 = 0.959 And, fraction of nickel that exists as Ni 3+ = 4/98 = 0.041 Alternatively, fraction of nickel that exists as Ni 3+ = 1 − 0.959 = 0.041
NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State FAQs
Are NCERT Solutions for Class 12 Chemistry Chapter 1 helpful for board exams?
Yes, these solutions are crafted to help students prepare effectively for their board exams. They provide detailed explanations and step-by-step solutions to all the questions from the NCERT textbook, ensuring thorough understanding and preparation.
How can NCERT Solutions for Class 12 Chemistry Chapter 1 benefit students?
These solutions provide comprehensive explanations and help students clarify their doubts. They serve as a valuable resource for self-study, revision, and exam preparation, enabling students to achieve better academic performance.
Why is understanding the solid state important in chemistry?
The solid state is crucial in chemistry as it forms the basis for understanding various properties and behaviors of solid materials, including metals, ceramics, and polymers. It helps explain phenomena like conductivity, magnetism, and mechanical properties observed in solids.
What are the types of questions I can expect from Chapter 1 "The Solid State"?
Questions in this chapter may include definitions, explanations of concepts, numerical problems related to calculating density, void space, and packing efficiency, as well as questions on the properties of different types of solids.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.