
NCERT Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics
NCERT Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics is prepared by our senior and renowned teachers of Physics Wallah primary focus while solving these questions of class-12 in NCERT textbook, also do read theory of this Chapter 4 Chemical Kinetics while going before solving NCERT questions. Our Physics Wallah team Prepared Other Subjects NCERT Solutions for class 12.NCERT Solutions for Class 12 Chemistry Chapter 1
NCERT Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics Overview
NCERT Solutions for Class 12 Chemistry Chapter 4 cover several important topics. It is highly recommended for students to review each topic thoroughly in order to gain a comprehensive understanding of the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the result of dedicated efforts by the Physics Wallah teachers aimed at assisting students in grasping the concepts covered in this chapter. By going through and practicing these solutions, the objective is for students to achieve excellent results in their exams effortlessly.NCERT Solutions for Class 12 Chemistry Chapter 4
Answer the following Questions of NCERT Solutions for Class 12 Chemistry Chapter 4:
Question 1. For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds. Solution : Average rate of reaction
 = 6.67 × 10
−6 M s−1
Question
2. In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L
−1
to 0.4 mol L
−1
in 10 minutes. Calculate the rate during this interval?
Solution :
= 6.67 × 10
−6 M s−1
Question
2. In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L
−1
to 0.4 mol L
−1
in 10 minutes. Calculate the rate during this interval?
Solution :
 = 0.005 mol L
−1 min−1
= 5 × 10
−3
M min
−1
Question
3. For a reaction, A + B → Product; the rate law is given by, r = k [A]
½
[B]
2
. What is the order of the reaction?
Solution :
The order of the reaction r = k [A]
½
[B]
2
= 1 / 2 + 2
= 2.5
= 0.005 mol L
−1 min−1
= 5 × 10
−3
M min
−1
Question
3. For a reaction, A + B → Product; the rate law is given by, r = k [A]
½
[B]
2
. What is the order of the reaction?
Solution :
The order of the reaction r = k [A]
½
[B]
2
= 1 / 2 + 2
= 2.5
NCERT Solutions for Class 12 Chemistry Chapter 2
Question 4. The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y? Solution : The reaction X → Y follows second order kinetics. Therefore, the rate equation for this reaction will be: Rate = k[X] 2 (1) Let [X] = a mol L −1 , then equation (1) can be written as: Rate 1 = k .(a) 2 = ka 2 If the concentration of X is increased to three times, then [X] = 3a mol L −1 Now, the rate equation will be: Rate = k (3a) 2 = 9(ka 2) Hence, the rate of formation will increase by 9 times.NCERT Solutions for Class 12 Chemistry Chapter 3
Question 5. A first order reaction has a rate constant 1.15 10 −3 s −1 . How long will 5 g of this reactant take to reduce to 3 g? Solution : From the question, we can write down the following information: Initial amount = 5 g Final concentration = 3 g Rate constant = 1.15 10 −3 s −1 We know that for a 1 st order reaction, = 444.38 s
= 444 s (approx)
= 444.38 s
= 444 s (approx)
NCERT Solutions for Class 12 Chemistry Chapter 4
Question 6. Time required to decompose SO 2 Cl 2 to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction. Solution : We know that for a 1 st order reaction, t ½ = 0.693 / k It is given that t 1/2 = 60 min k = 0.693 / t½ = 0.693 / 60 = 0.01155 min -1 = 1.155 min -1 Or k = 1.925 x 10-2 s -1NCERT Solutions for Class 12 Chemistry Chapter 5
Question 7. What will be the effect of temperature on rate constant? Solution : The rate constant of a reaction is nearly doubled with a 10° rise in temperature. However, the exact dependence of the rate of a chemical reaction on temperature is given by Arrhenius equation, k = Ae - E a / RT Where, A is the Arrhenius factor or the frequency factor T is the temperature R is the gas constant E a is the activation energy Question 8. The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate E a . Solution : It is given that T 1 = 298 K ∴T 2 = (298 + 10) K = 308 K We also know that the rate of the reaction doubles when temperature is increased by 10°. Therefore, let us take the value of k 1 = k and that of k 2 = 2k Also, R = 8.314 J K −1 mol−1 Now, substituting these values in the equation: = 52897.78 J mol
−1
= 52.9 kJ mol
−1
Question
9. The activation energy for the reaction 2HI
(
g
)
→ H
2
+ I
2(
g
)
is 209.5 kJ mol
−1
at 581K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Solution :
In the given case:
E
a
= 209.5 kJ mol
−1
= 209500 J mo
l−1
T = 581 K
R = 8.314 JK
−1
mol
−1
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as:
x = e
−Ea / RT
⇒Inx= −Ea / RT
⇒logx=−Ea / 2.303RT
⇒logx= −209500Jmol
−1
/ 2.303 × 8.314JK
−1
mol
−1
×581
=−18.8323
Now,x= Antilog (−18.8323)
=1.471×10
−19
Question
10. From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3 NO(g) → N
2
O
(g) Rate = k[NO]
2
(ii) H
2
O
2
(aq) + 3 I
−
(aq)
+ 2 H
+
→ 2 H
2
O (l) + I
3
-
Rate = k[H
2
O
2
][I
−
]
(iii) CH
3
CHO(g) → CH
4
(g) + CO(g) Rate = k [CH
3
CHO]
3/2
(iv) C
2
H
5
Cl(g) → C
2
H
4
(g) + HCl(g) Rate = k [C
2
H
5
Cl]
Solution :
(i) Given rate = k [NO]
2
Therefore, order of the reaction = 2
Dimension of k = Rate / [NO]
2
= mol L
-1
s
-1
/ (mol L-1)
2
= mol L
-1
s
-1
/ mol
2
L
-2
= L mol
-1
s
-1
(ii) Given rate = k [H
2
O
2
] [I
−
]
Therefore, order of the reaction = 2
Dimension of
k = Rate / [H
2
O
2
][I
-
]
= mol L
-1
s
-1
/ (mol L
-1
) (mol L
-1
)
= L mol
-1
s
-1
(iii) Given rate = k [CH
3
CHO]
3/2
Therefore, order of reaction = 3 / 2
Dimension of k = Rate / [CH3CHO]
3/2
= mol L
-1
s
-1
/ (mol L
-1
)
3/2
= mol L
-1
s
-1
/ mol
3/2
L
-3/2
= L½ mol-½ s-1
(iv) Given rate = k [C
2
H
5
Cl]
Therefore, order of the reaction = 1
Dimension of k = Rate / [C
2
H
5
Cl]
= mol L
-1
s
-1
/ mol L
-1
= s
-1
Question
11. For the reaction:
2A + B → A
2
B
the rate = k[A][B]
2
with k = 2.0 × 10
−6
mol
−2
L
2
s
−1
. Calculate the initial rate of the reaction when [A] = 0.1 mol L−1, [B] = 0.2 mol L
−1
. Calculate the rate of reaction after [A] is reduced to 0.06 mol L
−1
.
Solution :
The initial rate of the reaction is
Rate = k [A][B]
2
= (2.0 × 10
−6 mol−2
L
2
s
−1
) (0.1 mol L
−1
) (0.2 mol L
−1
)
2
= 8.0 × 10
−9
mol
−2
L
2
s
−1
When [A] is reduced from 0.1 mol L
−1
to 0.06 mol
−1
, the concentration of A reacted = (0.1 − 0.06) mol L
−1
= 0.04 mol L
−1
Therefore, concentration of B reacted 1/2 x 0.04 mol L
-1
= 0.02 mol L
−1
Then, concentration of B available, [B] = (0.2 − 0.02) mol L
−1
= 0.18 mol L
−1
After [A] is reduced to 0.06 mol L
−1
, the rate of the reaction is given by,
Rate = k [A][B]
2
= (2.0 × 10
−6
mol
−2
L
2
s
−1
) (0.06 mol L
−1
) (0.18 mol L
−1
)
2
= 3.89 mol L
−1
s
−1
Question
12. The decomposition of NH
3
on platinum surface is zero order reaction. What are the rates of production of N
2
and H
2
if k = 2.5 × 10
−4
mol
−1
L s
−1
?
Solution :
The decomposition of NH
3
on platinum surface is represented by the following equation.
= 52897.78 J mol
−1
= 52.9 kJ mol
−1
Question
9. The activation energy for the reaction 2HI
(
g
)
→ H
2
+ I
2(
g
)
is 209.5 kJ mol
−1
at 581K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Solution :
In the given case:
E
a
= 209.5 kJ mol
−1
= 209500 J mo
l−1
T = 581 K
R = 8.314 JK
−1
mol
−1
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as:
x = e
−Ea / RT
⇒Inx= −Ea / RT
⇒logx=−Ea / 2.303RT
⇒logx= −209500Jmol
−1
/ 2.303 × 8.314JK
−1
mol
−1
×581
=−18.8323
Now,x= Antilog (−18.8323)
=1.471×10
−19
Question
10. From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3 NO(g) → N
2
O
(g) Rate = k[NO]
2
(ii) H
2
O
2
(aq) + 3 I
−
(aq)
+ 2 H
+
→ 2 H
2
O (l) + I
3
-
Rate = k[H
2
O
2
][I
−
]
(iii) CH
3
CHO(g) → CH
4
(g) + CO(g) Rate = k [CH
3
CHO]
3/2
(iv) C
2
H
5
Cl(g) → C
2
H
4
(g) + HCl(g) Rate = k [C
2
H
5
Cl]
Solution :
(i) Given rate = k [NO]
2
Therefore, order of the reaction = 2
Dimension of k = Rate / [NO]
2
= mol L
-1
s
-1
/ (mol L-1)
2
= mol L
-1
s
-1
/ mol
2
L
-2
= L mol
-1
s
-1
(ii) Given rate = k [H
2
O
2
] [I
−
]
Therefore, order of the reaction = 2
Dimension of
k = Rate / [H
2
O
2
][I
-
]
= mol L
-1
s
-1
/ (mol L
-1
) (mol L
-1
)
= L mol
-1
s
-1
(iii) Given rate = k [CH
3
CHO]
3/2
Therefore, order of reaction = 3 / 2
Dimension of k = Rate / [CH3CHO]
3/2
= mol L
-1
s
-1
/ (mol L
-1
)
3/2
= mol L
-1
s
-1
/ mol
3/2
L
-3/2
= L½ mol-½ s-1
(iv) Given rate = k [C
2
H
5
Cl]
Therefore, order of the reaction = 1
Dimension of k = Rate / [C
2
H
5
Cl]
= mol L
-1
s
-1
/ mol L
-1
= s
-1
Question
11. For the reaction:
2A + B → A
2
B
the rate = k[A][B]
2
with k = 2.0 × 10
−6
mol
−2
L
2
s
−1
. Calculate the initial rate of the reaction when [A] = 0.1 mol L−1, [B] = 0.2 mol L
−1
. Calculate the rate of reaction after [A] is reduced to 0.06 mol L
−1
.
Solution :
The initial rate of the reaction is
Rate = k [A][B]
2
= (2.0 × 10
−6 mol−2
L
2
s
−1
) (0.1 mol L
−1
) (0.2 mol L
−1
)
2
= 8.0 × 10
−9
mol
−2
L
2
s
−1
When [A] is reduced from 0.1 mol L
−1
to 0.06 mol
−1
, the concentration of A reacted = (0.1 − 0.06) mol L
−1
= 0.04 mol L
−1
Therefore, concentration of B reacted 1/2 x 0.04 mol L
-1
= 0.02 mol L
−1
Then, concentration of B available, [B] = (0.2 − 0.02) mol L
−1
= 0.18 mol L
−1
After [A] is reduced to 0.06 mol L
−1
, the rate of the reaction is given by,
Rate = k [A][B]
2
= (2.0 × 10
−6
mol
−2
L
2
s
−1
) (0.06 mol L
−1
) (0.18 mol L
−1
)
2
= 3.89 mol L
−1
s
−1
Question
12. The decomposition of NH
3
on platinum surface is zero order reaction. What are the rates of production of N
2
and H
2
if k = 2.5 × 10
−4
mol
−1
L s
−1
?
Solution :
The decomposition of NH
3
on platinum surface is represented by the following equation.
 = 7.5 × 10
−4
mol L
−1
s
−1
Question
13. The decomposition of dimethyl ether leads to the formation of CH
4
, H
2
and CO and the reaction rate is given by
Rate = k [CH
3
OCH
3
]
3/2
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
rate = k (P
CH3OCH3
)
3/2
If the pressure is measured in bar andtime in minutes, then what are the units of rate and rate constants?
Solution :
If pressure is measured in bar and time in minutes, then
Unit of rate = bar min
−1
Rate = k [CH
3
OCH
3
]
3/2
⇒ k =
Rate / [CH
3
OCH
3
]
3/2
Therefore, unit of rate constants(k) = bar min
−1 /
bar
3/2
= bar
-½
min
-1
Question
14. Mention the factors that affect the rate of a chemical reaction.
Solution :
The factors that affect the rate of a reaction are as follows.
(i) Concentration of reactants (pressure in case of gases)
(ii) Temperature
(iii) Presence of a catalyst
Question 15. A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is
(i) doubled (ii) reduced to half?
Solution :
Letthe concentration of the reactant be [A] = a
Rate of reaction, R = k [A]
2
= ka
2
(i)If the concentration of the reactant is doubled, i.e. [A] = 2a, then the rate of the reaction would be
R = k(2a)
2
= 4ka
2
= 4 R
Therefore, the rate of the reaction would increase by 4 times.
(ii) If the concentration of the reactant is reduced to half, i.e. [A] = 1/2 a , then the rate of the reaction would be
R = k(1/2a)
2
= 1/4 Ka
2
= 1/4 R
Therefore, the rate of the reaction would be reduced to
Question 16. What change would happen in the rate constant of a reaction when there is a change in its temperature? How can this temperature effect on rate constant be represented quantitatively?
Solution :
When a temperature of 10∘ rises for a chemical reaction then the rate constant increases and becomes near to double of its original value.
The temperature effect on the rate constant can be represented quantitatively by Arrhenius equation,
k=Ae
−Ea/RT
Where,
k = rate constant,
A = Frequency factor / Arrhenius factor,
R = gas constant
T = temperature
Ea = activation energy for the reaction.
Question
17. In a pseudo first order hydrolysis of ester in water, the following results were obtained:
= 7.5 × 10
−4
mol L
−1
s
−1
Question
13. The decomposition of dimethyl ether leads to the formation of CH
4
, H
2
and CO and the reaction rate is given by
Rate = k [CH
3
OCH
3
]
3/2
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
rate = k (P
CH3OCH3
)
3/2
If the pressure is measured in bar andtime in minutes, then what are the units of rate and rate constants?
Solution :
If pressure is measured in bar and time in minutes, then
Unit of rate = bar min
−1
Rate = k [CH
3
OCH
3
]
3/2
⇒ k =
Rate / [CH
3
OCH
3
]
3/2
Therefore, unit of rate constants(k) = bar min
−1 /
bar
3/2
= bar
-½
min
-1
Question
14. Mention the factors that affect the rate of a chemical reaction.
Solution :
The factors that affect the rate of a reaction are as follows.
(i) Concentration of reactants (pressure in case of gases)
(ii) Temperature
(iii) Presence of a catalyst
Question 15. A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is
(i) doubled (ii) reduced to half?
Solution :
Letthe concentration of the reactant be [A] = a
Rate of reaction, R = k [A]
2
= ka
2
(i)If the concentration of the reactant is doubled, i.e. [A] = 2a, then the rate of the reaction would be
R = k(2a)
2
= 4ka
2
= 4 R
Therefore, the rate of the reaction would increase by 4 times.
(ii) If the concentration of the reactant is reduced to half, i.e. [A] = 1/2 a , then the rate of the reaction would be
R = k(1/2a)
2
= 1/4 Ka
2
= 1/4 R
Therefore, the rate of the reaction would be reduced to
Question 16. What change would happen in the rate constant of a reaction when there is a change in its temperature? How can this temperature effect on rate constant be represented quantitatively?
Solution :
When a temperature of 10∘ rises for a chemical reaction then the rate constant increases and becomes near to double of its original value.
The temperature effect on the rate constant can be represented quantitatively by Arrhenius equation,
k=Ae
−Ea/RT
Where,
k = rate constant,
A = Frequency factor / Arrhenius factor,
R = gas constant
T = temperature
Ea = activation energy for the reaction.
Question
17. In a pseudo first order hydrolysis of ester in water, the following results were obtained:
| t/s | 0 | 30 | 60 | 90 |
| [Ester]mol L −1 | 0.55 | 0.31 | 0.17 | 0.085 |
 Question
19. In a reaction between A and B, the initial rate of reaction (r
0
) was measured for different initial concentrations of A and B as given below:
Question
19. In a reaction between A and B, the initial rate of reaction (r
0
) was measured for different initial concentrations of A and B as given below:
| A/ mol L −1 | 0.20 | 0.20 | 0.40 |
| B/ mol L −1 | 0.30 | 0.10 | 0.05 |
| r 0 / mol L −1 s −1 | 5.07 × 10 −5 | 5.07 × 10 −5 | 1.43 × 10 −4 |
 Dividing equation (iii) by (ii), we obtain
= 1.496
= 1.5 (approximately)
Hence, the order of the reaction with respect to A is 1.5 and with respect to B is zero.
Question
20. The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D
Dividing equation (iii) by (ii), we obtain
= 1.496
= 1.5 (approximately)
Hence, the order of the reaction with respect to A is 1.5 and with respect to B is zero.
Question
20. The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D
| Experiment | A/ mol L −1 | B/ mol L −1 | Initial rate of formation of D/mol L −1 min−1 |
| I | 0.1 | 0.1 | 6.0 × 10 −3 |
| II | 0.3 | 0.2 | 7.2 × 10 −2 |
| III | 0.3 | 0.4 | 2.88 × 10 −1 |
| IV | 0.4 | 0.1 | 2.40 × 10 −2 |
 Dividing equation (iv) by (i), we obtain
Dividing equation (iv) by (i), we obtain
 Dividing equation (iii) by (ii), we obtain
Dividing equation (iii) by (ii), we obtain

 Question
21. The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
Question
21. The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
| Experiment | A/ mol L −1 | B/ mol L −1 | Initial rate/mol L −1 min −1 |
| I | 0.1 | 0.1 | 2.0 × 10 −2 |
| II | -- | 0.2 | 4.0 × 10 −2 |
| III | 0.4 | 0.4 | -- |
| IV | -- | 0.2 | 2.0 × 10 −2 |
 = 1845 years (approximately)
Hence, the age of the sample is 1845 years.
Question
24. The experimental data for decomposition of N
2
O
5
[2N2O5 → 4NO2 + O2] in gas phase at 318K are given below:
= 1845 years (approximately)
Hence, the age of the sample is 1845 years.
Question
24. The experimental data for decomposition of N
2
O
5
[2N2O5 → 4NO2 + O2] in gas phase at 318K are given below:
| t(s) | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| 10 2 × [N 2 O 5 ] mol L -1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
 (ii) Time corresponding to the concentration, 1630x10
2
/ 2 mol L
-1
= 81.5 mol L
-1
is the half life. From the graph, the half life is obtained as 1450 s.
(iii)
(ii) Time corresponding to the concentration, 1630x10
2
/ 2 mol L
-1
= 81.5 mol L
-1
is the half life. From the graph, the half life is obtained as 1450 s.
(iii)
| t(s) | 10 2 × [N 2 O 5 ] mol L -1 | Log[N 2 O 5 ] |
| 0 | 1.63 | − 1.79 |
| 400 | 1.36 | − 1.87 |
| 800 | 1.14 | − 1.94 |
| 1200 | 0.93 | − 2.03 |
| 1600 | 0.78 | − 2.11 |
| 2000 | 0.64 | − 2.19 |
| 2400 | 0.53 | − 2.28 |
| 2800 | 0.43 | − 2.37 |
| 3200 | 0.35 | − 2.46 |
 (iv) The given reaction is of the first order as the plot, Log[N
2
O
5
] v/s t, is a straight line. Therefore, the rate law of the reaction is
Rate = k [N
2
O
5
]
(v) From the plot, Log[N
2
O
5
] v/s t, we obtain
- k /2.303
Again, slope of the line of the plot Log[N
2
O
5
] v/s t is given by
- k / 2.303. = -0.67 / 3200
Therefore, we obtain,
- k / 2.303 = - 0.67 / 3200
⇒ k = 4.82 x 10-4 s-1
(vi) Half-life is given by,
t
½
= 0.693 / k
= 0.639 / 4.82x10
-4
s
=1.438 x 103
This value, 1438 s, is very close to the value that was obtained from the graph.
Question 25. The rate constant for a first order reaction is 60 s
−1
. How much time will it take to reduce the initial concentration of the reactant to its 1/16
th
value?
Solution :
It is known that,
(iv) The given reaction is of the first order as the plot, Log[N
2
O
5
] v/s t, is a straight line. Therefore, the rate law of the reaction is
Rate = k [N
2
O
5
]
(v) From the plot, Log[N
2
O
5
] v/s t, we obtain
- k /2.303
Again, slope of the line of the plot Log[N
2
O
5
] v/s t is given by
- k / 2.303. = -0.67 / 3200
Therefore, we obtain,
- k / 2.303 = - 0.67 / 3200
⇒ k = 4.82 x 10-4 s-1
(vi) Half-life is given by,
t
½
= 0.693 / k
= 0.639 / 4.82x10
-4
s
=1.438 x 103
This value, 1438 s, is very close to the value that was obtained from the graph.
Question 25. The rate constant for a first order reaction is 60 s
−1
. How much time will it take to reduce the initial concentration of the reactant to its 1/16
th
value?
Solution :
It is known that,
 Question
26. During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If 1μg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
Solution :
Question
26. During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If 1μg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
Solution :
 Therefore, 0.7814 μg of 90
Sr
will remain after 10 years.
Again,
Therefore, 0.7814 μg of 90
Sr
will remain after 10 years.
Again,
 Therefore, 0.2278 μg of 90
Sr
will remain after 60 years.
Question
27. For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
Solution :
For a first order reaction, the time required for 99% completion is
t
1
= 2.303/k Log 100/100-99
= 2.303/k Log 100
= 2x 2.303/k
For a first order reaction, the time required for 90% completion is
t
2
= 2.303/k Log 100 / 100-90
= 2.303/k Log 10
= 2.303/k
Therefore, t
1
= 2t
2
Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.
Question
28. A first order reaction takes 40 min for 30% decomposition. Calculate t
1/2
.
Solution :
For a first order reaction,
t = 2.303/k Log [R] º / [R]
k = 2.303/40min Log 100 / 100-30
= 2.303/40min Log 10 / 7
= 8.918 x 10-3 min
-1
Therefore, t
1/2
of the decomposition reaction is
t1/2 = 0.693/k
= 0.693 / 8.918 x 10-3 min
= 77.7 min (approximately)
= 77.7 min (approximately)
Question
29. For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
Therefore, 0.2278 μg of 90
Sr
will remain after 60 years.
Question
27. For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
Solution :
For a first order reaction, the time required for 99% completion is
t
1
= 2.303/k Log 100/100-99
= 2.303/k Log 100
= 2x 2.303/k
For a first order reaction, the time required for 90% completion is
t
2
= 2.303/k Log 100 / 100-90
= 2.303/k Log 10
= 2.303/k
Therefore, t
1
= 2t
2
Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.
Question
28. A first order reaction takes 40 min for 30% decomposition. Calculate t
1/2
.
Solution :
For a first order reaction,
t = 2.303/k Log [R] º / [R]
k = 2.303/40min Log 100 / 100-30
= 2.303/40min Log 10 / 7
= 8.918 x 10-3 min
-1
Therefore, t
1/2
of the decomposition reaction is
t1/2 = 0.693/k
= 0.693 / 8.918 x 10-3 min
= 77.7 min (approximately)
= 77.7 min (approximately)
Question
29. For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
| t (sec) | P(mm of Hg) |
| 0 | 35.0 |
| 360 | 54.0 |
| 720 | 63.0 |
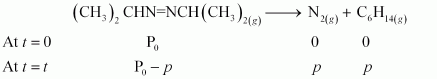 After time, t, total pressure, Pt = (P
º
- p) + p + p
⇒ Pt = (P
º
+ p)
⇒ p = P
t
- P
0
therefore, P
º
- p = P
0
- Pt - P
0
= 2P
0
− P
t
For a first order reaction,
k = 2.303/t Log P
0
/P
0
- p
= 2.303/t Log P
0
/ 2 P
0
- P
t
When t = 360 s, k = 2.303 / 360s log 35.0 / 2x35.0 - 54.0
= 2.175 × 10
−3
s
−1
When t = 720 s, k = 2.303 / 720s log 35.0 / 2x35.0 - 63.0
= 2.235 × 10
−3
s
−1
Hence, the average value of rate constant is
k = (2.175 × 10
- 3
+ 2.235 × 10
- 3
) / 2 s
- 1
= 2.21 × 10
−3
s
−1
Question
30. The following data were obtained during the first order thermal decomposition of SO
2
Cl
2
at a constant volume.
SO
2
Cl
2
(g) → SO
2
(g) + Cl
2
(g)
After time, t, total pressure, Pt = (P
º
- p) + p + p
⇒ Pt = (P
º
+ p)
⇒ p = P
t
- P
0
therefore, P
º
- p = P
0
- Pt - P
0
= 2P
0
− P
t
For a first order reaction,
k = 2.303/t Log P
0
/P
0
- p
= 2.303/t Log P
0
/ 2 P
0
- P
t
When t = 360 s, k = 2.303 / 360s log 35.0 / 2x35.0 - 54.0
= 2.175 × 10
−3
s
−1
When t = 720 s, k = 2.303 / 720s log 35.0 / 2x35.0 - 63.0
= 2.235 × 10
−3
s
−1
Hence, the average value of rate constant is
k = (2.175 × 10
- 3
+ 2.235 × 10
- 3
) / 2 s
- 1
= 2.21 × 10
−3
s
−1
Question
30. The following data were obtained during the first order thermal decomposition of SO
2
Cl
2
at a constant volume.
SO
2
Cl
2
(g) → SO
2
(g) + Cl
2
(g)
| Experiment | Time/s −1 | Total pressure/atm |
| 1 | 0 | 0.5 |
| 2 | 100 | 0.6 |
 After time, t, total pressure, P
t
= (P
º
- p) + p + p
⇒ P
t
= (P
º
+ p)
⇒ p = Pt - Pº
therefore, Pº - p = Pº - Pt - Pº
= 2 P
º
- P
t
For a first order reaction,
k = 2.303/t Log P
º
/ P
º
- p
= 2.303/t Log P
º
/ 2 P
º
- Pt
When t= 100 s,
k = 2.303 / 100s log 0.5 / 2x0.5 - 0.6
= 2.231 × 10 - 3s - 1
When Pt= 0.65 atm,
P0+ p= 0.65
⇒ p= 0.65 - P0
= 0.65 - 0.5
= 0.15 atm
Therefore, when the total pressure is 0.65 atm, pressure of SOCl2 is
PSOCL2
= P
0
- p
= 0.5 - 0.15
= 0.35 atm
Therefore, the rate of equation, when total pressure is 0.65 atm, is given by,
Rate = k(p
SOCL2
)
= (2.23 × 10 - 3s - 1) (0.35 atm)
= 7.8 × 10
- 4
atm s
- 1
Question
31. The rate constant for the decomposition of N
2
O
5
at various temperatures is given below:
After time, t, total pressure, P
t
= (P
º
- p) + p + p
⇒ P
t
= (P
º
+ p)
⇒ p = Pt - Pº
therefore, Pº - p = Pº - Pt - Pº
= 2 P
º
- P
t
For a first order reaction,
k = 2.303/t Log P
º
/ P
º
- p
= 2.303/t Log P
º
/ 2 P
º
- Pt
When t= 100 s,
k = 2.303 / 100s log 0.5 / 2x0.5 - 0.6
= 2.231 × 10 - 3s - 1
When Pt= 0.65 atm,
P0+ p= 0.65
⇒ p= 0.65 - P0
= 0.65 - 0.5
= 0.15 atm
Therefore, when the total pressure is 0.65 atm, pressure of SOCl2 is
PSOCL2
= P
0
- p
= 0.5 - 0.15
= 0.35 atm
Therefore, the rate of equation, when total pressure is 0.65 atm, is given by,
Rate = k(p
SOCL2
)
= (2.23 × 10 - 3s - 1) (0.35 atm)
= 7.8 × 10
- 4
atm s
- 1
Question
31. The rate constant for the decomposition of N
2
O
5
at various temperatures is given below:
| T/°C | 0 | 20 | 40 | 60 | 80 |
| 10 5 X K /S -1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
| T/°C | 0 | 20 | 40 | 60 | 80 |
| T/K | 273 | 293 | 313 | 333 | 353 |
| 1/T / k -1 | 3.66×10 −3 | 3.41×10 −3 | 3.19×10 −3 | 3.0×10 −3 | 2.83 ×10 −3 |
| 10 5 X K /S -1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
| ln k | −7.147 | − 4.075 | −1.359 | −0.577 | 3.063 |
 Slope of the line,
Slope of the line,
 In k= - 2.8
Therefore, k = 6.08x10-2s-1
Again when T = 50 + 273K = 323K,
1/T = 3.1 x 10-3 K
In k = - 0.5
Therefore, k = 0.607 s-1
Question
32. The rate constant for the decomposition of hydrocarbons is 2.418 × 10
−5
s
−1
at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor.
Solution :
k = 2.418 × 10
−5
s
−1
T = 546 K
E
a
= 179.9 kJ mol
−1
= 179.9 × 10
3
J mol
−1
According to the Arrhenius equation,
In k= - 2.8
Therefore, k = 6.08x10-2s-1
Again when T = 50 + 273K = 323K,
1/T = 3.1 x 10-3 K
In k = - 0.5
Therefore, k = 0.607 s-1
Question
32. The rate constant for the decomposition of hydrocarbons is 2.418 × 10
−5
s
−1
at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor.
Solution :
k = 2.418 × 10
−5
s
−1
T = 546 K
E
a
= 179.9 kJ mol
−1
= 179.9 × 10
3
J mol
−1
According to the Arrhenius equation,
 = (0.3835 − 5) + 17.2082
= 12.5917
Therefore, A = antilog (12.5917)
= 3.9 × 10
12
s
−1
(approximately)
Question
33. Consider a certain reaction A → Products with k = 2.0 × 10
−2
s
−1
. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L
−1
.
Solution :
k = 2.0 × 10
−2
s
−1
T = 100 s
[A]
o
= 1.0 moL
−1
Since the unit of k is s
−1
, the given reaction is a first order reaction.
Therefore, k = 2.303/t Log [A]º / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s Log 1.0 / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s ( - Log [A] )
⇒ - Log [A] = - (2.0 x 10-2 x 100) / 2.303
⇒ [A] = antilog [- (2.0 x 10-2 x 100) / 2.303]
= 0.135 mol L
−1 (approximately)
Hence, the remaining concentration of A is 0.135 mol L
−1.
Question
34. Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t
1/2
= 3.00 hours. What fraction of sample of sucrose remains after 8 hours?
Solution :
For a first order reaction,
k = 2.303/t Log [R]º / [R]
It is given that, t1/2 = 3.00 hours
Therefore, k = 0.693 / t1/2
= 0.693 / 3 h-1
= 0.231 h - 1
Then, 0.231 h - 1 = 2.303 / 8h Log [R]º / [R]
= (0.3835 − 5) + 17.2082
= 12.5917
Therefore, A = antilog (12.5917)
= 3.9 × 10
12
s
−1
(approximately)
Question
33. Consider a certain reaction A → Products with k = 2.0 × 10
−2
s
−1
. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L
−1
.
Solution :
k = 2.0 × 10
−2
s
−1
T = 100 s
[A]
o
= 1.0 moL
−1
Since the unit of k is s
−1
, the given reaction is a first order reaction.
Therefore, k = 2.303/t Log [A]º / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s Log 1.0 / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s ( - Log [A] )
⇒ - Log [A] = - (2.0 x 10-2 x 100) / 2.303
⇒ [A] = antilog [- (2.0 x 10-2 x 100) / 2.303]
= 0.135 mol L
−1 (approximately)
Hence, the remaining concentration of A is 0.135 mol L
−1.
Question
34. Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t
1/2
= 3.00 hours. What fraction of sample of sucrose remains after 8 hours?
Solution :
For a first order reaction,
k = 2.303/t Log [R]º / [R]
It is given that, t1/2 = 3.00 hours
Therefore, k = 0.693 / t1/2
= 0.693 / 3 h-1
= 0.231 h - 1
Then, 0.231 h - 1 = 2.303 / 8h Log [R]º / [R]
 Hence, the fraction of sample of sucrose that remains after 8 hours is 0.158.
Question
35. The decomposition of hydrocarbon follows the equation k = (4.5 × 10
11
s
−1
) e
−28000
K/T Calculate E
a
.
Solution :
The given equation is
k = (4.5 × 10
11
s
−1
) e
−28000
K/T (i)
Arrhenius equation is given by,
k= Ae
-Ea/RT
(ii)
From equation (i) and (ii), we obtain
Ea / RT = 28000K / T
⇒ Ea = R x 28000K
= 8.314 J K
−1
mol
−1
× 28000 K
= 232792 J mol
−1
= 232.792 kJ mol
−1
Question
36. The rate constant for the first order decomposition of H
2
O
2
is given by the following equation:
log k = 14.34 − 1.25 × 10
4 K/T
Calculate E
a
for this reaction and at what temperature will its half-period be 256 minutes?
Solution :
Arrhenius equation is given by,
k= Ae -Ea/RT
⇒In k = In A - Ea/RT
⇒In k = Log A - Ea/RT
⇒ Log k = Log A - Ea/2.303RT (i)
The given equation is
Log k = 14.34 - 1.25 104 K/T (ii)
From equation (i) and (ii), we obtain
Ea/2.303RT = 1.25 104 K/T
= 1.25 × 10
4
K × 2.303 × 8.314 J K
−1
mol
−1
= 239339.3 J mol
−1
(approximately)
= 239.34 kJ mol
−1
Also, when t
1/2
= 256 minutes,
k = 0.693 / t
1/2
= 0.693 / 256
= 2.707 × 10
- 3
min
- 1
= 4.51 × 10 - 5s
- 1
= 2.707 × 10
−3
min
−1
= 4.51 × 10
−5
s
−1
It is also given that, log k = 14.34 − 1.25 × 10
4
K/T
Hence, the fraction of sample of sucrose that remains after 8 hours is 0.158.
Question
35. The decomposition of hydrocarbon follows the equation k = (4.5 × 10
11
s
−1
) e
−28000
K/T Calculate E
a
.
Solution :
The given equation is
k = (4.5 × 10
11
s
−1
) e
−28000
K/T (i)
Arrhenius equation is given by,
k= Ae
-Ea/RT
(ii)
From equation (i) and (ii), we obtain
Ea / RT = 28000K / T
⇒ Ea = R x 28000K
= 8.314 J K
−1
mol
−1
× 28000 K
= 232792 J mol
−1
= 232.792 kJ mol
−1
Question
36. The rate constant for the first order decomposition of H
2
O
2
is given by the following equation:
log k = 14.34 − 1.25 × 10
4 K/T
Calculate E
a
for this reaction and at what temperature will its half-period be 256 minutes?
Solution :
Arrhenius equation is given by,
k= Ae -Ea/RT
⇒In k = In A - Ea/RT
⇒In k = Log A - Ea/RT
⇒ Log k = Log A - Ea/2.303RT (i)
The given equation is
Log k = 14.34 - 1.25 104 K/T (ii)
From equation (i) and (ii), we obtain
Ea/2.303RT = 1.25 104 K/T
= 1.25 × 10
4
K × 2.303 × 8.314 J K
−1
mol
−1
= 239339.3 J mol
−1
(approximately)
= 239.34 kJ mol
−1
Also, when t
1/2
= 256 minutes,
k = 0.693 / t
1/2
= 0.693 / 256
= 2.707 × 10
- 3
min
- 1
= 4.51 × 10 - 5s
- 1
= 2.707 × 10
−3
min
−1
= 4.51 × 10
−5
s
−1
It is also given that, log k = 14.34 − 1.25 × 10
4
K/T
 = 668.95 K
= 669 K (approximately)
Question
37. The decomposition of A into product has value of k as 4.5 × 10
3
s
−1
at 10°C and energy of activation 60 kJ mol
−1
. At what temperature would k be 1.5 × 10
4
s
−1
?
Solution :
From Arrhenius equation, we obtain
log k2/k1 = Ea / 2.303 R (T
2
- T
1
) / T
1
T
2
Also, k
1
= 4.5 × 10
3 s−1
T
1
= 273 + 10 = 283 K
k
2
= 1.5 × 10
4
s
−1
E
a
= 60 kJ mol
−1
= 6.0 × 10
4
J mol
−1
Then,
= 668.95 K
= 669 K (approximately)
Question
37. The decomposition of A into product has value of k as 4.5 × 10
3
s
−1
at 10°C and energy of activation 60 kJ mol
−1
. At what temperature would k be 1.5 × 10
4
s
−1
?
Solution :
From Arrhenius equation, we obtain
log k2/k1 = Ea / 2.303 R (T
2
- T
1
) / T
1
T
2
Also, k
1
= 4.5 × 10
3 s−1
T
1
= 273 + 10 = 283 K
k
2
= 1.5 × 10
4
s
−1
E
a
= 60 kJ mol
−1
= 6.0 × 10
4
J mol
−1
Then,
 = 297 K
= 24°C
Hence, k would be 1.5 × 10
4
s
−1
at 24°C.
Question
38. The time required for 10% completion of a first order reaction at 298 K is equal to that required for its 25% completion at 308 K. If the value of A is 4 × 10
10
s
−1
. Calculate k at 318 K and E
a
.
Solution :
For a first order reaction,
t = 2.303 / k log a / a - x
At 298 K,
t = 2.303
/
k
log
100
/
90
= 0.1054 /
k
At 308 K,
t' = 2.303
/
k'
log
100
/
75
= 2.2877 /
k'
According to the question,
t = t'
⇒
0.1054 /
k =
2.2877 /
k'
⇒ k'
/
k = 2.7296
From Arrhenius equation, we obtain
= 297 K
= 24°C
Hence, k would be 1.5 × 10
4
s
−1
at 24°C.
Question
38. The time required for 10% completion of a first order reaction at 298 K is equal to that required for its 25% completion at 308 K. If the value of A is 4 × 10
10
s
−1
. Calculate k at 318 K and E
a
.
Solution :
For a first order reaction,
t = 2.303 / k log a / a - x
At 298 K,
t = 2.303
/
k
log
100
/
90
= 0.1054 /
k
At 308 K,
t' = 2.303
/
k'
log
100
/
75
= 2.2877 /
k'
According to the question,
t = t'
⇒
0.1054 /
k =
2.2877 /
k'
⇒ k'
/
k = 2.7296
From Arrhenius equation, we obtain
 To calculate k at 318 K,
It is given that, A = 4 x 1010 s-1, T = 318K
Again, from Arrhenius equation, we obtain
To calculate k at 318 K,
It is given that, A = 4 x 1010 s-1, T = 318K
Again, from Arrhenius equation, we obtain
 Therefore, k = Antilog (-1.9855)
= 1.034 x 10-2 s -1
Question
39. The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
Solution :
From Arrhenius equation, we obtain
Therefore, k = Antilog (-1.9855)
= 1.034 x 10-2 s -1
Question
39. The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
Solution :
From Arrhenius equation, we obtain
 Hence, the required energy of activation is 52.86 kJmol
−1.
Hence, the required energy of activation is 52.86 kJmol
−1.
NCERT Solutions for Class 12 Chemistry Chapter 4 FAQs
Why is it important to study Chemical Kinetics in Class 12 Chemistry?
Chemical Kinetics is important as it helps in understanding the speed or rate at which chemical reactions occur. This knowledge is vital for predicting reaction outcomes, optimizing reaction conditions, and designing industrial processes.
How can NCERT Solutions help in understanding Chapter 4 better?
NCERT Solutions provide detailed explanations and step-by-step solutions to the questions and exercises in Chapter 4. They help students understand concepts better, clarify doubts, and prepare effectively for exams.
Are there any practical applications of Chemical Kinetics?
Yes, Chemical Kinetics has numerous practical applications in various fields such as pharmaceuticals, chemical engineering, environmental science, and materials science. It is used to optimize reaction conditions, understand reaction mechanisms, and predict reaction rates in real-world scenarios.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.









