
Binding Energy Formula: The binding energy equation, also known as binding energy, represents the energy equivalent of the mass defect within the nucleus, which comprises protons and neutrons contained within an atom. Protons bear a positive charge, while neutrons are electrically neutral particles. Thus, the atomic nucleus carries a net positive charge. Visually, the nucleus resembles a rigid spherical core encompassing numerous miniature spherical nucleons, akin to tiny balls. To hold these nucleons together, binding particles act as an adhesive, requiring each nucleon to relinquish a portion of its mass, resulting in a mass deficit.
The total binding energy formula defines the energy necessary to disassemble a nucleus into its constituent nucleons. The values obtained from this formula are typically expressed in units such as kJ/mole or MeV/nucleon.
The specific values derived from the binding energy per nucleon formula differ from one atom to another, contingent upon the strength of the nucleus inherent to each atom.
Binding Energy = mass defect * c2
where c represents the speed of light in a vacuum. Which has the constant value.
c = 2.9979 x 108 m/s.
The mass defect formula can be denoted by Δm
Mass defect formula Δm is given below
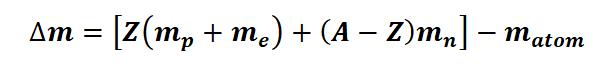
m p represents the mass of a proton (1.007277 amu)
m n represents the mass of a neutron (1.008665 amu)
m e represents the mass of an electron (0.000548597 amu)
m atom denotes the mass of the nuclide
Z represents the atomic number, a fundamental property of the atom.
The binding energy of electrons is alternatively known as the ionization potential of the atom, signifying the energy necessary to dislodge an electron from an atom, molecule, or ion. Notably, the binding energy of an individual neutron or a photon within the nucleus greatly surpasses the binding energy of electrons within an atom. The value derived from the formula for electron binding energy is typically expressed in electronvolts (eV), with 1 eV approx equal to 1.6 x 10−19 joules.
The binding energy of the nucleus formula is used to determine the energy required to break a nucleus into its constituent protons and neutrons. To separate a portion of deuterons into protons and neutrons, approximately two million electronvolts are needed. This formula calculates binding energy by converting mass into energy using Maxwell's equation E = mc2, with mass obtained from the mass defect equation. Mass should be measured in kilograms, and the resultant energy, in joules, is attributed to one nucleus. Joules per nucleus can subsequently be utilized to compute per-nucleon and per-mole quantities.
Binding Energy Formula Solved Examples
Problem 1: Determine the binding energy per nucleon for an alpha particle with a specified mass defect of 0.0382 atomic mass units (amu).
Given: mass defect = 0.0382amu
The mass defect formula for converting to kilograms is as follows:
(Here, 1 amu = 1.6606 x 10 −27 kg)
Mass defect =(0.0382)(1.6606 x 10 −27 )
= 0.0634092 x 10 −27 kg/nucleus
Binding Energy Formula for converting into energy using ΔE = Δmc2
The speed of light, denoted as 'c,' equals 2.9979 x 10 8 meters per second.
Binding Energy Formula: E = (0.0634092 x 10 −27 )(2.9979 x 10 8 ) 2
= 0.5723 x 10 −11 J/nucleus
To convert energy from joules per nucleus to kilojoules per mole
(1 kJ = 1000 J)
For converting the nucleus in to mole by multiplying with the Avogadro number
(6.022 x 10 23 nuclei/mol)
Therefore, E = (0.5723 x 10 −11 )(6.022 x 10 23 )/1000
Binding Energy E = 3.439 x 10 9 kJ/mole
Problem 2 : Determine the binding energy per nucleon for an alpha particle with a specified mass defect of 0.0272 atomic mass units (amu).
Given: mass defect = 0.0272amu
The mass defect formula for converting to kilograms is as follows:
(Here, 1 amu = 1.6606 x 10 −27 kg)
Mass defect =(0.0272)(1.6606 x 10 −27 )
= 0.0452352 x 10 −27 kg/nucleus
Binding Energy Formula for converting into energy using ΔE = Δmc2
The speed of light, denoted as 'c,' equals 2.9979 x 10 8 meters per second.
Binding Energy Formula: E = (0.0452352 x 10 −27 )(2.9979 x 10 8 ) 2
= 0.4064 x 10 −11 J/nucleus
To convert energy from joules per nucleus to kilojoules per mole
(1 kJ = 1000 J)
For converting the nucleus in to mole by multiplying with the Avogadro number (6.022 x 10 23 nuclei/mol)
Therefore, E = (0.4064 x 10 −11 )(6.022 x 10 23 )/1000
Binding Energy E = 2.4485 x 10 9 kJ/mole
Join Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your chemistry knowledge. and build a strong foundation.
| Related Links | |
| Vapor Pressure Formula | Theoretical Yield Formula |
| Arsenic Acid Formula | Strontium Sulfate Formula |
Binding Energy Formula FAQs
What is the Binding Energy Formula?
What is the mass defect in the Binding Energy Formula?
How is mass defect calculated in the Binding Energy Formula?
What are the units of binding energy in the formula?










