Centroid of a Trapezoid Formula - Solved Examples

The formula for calculating the centroid of a trapezoid assists in determining the position of the centroid within a trapezoid, which is a quadrilateral with two parallel sides. The centroid of a trapezoid is located between its two bases. To gain a comprehensive understanding of the centroid of a trapezoid formula, we will explore it further through solved examples.

What is Centroid of a Trapezoid Formula?

The formula to calculate the coordinates of the centroid of a trapezoid is expressed as:

G = (h/2, (b + 2a) / (3(a + b)) * h)

Here, the variables represent:

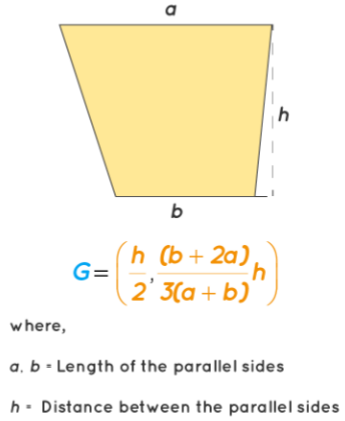
a, b = Length of the parallel sides of the trapezoid

h = Distance between the parallel sides of the trapezoid

This formula allows you to find the coordinates (x, y) of the centroid (G) of a given trapezoid based on its dimensions.

Also Check – Complex number Formula

Examples Using Centroid of a Trapezoid Formula

Example 1: Calculate the centroid of a trapezoid with a height of 6 units and parallel sides measuring 4 units and 8 units.

Solution:

To determine the centroid of the given trapezoid, we will use the centroid of a trapezoid formula:

G = (h/2, (b + 2a) / (3(a + b)) * h)

Given:

h = 6 units

a = 4 units

b = 8 units

Substituting these values into the formula:

G = (6/2, (8 + 2 * 4) / (3 * (4 + 8)) * 6)

G = (3, 2.67)

Answer: The coordinates of the centroid are (3, 2.67), or the centroid is 2.67 units from the side with a length of 8 units.

Also Check – Line and Angles Formula

Example 2: Determine the centroid of a trapezoid with a height of 10 units and parallel sides measuring 5 units and 3 units.

Solution:

To find the centroid of the given trapezoid, we will apply the centroid of a trapezoid formula:

G = (h/2, (b + 2a) / (3(a + b)) * h)

Given:

h = 10 units

a = 3 units

b = 5 units

Using these values in the formula:

G = (10/2, (5 + 2 * 3) / (3 * (3 + 5)) * 10)

G = (5, 4.58)

Answer: The coordinates of the centroid are (5, 4.58), or the centroid is 4.58 units from the side with a length of 5 units.