Work
Work Power And Energy of Class 11
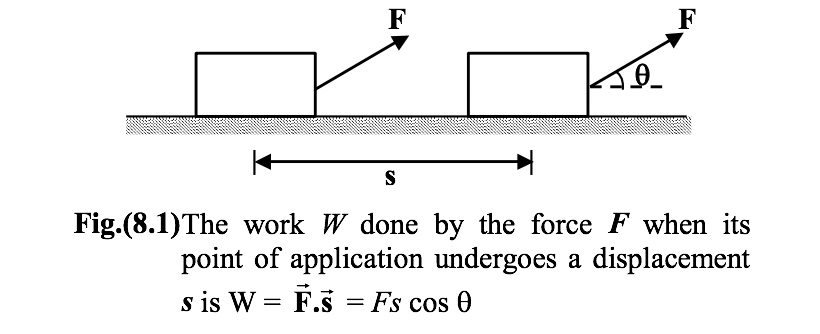
The work W done by a constant force F when its point of application undergoes a displacement s is defined to be
W = F s cos θ (8.1)
where θ is the angle between
![]() and
and
![]() as indicated in figure(8.1). Only the component of
as indicated in figure(8.1). Only the component of
![]() along s, that is , F cosθ , contributes to the work done. Strictly speaking, the work is done by the source or agent that applies the force. Work is a scalar quantity and its SI unit is the joule (J). From equation (8.1), we see that
along s, that is , F cosθ , contributes to the work done. Strictly speaking, the work is done by the source or agent that applies the force. Work is a scalar quantity and its SI unit is the joule (J). From equation (8.1), we see that
1 J = 1 N -m
Work is also defined as the dot product of force and its displacement as given by equation (8.2)
W =
![]() (8.2)
(8.2)
In terms of rectangular components, the two vectors are
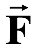 = Fx
= Fx
 + Fy
+ Fy
 + Fz
+ Fz
 and
and
![]() = Δx
= Δx
 + Δy
+ Δy
 + Δz
+ Δz
 ; hence, equation (8.2) may be written as
; hence, equation (8.2) may be written as
W = Fx Δx + Fy Δy + Fz Δz (8.3)
The work done by a given force on a body depends only on the force, the displacement, and the angle between them. It does not depend on the velocity or the acceleration of the body, or on the presence of other forces.
Since the work is a scalar, its value also does not depend on the orientation of the coordinate axes. Since the magnitude of a displacement in a given time interval depends on the velocity of the frame of reference used to measure the displacement, the calculated work also depends on the reference frame.
Example 8.1
A box is moved over a horizontal path by applying force F = 60 N at an angle θ = 30o to the horizontal. What is the work done during the displacement of the box over a distance of 0.5 km.
Solution
By definition, W = F s cos θ
Here F = 60 N; s = 0.5 km = 500 m; θ = 30o.
∴W = (60)(500) cos30o = 26 kJ
Example 8.2
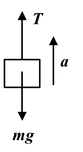
A load of mass m = 3000 kg is lifted by a winch with an acceleration a = 2 m/s2. Find the work done during the first one and a half seconds from the beginning of motion.
Solution
The height to which the body is lifted during the first t second is h = 1/2at 2 .
|
The tension in the rope is given by T = mg + ma Work done is given by W = Th = m(g + a)(1/2at 2) Here m = 3000kg, a = 2m/s 2 ; g = 10m/s 2 ; t = 1.5 s. ∴W = (3000)(10 + 2)[1/2(2)(1.5) 2 ] orW = 81 kJ |
|
Positive and Negative Work
Work done by a force may be positive or negative depending on the angle θ between the force and displacement. If the angle θ is acute (θ < 90o), then the work done is positive and the component of force is parallel to the displacement. (See figure 8.2 a)
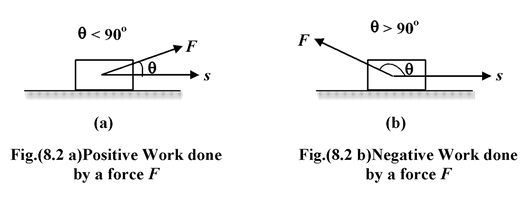
If the angle θ is obtuse (θ > 90 o ), the component of force is antiparallel to the displacement and the work done by force is negative (see fig.(8.2 b))
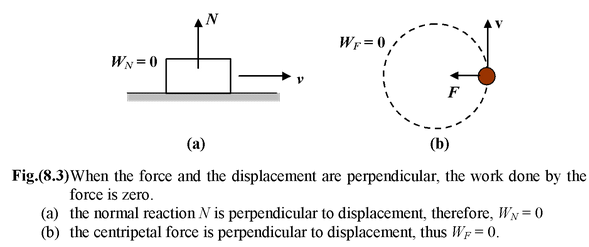
Zero Work Done
It is clear from the equation (8.1) that the work done by a force is zero when
|
(a) F = 0 (b) s = 0 cosθ = 0 or θ = 90o |
|
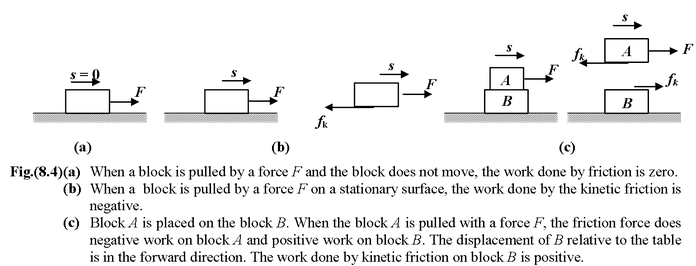
Work Done by Friction
There is a misconception that the force of friction always does negative work. In reality, the work done by friction may be zero, positive or negative depending upon the situation as shown in the figure (8.4).
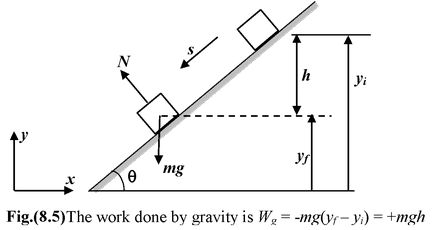
Work Done by Gravity
|
Consider a block of mass m which slides down a smooth inclined plane of angle θ as shown in figure.(8.5). Let us assume the coordinate axes as shown in the figure, to specify the components of the two vectors - although the value of work will not depend on the orientation of the axes. |
|
Now, the force of gravity,
![]() g = -mg
g = -mg
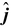
and the displacement is given by
![]() = Δx
= Δx
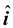 + Δy
+ Δy
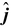 + Δz
+ Δz
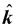
The work done by gravity is
Wg =
![]() g.
g.
![]() = -mg
= -mg
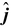 .(Δx
.(Δx
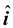 + Δy
+ Δy
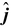 + Δz
+ Δz
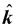 )
)
orWg = -mgΔy(
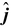 .
.
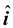 = 0,
= 0,
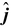 .
.
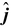 = 1,
= 1,
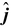 .
.
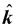 = 0)
= 0)
SinceΔy = yf - yi = −h
∴Wg = −mg(yf - yi) = +mgh
If the block moves in the upward direction, then the work done by gravity is negative and is given by
Wg = −mgh
Important
1.The work done by the force of gravity depends only on the initial and final vertical coordinates, not on the path taken.
2.The work done by gravity is zero for any path that returns to its initial point.
When several forces act on a body one may calculate the work done by each force individually. The net work done on the body is the algebraic sum of individual contributions.
Wnet =
![]() .
.
![]() +
+
![]() .
.
![]() + ………. +
+ ………. +
![]() .
.
![]()
orWnet = W 1 + W 2 + …………… + Wn(8.4)