Cot-Tan Formula: Explanation, Definition and Solved Examples

The Cot-Tan Formula is indeed a trigonometric ratios that describes the relationship between the sides of a right-angled triangle. Specifically:

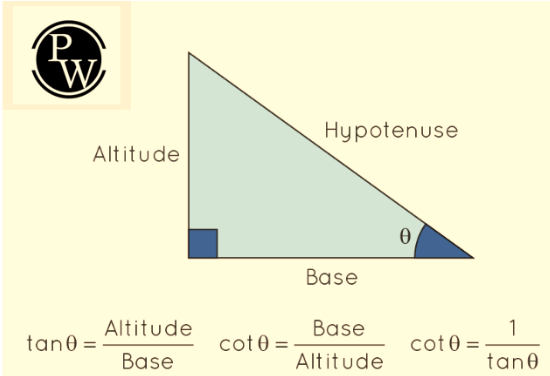
Tanθ (tangent of θ) is the ratio of the length of the side opposite angle θ to the length of the side adjacent to angle θ.

Cotθ (cotangent of θ) is the reciprocal of the tangent, which means Cotθ is the ratio of the length of the side adjacent to angle θ to the length of the side opposite angle θ.

In other words:

Tanθ = (opposite side) / (adjacent side)

Cotθ = (adjacent side) / (opposite side)

As you mentioned, there is an inverse relationship between Cotθ and Tanθ. Specifically, Cotθ is the reciprocal of Tanθ and vice versa. This relationship is expressed as:

Cotθ = 1 / Tanθ

Tanθ = 1 / Cotθ

These trigonometric ratios are fundamental in trigonometry and have applications in various fields, including geometry, physics, engineering, and more. They are used to calculate angles, distances, and heights in various real-world problems.

Relationship Between Cotθ and Tanθ

The cotangent (Cotθ) and tangent (Tanθ) trigonometric ratios are indeed inversely related, and you've correctly expressed this relationship as:

Cotθ = 1 / Tanθ

This means that if you know the tangent of an angle (Tanθ), you can easily find the cotangent (Cotθ) by taking its reciprocal (1 / Tanθ), and vice versa. These relationships are fundamental in trigonometry and are widely used in solving various trigonometric problems and applications.

Cot-Tan Formula Solved Example

Example 1: Find the value for Cotθ if  Tanθ = 4/7.

Solution:

when Tanθ = 4/7, you can use the relationship:

Cotθ = 1 / Tanθ

Substitute the value of Tanθ:

Cotθ = 1 / (4/7)

Now, take the reciprocal:

Cotθ = 7/4

So, when Tanθ is 4/7, Cotθ is 7/4.

Also Check – Arithmetic Progressions Formula

Example 2: Find the values of Tanθ and Cotθ for a right triangle with an altitude of 9 units and a base of 13 units, you can use the following trigonometric ratios:

Tanθ = Opposite side / Adjacent side

Cotθ = Adjacent side / Opposite side

Solution:

In this case:

The opposite side is the altitude, which is 9 units.

The adjacent side is the base, which is 13 units.

Now, you can calculate the values:

Tanθ = Opposite side / Adjacent side = 9 / 13

Cotθ = Adjacent side / Opposite side = 13 / 9

So, for this right triangle, Tanθ is 9/13, and Cotθ is 13/9.

Also Check – Trigonometry Formula

Cot-Tan Formula Applications

The Cot-Tan Formula, which relates the cotangent (Cotθ) and tangent (Tanθ) trigonometric functions, has various applications in trigonometry and real-world problems, particularly those involving right triangles. Here are some common applications:

• Solving Right Triangle Problems: The  Cot-Tan Formula is used dealing with right triangles, the Cot-Tan Formula is often used to find missing sides or angles. Given one trigonometric ratio (Cotθ or Tanθ), you can easily calculate the other.
• Engineering and Construction: Engineers and architects frequently use trigonometry to design and construct structures. The Cot-Tan Formula is useful for determining angles and lengths in various building and construction projects.
• Navigation: Navigators, sailors, and pilots use trigonometric concepts to calculate distances and angles when navigating. The Cot-Tan Formula can help in solving navigation problems involving angles of elevation and depression.
• Surveying: Surveyors use trigonometry to measure distances and angles when mapping land, designing roads, or conducting boundary surveys. The Cot-Tan Formula aids in these calculations.
• Physics: In physics, especially when studying motion or forces at an inclined plane, the Cot-Tan Formula can be applied to analyze angles and accelerations.
• Astronomy: Astronomers use trigonometry to determine the positions of celestial objects. The Cot-Tan Formula can be applied to calculate angles in celestial observations.
• Computer Graphics: Computer graphics and video game designers use trigonometry extensively to create realistic animations and 3D models. The Cot-Tan Formula helps in determining angles of rotation and projection.
• Mechanical Engineering: Mechanical engineers use trigonometry to analyze and design mechanisms, linkages, and machines. The Cot-Tan Formula can be used to calculate angles and forces in mechanical systems.