
Trigonometry Formula: Trigonometry formulas encompass a collection of mathematical expressions involving trigonometric identities. They serve as essential tools for solving problems related to right-angled triangles, involving their sides and angles. In addition to their role in triangle-related problem-solving, these formulas also find extensive use in simplifying expressions, solving equations, and evaluating integrals.
These trigonometry formulas encompass a wide range of trigonometric functions such as sine, cosine, tangent, cosecant, secant, and cotangent for specified angles. To gain a comprehensive understanding, let's delve into these formulas, which encompass Pythagorean identities, product identities, co-function identities (angle transformations), sum and difference identities, double-angle identities, half-angle identities, and more. This comprehensive exploration will provide a deeper insight into their applications and utility.
Also Check - Rational Number FormulaWhat are Trigonometry Formulas?
Trigonometry formulas consist of mathematical relationships that connect the angles and sides within a right triangle. These formulas serve as crucial tools in trigonometry, enabling the solution of diverse problems involving angles, distances, and heights. Through the application of these formulas, it becomes possible to determine missing angles or sides within a right triangle.
Beyond the fundamental formulas, including the Pythagorean theorem, there exists a plethora of trigonometric identities and equations. These versatile mathematical tools play a pivotal role in simplifying expressions, solving equations, and evaluating integrals. As a result, these formulas hold immense significance for professionals such as engineers, mathematicians, and scientists across a wide range of disciplines.
Also Check - Linear Equation FormulaList of All Formulas of Trigonometry
Let's explore the following categories of trigonometry formulas:
- Fundamental Trig Ratio Formulas: These formulas pertain to the essential trigonometric ratios, such as sine, cosine, tangent, etc.
- Reciprocal Identities: These formulas describe the reciprocal relationships between trigonometric ratios.
- Trigonometric Ratio Table: This table provides the values of trigonometric functions for standard angles.
- Periodic Identities: These formulas facilitate the calculation of trigonometric values when angles shift by π/2, π, 2π, and so on.
- Co-function Identities: These formulas illustrate the connections between different trigonometric functions.
- Sum and Difference Identities: These formulas are utilized to determine the values of trigonometric functions for the sum or difference of angles.
- Half, Double, and Triple Identities: These formulas help find trigonometric function values for half, double, or triple angles.
- Sum to Product Identities : These formulas represent the product of trigonometric functions as their sum or vice versa.
- Inverse Trigonometry Formulas: These formulas are associated with inverse trigonometric functions like arcsine, arccosine, etc.
- Sine Law and Cosine Law: These laws are used to solve triangles and relate the sides and angles in non-right-angled triangles.
- Exploring these categories will provide a comprehensive understanding of trigonometry and its various applications.
Download PDF Trignometry Formula
Basic Trigonometry Formulas
Basic trigonometry formulas establish the relationships between trigonometric ratios and the corresponding sides of a right-angled triangle. In trigonometry, there are six fundamental trigonometric ratios, also known as trigonometric functions: sine (sin), cosine (cos), secant (sec), cosecant (csc), tangent (tan), and cotangent (cot). These ratios and their associated identities are derived using a right-angled triangle as a reference.
Using trigonometry formulas, we can determine the values of sine, cosine, tangent, secant, cosecant, and cotangent when provided with the dimensions of a right-angled triangle. These formulas allow us to calculate these trigonometric functions based on the triangle's angles and side lengths.
Also Check - Quadrilaterals FormulaReciprocal Identities
Cosecant, secant, and cotangent are the reciprocals of the fundamental trigonometric ratio’s sine, cosine, and tangent, respectively. These reciprocal identities are also established by referencing a right-angled triangle in trigonometry. These reciprocal trigonometric identities are derived from the original trigonometric functions, and they are valuable tools for simplifying trigonometric problems. The following trigonometry formulas for reciprocal identities are frequently employed to streamline such problems.
Also Check - Coordinate Geometry FormulaPythagorean Identities
The Pythagorean theorem asserts that in a right triangle, where 'c' represents the hypotenuse and 'a' and 'b' represent the two legs, the relationship is expressed as c² = a² + b². This fundamental theorem serves as the basis for deriving Pythagorean identities in trigonometry. These identities play a crucial role in converting one trigonometric ratio into another. The Pythagorean trigonometric identities are outlined below:
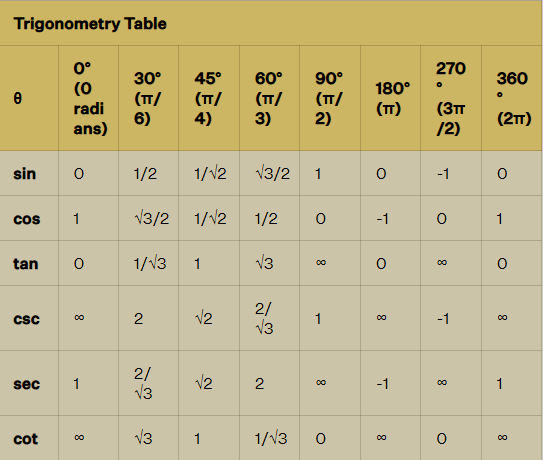
Trigonometric Ratio Table
Below is a table containing trigonometric formulas for commonly used angles in trigonometry problem-solving. This trigonometric ratios table aids in determining the values of trigonometric functions for standard angles, including 0°, 30°, 45°, 60°, and 90°.
Unit Circle Formulas
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. In trigonometry, it serves as a fundamental tool to establish the values of trigonometric functions for all angles, encompassing those beyond the standard range of 0 to 90 degrees.
Trigonometry Periodic Identities (in Radians)
Trigonometry formulas that encompass periodic identities enable the manipulation of angles by π/2, π, 2π, and so on. All trigonometric identities exhibit a cyclical nature, meaning they repeat their patterns after a certain interval. This period varies for different trigonometric formulas related to periodic identities. For instance, tan 30° is equivalent to tan 210°, but the same does not hold true for cos 30° and cos 210°. You can consult the provided trigonometry formulas to confirm the periodic behavior of sine and cosine functions in various quadrants.
First Quadrant:
- sin (π/2 – θ) = cos θ
- cos (π/2 – θ) = sin θ
- sin (2π + θ) = sin θ
- cos (2π + θ) = cos θ
Second Quadrant:
- sin (π/2 + θ) = cos θ
- cos (π/2 + θ) = – sin θ
- sin (π – θ) = sin θ
- cos (π – θ) = – cos θ
Third Quadrant:
- sin (π + θ) = – sin θ
- cos (π + θ) = – cos θ
- sin (3π/2 – θ) = – cos θ
- cos (3π/2 – θ) = – sin θ
Fourth Quadrant:
- sin (3π/2 + θ) = – cos θ
- cos (3π/2 + θ) = sin θ
- sin (2π – θ) = – sin θ
- cos (2π – θ) = cos θ
Co-function Identities (in Degrees)
The trigonometry formulas related to co-function identities establish connections between different trigonometric functions. These co-function trigonometry formulas are expressed in degrees as follows:
- sin(90° − x) = cos x
- cos(90° − x) = sin x
- tan(90° − x) = cot x
- cot(90° − x) = tan x
- sec(90° − x) = cosec x
- cosec(90° − x) = sec x
To express these co-function identities in radians, you can substitute 90° with π/2 in the above formulas.
Sum and Difference Identities
The sum and difference identities encompass a set of trigonometry formulas involving expressions like sin(x + y), cos(x - y), cot(x + y), and others. These identities are expressed as follows:
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x + y) = cos(x)cos(y) - sin(x)sin(y)
- tan(x + y) = (tan x + tan y)/(1 - tan x • tan y)
- sin(x – y) = sin(x)cos(y) - cos(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- tan(x − y) = (tan x - tan y)/(1 + tan x • tan y)
These trigonometric identities are valuable tools for simplifying expressions involving the sum or difference of angles in trigonometry.
Multiple and Sub-Multiple Angles
Trigonometry formulas for multiple and sub-multiple angles are employed to determine the values of trigonometric functions for various angle multiples, such as half angle, double angle, triple angle, and so forth.
Half-Angle Identities
The half angle trigonometric formulas involve x/2 and are as follows.
- sin (x/2) = ±√[(1 - cos x)/2]
- cos (x/2) = ± √[(1 + cos x)/2]
- tan (x/2) = ±√[(1 - cos x)/(1 + cos x)] (or) tan (x/2) = (1 - cos x)/sin x
Double Angle Identities
- sin (2x) = 2sin(x) • cos(x) = [2tan x/(1 + tan 2 x)]
- cos (2x) = cos 2 (x) - sin 2 (x) = [(1 - tan 2 x)/(1 + tan 2 x)] = 2cos 2 (x) - 1 = 1 - 2sin 2 (x)
- tan (2x) = [2tan(x)]/ [1 - tan 2 (x)]
- sec (2x) = sec 2 x/(2 - sec 2 x)
- cosec (2x) = (sec x • cosec x)/2
Triple Angle Identities
- sin 3x = 3sin x - 4sin 3 x
- cos 3x = 4cos 3 x - 3cos x
- tan 3x = [3tanx - tan 3 x]/[1 - 3tan 2 x]
Sum and Product Identities
Trigonometric formulas for sum or product identities are utilized to express the sum of two trigonometric functions as their product or to represent their product as a sum, offering versatile ways to manipulate trigonometric expressions.
Product to Sum Formulas
- sinx ⋅ cosy = [sin(x + y) + sin(x − y)]/2
- cosx ⋅ cosy = [cos(x + y) + cos(x − y)]/2
- sinx ⋅ siny = [cos(x − y) − cos(x + y)]/2
Sum to Product Formulas
The combination of two acute angles A and B can be presented through the trigonometric ratios, in the below trigonometry formulas.
- sinx + siny = 2[sin((x + y)/2)cos((x − y)/2)]
- sinx − siny = 2[cos((x + y)/2)sin((x − y)/2)]
- cosx + cosy = 2[cos((x + y)/2)cos((x − y)/2)]
- cosx − cosy = −2[sin((x + y)/2)sin((x − y)/2)]
Inverse Trigonometry Formulas
By employing inverse trigonometry formulas, trigonometric ratios are reversed to define inverse trigonometric functions. For instance, if we have sin θ = x, we can find θ by using the inverse sine function: θ = sin ⁻ ¹(x). It's important to note that x in this context can take on various values, including whole numbers, decimals, fractions, and exponents, allowing for a wide range of possible inputs and solutions.
- sin -1 (-x) = -sin -1 x
- cos -1 (-x) = π - cos -1 x
- tan -1 (-x) = -tan -1 x
- cosec -1 (-x) = -cosec -1 x
- sec -1 (-x) = π - sec -1 x
- cot -1 (-x) = π - cot -1 x
Sine and Cosine Laws
Sine Law: The sine law and the cosine law establish relationships between the sides and angles of a triangle. The sine law provides a ratio between a side and the angle opposite that side. For instance, it calculates the ratio for side 'a' and its corresponding angle 'A':
(sin A)/a = (sin B)/b = (sin C)/c
Cosine Law: The cosine law assists in determining the length of one side when the lengths of the other two sides and the included angle are known. For instance, it allows us to find the length 'a' using the lengths 'b' and 'c' and the included angle 'A':
a 2 = b 2 + c 2 - 2bc cosA
b 2 = a 2 + c 2 - 2ac cosB
c 2 = a 2 + b 2 - 2ab cosC
Here, 'a,' 'b,' and 'c' represent the lengths of the triangle's sides, while 'A,' 'B,' and 'C' represent the angles of the triangle.
Examples Using Trigonometry Formulas
Example 1: Given the trigonometric ratio tan θ = 5/12, determine the trigonometric ratio cosec θ.
Solution:
Given: tan θ = 5/12
This implies:
Perpendicular/ Base = 5/12
Perpendicular = 5 and Base = 12
Using the Pythagorean theorem:
Hypotenuse 2 = Perpendicular 2 + Base 2
Hypotenuse 2 = 5 2 + 12 2
Hypotenuse 2 = 25 + 144
Hypotenuse = √169
Hypotenuse = 13
Now, employing trigonometric formulas:
cosec θ = Hypotenuse/Perpendicular = 13/5
Answer: cosec θ = 13/5
Example 2: Determine the value of sin 15º.
Hint: Use sum and difference trigonometric formulas.
Solution:
sin 15º
= sin (45º - 30º)
= sin 45ºcos 30º - cos 45ºsin 30º
= [(1/√2) × (√3/2)] - [(1/√2) × (1/2)] = (√3 - 1)/(2√2)
Answer: sin 15° = (√3 - 1)/(2√2)
Example 3: If sin θ cos θ = 5, determine the value of (sin θ + cos θ)^2 using trigonometry formulas.
Solution:
(sin θ + cos θ)^2
= sin^2θ + cos^2θ + 2sinθcosθ
= 1 + 2(5) = 1 + 10 = 11
Answer: (sin θ + cos θ)^2 = 11
Trigonometry Formula FAQs
What does Trigonometry mean?
Explain the term Basic Trigonometry Formula.
Define the Trigonometry Ratio Formula.
Explain the Addition Trigonometry Formula.










