
EMF of a Cell: The electromotive force of a cell is known as EMF of a Cell( EMF). It refers to the utmost potential difference between the two electrodes within the cell. Another way to express it is as the overall voltage generated by the oxidation and reduction of half-reactions. The primary application of the EMF of a Cell is to determine the galvanic or non-galvanic nature of an electrochemical cell.
What Is an Electrochemical Cell?
An electrochemical cell is a device designed to produce electricity through a chemical reaction. In essence, it can be described as a mechanism that transforms chemical energy into electrical energy. The operation of an electrochemical cell necessitates a chemical process that involves the exchange of electrons, commonly known as a redox reaction.
Each cell is characterized by its voltage, and a specific type of cell generates a consistent voltage regardless of its physical size. The only factor influencing the cell's voltage is its chemical composition, assuming the cell operates under ideal conditions.
In practice, the cell's voltage may deviate from this ideal value due to various factors such as temperature variations and changes in concentration. To determine the electromotive force (EMF of a Cell) of a given cell, one can employ the Nernst equation, developed by Walther Nernst, provided the standard cell potential is known.
Types of Electrochemical Cell
Galvanic Cell: The Galvanic Cell, named after the Italian scientist Luigi Galvani, is a fundamental electrochemical cell that serves as the basis for many other electrochemical cells, such as the Daniell cell. It comprises two dissimilar metallic conductors, referred to as electrodes, each immersed in its own ionic solution. These individual setups are termed half-cells. A single half-cell cannot produce a potential difference on its own, but when combined, they generate a potential difference. To chemically connect two cells, a salt bridge is employed. It facilitates the transfer of the necessary electrons from the electron-deficient half-cell to the electron-rich half-cell.
For further insight, let's explore the theory of the Daniell cell and derive the Nernst equation for it.
Daniell Cell: The Daniell cell is a modification of the galvanic cell and consists of zinc and copper electrodes submerged in zinc sulfate and copper sulfate solutions, respectively. A salt bridge connects the two half-cells, with the zinc electrode serving as the anode and the copper electrode as the cathode.
Zinc, having a higher oxidation potential than copper, undergoes oxidation, resulting in the generation of two electrons and a zinc ion. This causes the zinc electrode to acquire a negative potential due to the release of electrons, making it the anode.
On the other hand, copper experiences reduction due to its higher reduction potential. In the copper half-cell, the copper ions in the solution accept two electrons from the electrode, leading to the deposition of copper metal on the electrode. Since this electrode consumes electrons, it is considered the positive electrode, and it is referred to as the cathode.
The anode reaction is represented as follows:
Zn(s) → Zn 2+ (aq) + 2e –
The cathode reaction is represented as follows:
Cu 2+ (aq) +2e – → Cu(s)
The combined cell reaction or overall cell reaction is as follows:
Zn(s) + Cu 2+( aq) → Zn 2+ (aq) + Cu(s)
Electrode Potential
When a metal electrode is submerged in a solution containing its own ions, it results in the establishment of a potential difference at the interface, known as the electrode potential.
Let's take the example of a zinc electrode immersed in a zinc sulfate solution. Here, the zinc metal undergoes oxidation, releasing two electrons into the solution. The presence of electrons within the electrode and ions within the solution creates a potential difference. Conversely, copper develops a positive potential in a similar manner. The combined effect of these two half-cells contributes to the cell potential.
In practice, determining the potential of a single half-cell alone is not feasible. To ascertain the potential of a single half-cell, a standard half-cell with a predefined potential value is always necessary. The standard hydrogen electrode (SHE) serves as an illustrative example of such a standard half-cell, with its potential value inherently set at zero volts. This standard hydrogen electrode is connected to the unknown half-cell, and the resulting potential difference is measured. Since the SHE possesses zero volts, the measured value corresponds to the potential difference of the unknown half-cell.
The diagram below outlines the procedure for determining the standard electrode potential of zinc.
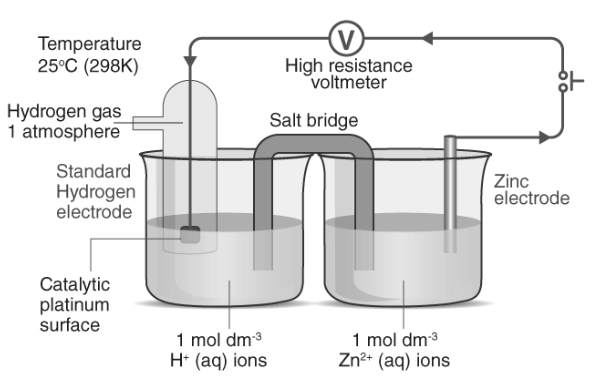
Electrochemical Series
EMF of a Cell. Furthermore, the electrochemical series is created by calculating and arranging the standard potential values of different metals in ascending order of their potential.
The electrochemical series plays a crucial role in determining cell potential and aids in the selection of electrode materials when building a cell.
The electrochemical series table displays the positioning of various elements based on their reduction potential in increasing order. Typically, lithium has the lowest reduction potential, while fluorine possesses the highest. Hydrogen serves as the reference point with a zero reduction potential, as all other elements are compared against hydrogen to determine their standard electrode potential.
Representation of an Electrochemical Cell
An electrochemical cell can be symbolized using special notations, which prove helpful in comprehending its composition and the quantities involved.
For instance, the Daniell cell mentioned above can be represented as follows:
Anode: Zn | Zn 2+ (1M)
Cathode: Cu 2+ (1M) | Cu
Breaking it down:
The left side of the notation signifies the anode, where Zn undergoes conversion by releasing two electrons per zinc atom. The 1M concentration of the solution is also included in the representation.
On the right side, the cathode is depicted. Here, the electrolyte accepts a pair of electrons from the electrode and transforms into Cu metal. Similarly, the 1M copper sulfate solution is specified.
To connect these two half-cells chemically, vertical bars are used, representing the salt bridge:
Zn | Zn 2+ (1M) || Cu 2+ (1M) | Cu
Determining the Cell Potential of an Electrochemical Cell
The cell potential, often referred to as EMF of a Cell in an electrochemical cell can be computed by using the electrode potentials of its two half-cells. Typically, three methods are employed for this calculation:
By accounting for the oxidation potential of the anode and the reduction potential of the cathode.
By considering the reduction potentials of both electrodes.
By taking into account the oxidation potentials of both electrodes.
The standard cell potential (ΔE o ) of a galvanic cell can be calculated by evaluating the standard reduction potentials (E o ) of the two respective half-cells.
E o cell = E o red + E o ox
Alternatively,
E o cell = E o Cathode + E o Anode
The cell potential of a galvanic cell can be defined as the potential of the half-cell on the right side (cathode) minus the potential of the half-cell on the left side (anode).
In the case of the Daniell cell,
The cell potential of the Daniell cell, denoted as Ecell, can be calculated as follows:
Ecell = Ecu2+ | Cu - Ezn | Zn2+
The Nernst equation establishes a connection between the equilibrium state potential of a half-cell and various factors, including the standard electrode potential of the half-cell, temperature, reaction coefficients, and the activity of the reacting species.
For an electrode reaction represented as Mn+ + n e– → M(s), the equilibrium state EMF of a Cell (EMF) is expressed as:
In this context, where EMn+| M represents the half-cell potential, EOMn+| M is the standard electrode potential of the half-cell, [ M ] signifies the molar concentration of the metal, [ Mn+ ] denotes the molar concentration of the metal ion, R stands for the universal gas constant (8.314 J/K/mole), T represents the temperature in Kelvin, n signifies the number of electrons involved in the reaction, and F represents Faraday's constant (96500 C/mole).
Additionally, considering that the molar concentration of a metallic solid is conventionally set to one:
[ M ] = 1
Substituting the values of R, F, and T = 298K (room temperature) into the equation leads to a refined expression:
EMn+| M = EOMn+| M – 0.059 / n × log(1 / [ Mn+ ])
Now, let's consider an arbitrary cell comprising two metals, M and N, with M having a greater reduction potential than N. Consequently, M serves as the cathode, while N functions as the anode.
For the anode reaction:
N → N n+ + ne –
And for the cathode reaction:
M n+ + ne – → M
As previously established,
The cell potential of a galvanic cell can be determined as the potential of the half-cell on the right side (cathode) minus the potential of the half-cell on the left side (anode).
Hence, the EMF of a Cell( EMF) of the cathode half-cell is calculated as:
E M n+ | M = E O M n+ | M – 0.059 / n × log(1 / [ M n+ ])
The EMF of a Cell (EMF) of the anode half-cell is determined as:
E N n+ | N = E O N n+ | N – 0.059 / n × log(1 / [ N n+ ])
C onsequently, the cell potential of the Galvanic cell can be expressed as:
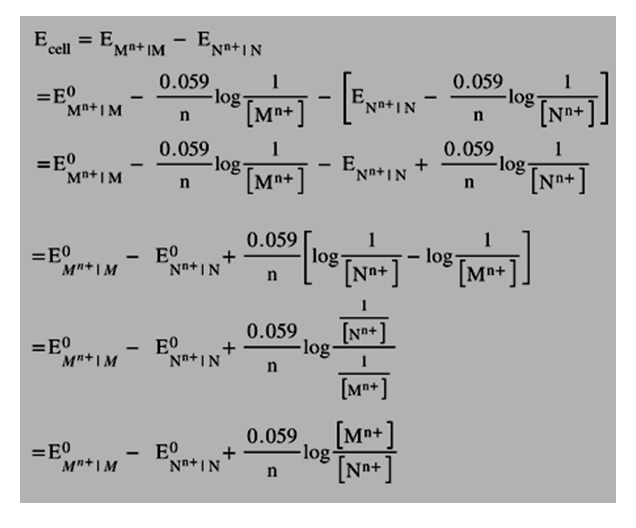
We have the following equation:
E O M n+ | M – E O N n+ | N = E O cell
This represents the standard cell potential of a galvanic cell under standard conditions (STP).
Therefore, we can express EMF of a Cell as:
E cell = E O cell + 0.059 / n × log [ M n+ ] / [ N n+ ]
For the Daniell cell:
Since the process involves 2 electrons, n = 2.
E cell = E O cell + 0.059 / 2 × log [ Cu 2+ ] / [ Zn 2+ ]
Referring to the electrochemical series:
E O cell = E O cathode – E O anode = E Cu 2+ | Cu - E O Zn 2+ | Zn = 0.34 – (-0.76) = 1.1 V
Substituting this value, we get:
E cell = 1.1 + 0.059 / 2 × log [ Cu 2+ ] / [ Zn 2+ ]
| Related Links | |
| Ammonium Phosphate Formula | Arsenic Acid Formula |
| Strontium Sulfate Formula | Strontium Chloride Formula |
EMF of a Cell FAQs
What is EMF in the context of a cell?
Why is EMF important in electrochemistry?
What are the units of EMF?
How is the EMF of a cell related to its half-cell potentials?










