NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4 (Limits and Derivatives)
Krati Saraswat20 Feb, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4 (Limits and Derivatives)
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4 Limits and Derivatives is prepared by the academic team of PW. We have prepared NCERT Solutions for all exercise of chapter 13. Below are step-by-step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4 of Limits and Derivatives.NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4 Overview
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4 cover several important topics. It is highly recommended for students to review each topic thoroughly in order to gain a comprehensive understanding of the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the result of dedicated efforts by the Physics Wallah teachers aimed at assisting students in grasping the concepts covered in this chapter. By going through and practicing these solutions, the objective is for students to achieve excellent results in their exams effortlessly.NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4:
Question 1. State which of the following are not the probability distributions of a random variable. Give reasons for your answer. (i)| X | 0 | 1 | 2 |
| P (X) | 0.4 | 0.4 | 0.2 |
| X | 0 | 1 | 2 | 3 | 4 |
| P (X) | 0.1 | 0.5 | 0.2 | – 0.1 | 0.3 |
| Y | – 1 | 0 | 1 |
| P (Y) | 0.6 | 0.1 | 0.2 |
| Z | 3 | 2 | 1 | 0 | – 1 |
| P (Z) | 0.3 | 0.2 | 0.4 | 0.1 | 0.05 |
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3
Question 2. An urn contains 5 red and 2 black balls. Two balls are randomly selected. Let X represents the number of black balls. What are the possible values of X? Is X a random variable? Solution : There two balls may be selected as BR, RB, BR, BB, where R represents red ball and B represents black ball. Variable X has the value 0, 1, 2, i.e., there may be no black ball, may be one black ball or both the balls are black. Question 3. Let X represents the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are possible values of X? Solution : A coin is tossed six times and X represents the difference between the number of heads and the number of tails. ∴ X (6 H, 0T) = |6 - 0| = 6 X (5 H, 1 T) = |5 - 1| = 4 X (4 H, 2 T) = |4 - 2| = 2 X (3 H, 3 T) = 3 - 3| = 0 X (2 H, 4 T) = |2 - 4| = 2 X (1 H, 5 T) = |1 - 5| = 4 X (0H, 6 T) = | 0 - 6| = 6 Thus, the possible values of X are 6, 4, 2, and 0. Question 4. Find the probability distribution of: (i) Number of heads in two tosses of a coin. (ii) Number of tails in the simultaneous tosses of three coins. (iii) Number of heads in four tosses of a coin. Solution : (i) When one coin is tossed twice, the sample space is {HH, HT, TH, TT} Let X represent the number of heads. ∴ X (HH) = 2, X (HT) = 1, X (TH) = 1, X (TT) = 0 Therefore, X can take the value of 0, 1, or 2. It is known that, P(HH) = P(HT) = P(TH) = P(TT) = 1/4 P (X = 0) = P (TT) = 1/4 P (X = 1) = P (HT) + P (TH) = 14 + 1/4 = 1/2 P (X = 2) = P (HH) = 1/4 Thus, the required probability distribution is as follows.-
X
0
1
2
P (X)
1/4
1/2
1/4
-
X
0
1
2
3
P (X)
1/8
3/8
3/8
1/8
-
X
0
1
2
3
4
P (X)
1/16
1/4
3/8
1/4
1/16
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2
Question 5. Find the probability distribution of the number of success in two tosses of a die where a success is defined as: (i) number greater than 4. (ii) six appears on at least one die. Solution : When a die is tossed two times, we obtain (6 × 6) = 36 number of observations. Let X be the random variable, which represents the number of successes. (i) Here, success refers to the number greater than 4. P (X = 0) = P (number less than or equal to 4 on both the tosses) = 4/6 X 4/6 = 4/9 P (X = 1) = P (number less than or equal to 4 on first toss and greater than 4 on second toss) + P (number greater than 4 on first toss and less than or equal to 4 on second toss) = 4/6 X 2/6 + 4/6 X 2/6 = 4/9 P (X = 2) = P (number greater than 4 on both the tosses) = 2/6 X 2/6 = 1/9 Thus, the probability distribution is as follows.-
X
0
1
2
P (X)
4/9
4/9
1/9
(ii) Here, success means six appears on at least one die.
P (Y = 0 ) = P (six appears on none of the dice) = 5/6 x 5/6 = 25/36 P (Y = 1) = P (six appears on at least one of the dice) = 1/6 x 5/6 + 5/6 x 1/6 + 1/6 x 1/6 = 11/36 Thus, the required probability distribution is as follows.|
Y |
0 |
1 |
|
P (Y) |
25/36 |
11/26 |
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.1
Question 6. From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs. Solution : It is given that out of 30 bulbs, 6 are defective. ⇒ Number of non-defective bulbs = 30 − 6 = 24 4 bulbs are drawn from the lot with replacement. Let X be the random variable that denotes the number of defective bulbs in the selected bulbs.
Therefore, the required probability distribution is as follows.
|
X |
0 |
1 |
2 |
3 |
4 |
|
P (X) |
256/625 |
256/625 |
96/625 |
16/625 |
1/625 |
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.5
Question 7. A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails. Solution : Let the probability of getting a tail in the biased coin be x . ∴ P (T) = x ⇒ P (H) = 3 x For a biased coin, P (T) + P (H) = 1
When the coin is tossed twice, the sample space is {HH, TT, HT, TH}.
Let X be the random variable representing the number of tails.
∴ P (X = 0) = P (no tail) = P (H) × P (H) = 3/4 x 3/4 = 9/16
P (X = 1) = P (one tail) = P (HT) + P (TH)
= 3/4 . 1/4 + 1/4 . 3/4
= 3/16 + 3/16= 3/8
P (X = 2) = P (two tails) = P (TT) = 1/4 x 1/4 = 1/16
Therefore, the required probability distribution is as follows.
|
X |
0 |
1 |
2 |
|
P (X) |
9/16 |
3/8 |
1/16 |
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P (X) | 0 | k | 2k | 2k | 3k | k 2 | 2 k 2 | 7k 2 + k |
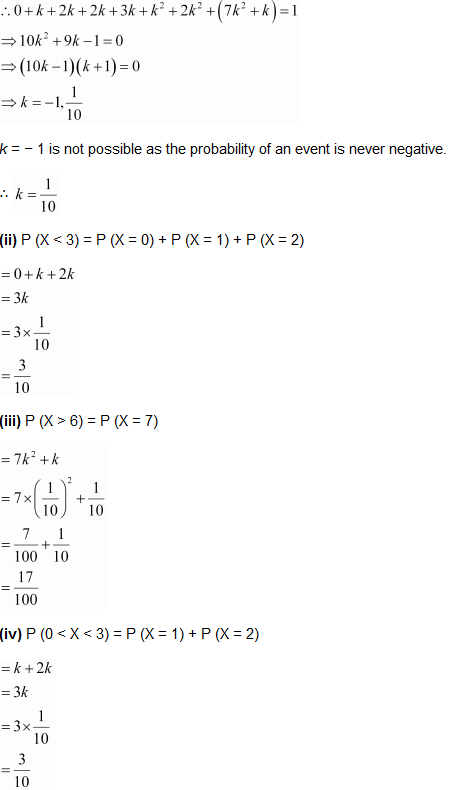Question
9. The random variable X has a probability distribution P(X) of the following form, where k is some number:
(a) Determine the value of k .
(b) Find P(X < 2), P(X ≥ 2), P(X ≥ 2).
Solution : (a) It is known that the sum of probabilities of a probability distribution of random variables is one. ∴ k + 2 k + 3 k + 0 = 1 ⇒ 6 k = 1 ⇒ k =1/6 (b) P(X < 2) = P(X = 0) + P(X = 1) = k + 2k = 3k =3/6 = 1/2
10. Find the mean number of heads in three tosses of fair coin.
Solution :
Let X denote the success of getting heads.
Therefore, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
It can be seen that X can take the value of 0, 1, 2, or 3
Therefore, the required probability distribution is as follows.
| X |
0 |
1 |
2 |
3 |
|
P(X) |
1/8 |
3/8 |
3/8 |
1/8 |
Question
11. Two dice are thrown simultaneously. If X denotes the number of sixes, find expectation of X.
Solution :
Two dice thrown simultaneously is the same the die thrown 2 times.
Here, X represents the number of sixes obtained when two dice are thrown simultaneously. Therefore, X can take the value of 0, 1, or 2.
∴ P (X = 0) = P (not getting six on any of the dice) = 25/36
P (X = 1) = P (six on first die and no six on second die) + P (no six on first die and six on second die)
=2(1/6 x 5/6) = 10/36
P (X = 2) = P (six on both the dice) =1/36
Therefore, the required probability distribution is as follows.
|
X |
0 |
1 |
2 |
|
P(X) |
25/36 |
10/36 |
1/36 |
|
X |
2 |
3 |
4 |
5 |
6 |
|
P(X) |
1/15 |
2/15 |
1/5 |
4/15 |
1/3 |
Question
13. Let X denotes the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.
Solution :
When two fair dice are rolled, 6 × 6 = 36 observations are obtained.
P(X = 2) = P(1, 1) = 1/36
P(X = 3) = P (1, 2) + P(2, 1) = 2/36 = 1/18
P(X = 4) = P(1, 3) + P(2, 2) + P(3, 1) = 3/36 = 1/12
P(X = 5) = P(1, 4) + P(2, 3) + P(3, 2) + P(4, 1) = 4/36 = 1/9
P(X = 6) = P(1, 5) + P (2, 4) + P(3, 3) + P(4, 2) + P(5, 1) = 5/36
P(X = 7) = P(1, 6) + P(2, 5) + P(3, 4) + P(4, 3) + P(5, 2) + P(6, 1) = 6/36 = 1/6
P(X = 8) = P(2, 6) + P(3, 5) + P(4, 4) + P(5, 3) + P(6, 2) = 5/36
P(X = 9) = P(3, 6) + P(4, 5) + P(5, 4) + P(6, 3) = 4/36 = 1/9
P(X = 10) = P(4, 6) + P(5, 5) + P(6, 4) = 3/36 = 1/12
P(X = 11) = P(5, 6) + P(6, 5) = 2/36 = 1/18
P(X = 12) = P(6, 6) = 1 x 36
Therefore, the required probability distribution is as follows.
|
X |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
P(X) |
1/36 |
1/18 |
1/12 |
1/9 |
5/36 |
1/6 |
5/36 |
1/9 |
1/12 |
1/18 |
1/36 |
Question
14. A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. One student is selected in such a manner that each has the same chance of being chosen and the age X of the selected student is recorded. What is the probability distribution of the random variable X? Find mean, variance and standard deviation of X.
Solution :
There are 15 students in the class. Each student has the same chance to be chosen. Therefore, the probability of each student to be selected is 1/15.
The given information can be compiled in the frequency table as follows.
|
X |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
f |
2 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
|
X |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
f |
2/15 |
1/15 |
2/15 |
3/15 |
1/15 |
2/15 |
3/15 |
1/15 |
Question
15. In a meeting 70% of the members favour a certain proposal, 30% being opposed. A member is selected at random and we let X = 0 if the opposed and X = 1 if he is in favour. Find E (X) and Var (X).
Solution :
It is given that P(X = 0) = 30% = 30/100 = 0.3
P(X = 1) = 70% = 70/100 = 0.7
Therefore, the probability distribution is as follows.
|
X |
0 |
1 |
|
P(X) |
0.3 |
0.7 |
= 0.7 − (0.7)
2
= 0.7 − 0.49
= 0.21
Choose the correct answer in each of the following:
Question
16. The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is:
(A) 1
(B) 2
(C) 5
(D) 8/3
Solution :
Let X be the random variable representing a number on the die.
The total number of observations is six.
Therefore, the probability distribution is as follows.
|
X |
1 |
2 |
5 |
|
P(X) |
1/2 |
1/3 |
1/6 |
Therefore, option (B) is correct.
Question
17. Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. What is the value of E(X)?
(A) 37/221
(B) 5/13
(C) 1/13
(D) 2/13
Solution :
Let X denote the number of aces obtained. Therefore, X can take any of the values of 0, 1, or 2.
In a deck of 52 cards, 4 cards are aces. Therefore, there are 48 non-ace cards.
Therefore, option (D) is correct.
NCERT Solutions For Class 12 Maths Chapter 13 Exercise 13.4 FAQs
What is the purpose of limits and derivatives?
What is the principle of derivatives limits?
Is limits and derivatives important for class 12?
Why do we use limit?
Why limits are used in integration?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
