NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in chapter 13.
Krati Saraswat19 Feb, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise Limits and Derivatives is prepared by the academic team of pw. We have prepared NCERT Solutions for all exercise of chapter 13. Given below is step by step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise of Limits and Derivatives.NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.4
NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise Overview
NCERT Solutions for Class 12 Maths Chapter 12 Miscellaneous Excercise addresses these significant subjects. In order to fully comprehend the concepts presented in the chapter and make effective use of the provided solutions, it is recommended that students go over each topic in great detail. The intention is for students to effortlessly achieve excellent exam scores after reviewing and practicing these responses.NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise:
Question 1. A and B are two events such that P (A) ≠ 0. Find P (B/A) if: (i)A is a subset of B (ii) A ∩ B = Φ Solution : A and B are two events such that P (A) ≠ 0 To find: P(A) (i) A is a subset of B
(ii)
A ∩ B = Φ
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3
Question 2. A couple has two children. (i)Find the probability that both children are males I it is known that at least one of the children is male. (ii)Find the probability that both children are females if it is known that the elder child is a female. Solution : If a couple has two children, then the sample space is S = {( b , b ), ( b , g ), ( g , b ), ( g , g )} (i) Let E and F respectively denote the events that both children are males and at least one of the children is a male.
(ii) Let A and B respectively denote the events that both children are females and the elder child is a female.
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.2
Question 3. Suppose that 5% of men and 0.25% of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females. Solution : It is given that 5% of men and 0.25% of women have grey hair. Therefore, percentage of people with grey hair = (5 + 0.25) % = 5.25% ∴ Probability that the selected haired person is a male = 5/5.25 = 20/21NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.1
Question 4. Suppose that 90% of people are right-handed. What is the probability that at most of 6 of a random sample of 10 people are right-handed? Solution : A person can be either right-handed or left-handed. It is given that 90% of the people are right-handed.
Using binomial distribution, the probability that more than 6 people are right-handed is given by,
Therefore, the probability that at most 6 people are right-handed
= 1 − P (more than 6 are right-handed)
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.5
Question 5 . An urn contains 25 balls of which 10 balls bear a mark ‘X’ and the remaining 15 bear a mark ‘Y’. A ball is drawn at random from the urn, its mark noted down and it is replaced. If 6 balls are drawn in this way, find the probability that: (i)all will bear ‘X’ mark. (ii)not more than 2 will bear ‘Y’ mark. (iii)at least one ball will bear ‘Y’ mark. (iv)the number of balls with ‘X’ mark and ‘Y’ mark will be equal. Solution : Total number of balls in the urn = 25 Balls bearing mark ‘X’ = 10 Balls bearing mark ‘Y’ = 15 p = P (ball bearing mark ‘X’) =10/25 = 2/5 q = P (ball bearing mark ‘Y’) =15/25 = 3/5 Six balls are drawn with replacement. Therefore, the number of trials are Bernoulli trials. Let Z be the random variable that represents the number of balls with ‘Y’ mark on them in the trials. Clearly, Z has a binomial distribution with n = 6 and p =2/5.
Question
6. In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5/6 What is the probability that he will knock down fewer than 2 hurdles?
Solution :
Let
p
and
q
respectively be the probabilities that the player will clear and knock down the hurdle.
Let X be the random variable that represents the number of times the player will knock down the hurdle.
Therefore, by binomial distribution, we obtain
Question
7. A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.
Solution :
The probability of getting a six in a throw of die is 1/6 and not getting a six is 5/6.
Let p = 1/6 and q = 5/6
The probability that the 2 sixes come in the first five throws of the die is
∴ Probability that third six comes in the sixth throw =
Question
8. If a leap year is selected at random, what is the change that it will contain 52 Tuesday?
Solution :
A leap year has 366 days which means 52 complete weeks and 2 days. If any one of these two days in a Tuesday then the year will have 53 Tuesdays.
Number of total days in a week = 7
Number of favourable days = 2
Therefore, P (the year will have 53 Tuesday) = 2/7
Question
9. An experiment succeeds twice as often as it fails. Find the probability that in the next six trails, there will be at least 4 successes.
Solution :
The probability of success is twice the probability of failure.
Let the probability of failure be
x
.
∴ Probability of success = 2
x
Let X be the random variable that represents the number of successes in six trials.
By binomial distribution, we obtain
Question
10. How many times must a man toss a fair coin so that the probability of having at least one head is more than 90%?
Solution :
Let the man toss the coin
n
times. The
n
tosses are
n
Bernoulli trials.
Probability (
p
) of getting a head at the toss of a coin is 1/2.
∴
p
= 1/2 ⇒
q
= 1/2
It is given that,
P (getting at least one head) > 90/100
P (
x
≥ 1) > 0.9
⇒ 1 − P (
x
= 0) > 0.9
The minimum value of
n
that satisfies the given inequality is 4.
Thus, the man should toss the coin 4 or more than 4 times.
Question
11. In a game a man wins a rupee for a six and looses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amounts he wins/looses.
Solution :
When a die is thrown, then probability of getting a six = 16
then, probability of not getting a six = 1 - 16 = 56
If the man gets a six in the first throw, then
probability of getting a six = 16
If he does not get a six in first throw, but gets a six in second throw, then
probability of getting a six in the second throw = 56×16 = 536
If he does not get a six in the first two throws, but gets in the third throw, then
probability of getting a six in the third throw = 56×56×16 = 25216
probability that he does not get a six in any of the three throws = 56×56×56 = 125216
In the first throw he gets a six, then he will receive Re 1.
If he gets a six in the second throw, then he will receive Re (1 - 1) = 0
If he gets a six in the third throw, then he will receive Rs(-1 - 1 + 1) = Rs (-1),
that means he will lose Re 1 in this case.
Expected value = 16×1 + 56×16 × 0 + 56×56×16×-1 = 11216
So, he will loose Rs 11216.
Question
12. Suppose we have four boxes A, B, C and D containing coloured marbles as given below:
| Box | Marble colour | ||
| Red | White | Black | |
| A B C D | 1 6 8 0 | 6 2 1 6 | 3 2 1 4 |
Probability that the red marble is from box B is P (E
B
|R).
Probability that the red marble is from box C is P (E
C
|R).
Question
13. Assume that the chances of a patient having a heart attack is 40%. It is also assumed that a meditation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chances by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga.
Solution :
A patient has options to have the treatment of yoga and meditation and that of prescription of drugs.
Let these events be denoted by E
1
and E
2
i.e.,
E
1
= Treatment of yoga and meditation
E
2
= Treatment of prescription of certain drugs
P (E
1
) = P (E
2
) = 1/2
Let A denotes that a person has heart attack, then P (A) = 40% = 0.40
Yoga and meditation reduces heart attack by 30.
Inspite of getting yoga and meditation treatment heart risk is 70% of 0.40
P (A|E
1
) = 0.40 x 0.70 = 0.28
Also, Drug prescription reduces the heart attack rick by 25%
Even after adopting the drug prescription hear rick is 75% of 0.40
P (A|E
2
) = 0.40 x 0.75 = 0.30
Question
14. If each element of a second order determinant is either zero or one, what is the probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability 1/2).
Solution :
There are four entries in a determinant of 2 x 2 order. Each entry may be filled up in two ways with 0 or 1.
Number of determinants that can be formed = (2)
4
= 16
The value of determinants is positive in the following cases:
Therefore, the probability that the determinant is positive = 3/16
Question
15.
An electronic assembly consists of two sub-systems say A and B. From previous testing procedures, the following probabilities are assumed to be known:
P (A fails) = 0.2
P (B fails alone) = 0.15
P (A and B fail) = 0.15
Evaluate the following probabilities.
Solution :
Let the event in which A fails and B fails be denoted by E
A
and E
B
.
P (E
A
) = 0.2
P (E
A
∩ E
B
) = 0.15
P (B fails alone) = P (E
B
) − P (E
A
∩ E
B
)
⇒ 0.15 = P (E
B
) − 0.15
⇒ P (E
B
) = 0.3
(ii) P (A fails alone) = P (E
A
) − P (E
A
∩ E
B
)
= 0.2 − 0.15
= 0.05
Question
16. Bag I contains 3 Red and 4 Black balls and B II contains 4 Red and % Black balls. One ball is transferred from Bag I to bag II and then a ball is drawn from bag II. The ball so drawn is found to be Red in colour. Find the probability that the transferred ball is Black.
Solution :
Let E
1
= Ball transferred from Bag I to Bag II is red
E
2
= Ball transferred from Bag I to Bag Ii is black
A = Ball drawn from Bag II is red in colour
P (E
1
) =3/7 and P (E
2
) = 4/7
Let A be the event that the ball drawn is red.
When a red ball is transferred from bag I to II,
P (A | E
1
) = 5/10 = 1/2
When a black ball is transferred from bag I to II,
P (A | E
2
) = 4/10 = 2/5
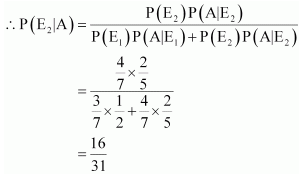
Choose the correct answer in each of the following:
Question 17. If A and B are two events such that P (A) ≠ 0 and P(B|A) = 1, then: (A) A ⊂ B (B) B ⊂ A(C) B = Φ
(D) A = Φ
Solution :
Therefore, option (A) is correct.
Question
18.
If P (A|B) > P (A), then which of the following is correct:
(A) P (B|A) < P (B)
(B) P (A ∩ B) < P (A).P (B)
(C) P (B|A) > P (B)
(D) P (B|A) = P (B)
Solution :
Therefore, option (C) is correct.
Question
19. If A and B are any two events such that P (A) + P (B) – P (A and B) = P (A), then
(A) P (B|A) = 1
(B) P (A|B) = 1
(C) P (B|A) = 0
(D)P (A|B) = 0
Solution :
Therefore, option (B) is correct.
NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise FAQs
Is probability class 12 difficult?
The difficulty level of Probability in Class 12 Mathematics can vary depending on individual students' understanding of the concepts, their aptitude for mathematical reasoning, and the teaching methods employed by their instructors. Some students may find Probability challenging due to its abstract nature and the need for a solid grasp of mathematical concepts such as permutations, combinations, and probability distributions.
How can students use NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise effectively?
Students can use the solutions to verify their answers, understand the correct approach to solving problems, and learn from any mistakes they may have made.
Do NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise cover all types of problems?
Yes, the NCERT Solutions cover all types of problems present in the Miscellaneous Exercise.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App