
Pascal's Principle Formula: In a fluid, the container walls experience static pressure exerted by the fluid, acting vertically on the container. External pressure applied to the fluid causes an uneven distribution of pressure throughout the fluid. This concept, known as Pascal's principle after the physicist Blaise Pascal, specifically applies to external pressure. It results in higher pressure at the bottom compared to the top within the fluid.
Pascal's principle states that the force per unit area characterizes the transmission of external pressure through a fluid. The formula representing this principle is expressed as:
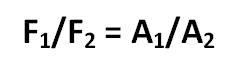
Pascal's Principle Formula Solved Examples
Example 1: Problem: In a hydraulic system, a force of 500 N is applied to a piston with a cross-sectional area of 20 square centimeters. The connected piston has a cross-sectional area of 80 square centimeters. Determine the force exerted on the second piston.
Solution: Given: Force on first piston (F 1 ) = 500 N Cross-sectional area of first piston (A 1 ) = 20 square centimeters Cross-sectional area of second piston (A 2 ) = 80 square centimeters
Using Pascal's principle formula: F 2 =A 2 ×F 1 /A 1
Substitute the known values:
F 2 =80×500/20
F 2 =2000N
The force exerted on the second piston is 2000 N.
Example 2: In a hydraulic jack, a small piston has a force of 300 N applied to it. The small piston has a cross-sectional area of 10 square centimeters. It's connected to a larger piston with a cross-sectional area of 50 square centimeters. Calculate the force exerted by the larger piston.
Solution: Given: Force on small piston (F 1 ) = 300 N Cross-sectional area of small piston (A 1 ) = 10 square centimeters Cross-sectional area of larger piston (A2) = 50 square centimeters
Using Pascal's principle formula: F 2 =A 2 ×F 1 /A 1
Substitute the known values: F 2 =50×300/10
F 2 =1500N The force exerted by the larger piston is 1500 N.
Example 3: In a hydraulic system, a piston with a force of 700 N is used on an area of 50 square centimeters. If this force is applied to a liquid connected to a second piston with an area of 200 square centimeters, find the force acting on the second piston.
Solution: Given: Force on first piston (F 1 ) = 700 N Cross-sectional area of first piston (A 1 ) = 50 square centimeters Cross-sectional area of second piston (A 2 ) = 200 square centimeters
Using Pascal's principle formula: F 2 =A 2 ×F 1 /A 1
Substitute the known values: F 2 =200×700/50
F 2 =2800N The force acting on the second piston is 2800 N.
Pascal's principle stands as a fundamental concept in fluid mechanics, particularly in hydraulic systems. It illustrates how external pressure applied to a confined fluid results in a uniform transmission of pressure in all directions within that fluid. As per the principle, the force per unit area remains constant throughout the fluid, allowing for the calculation of forces exerted on different pistons or surfaces based on their respective areas.
The Pascal's Principle Formula mathematical representation, F 2 = A 2/ A 1 ×F 1 , where F 2 is the force on the second piston, F 1 is the force on the first piston, A 2 is the area of the second piston, and A 1 is the area of the first piston, serves as a valuable tool in understanding and predicting the forces within hydraulic systems.
By leveraging the relationships between pressure, force, and the areas of pistons, one can accurately compute and predict the forces exerted on various components within these systems. This principle remains instrumental in diverse fields, from engineering and physics to everyday applications, providing a foundational understanding of fluid behavior and its applications in force transmission.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Physics knowledge. and build a strong foundation.
| Related Links | |
| Oscillatory Motion Formula | Resistivity Formula |
| Superposition Formula | Radio Waves Formula |
Pascal's Principle Formula FAQs
What is Pascal's Principle?
What is the formula for Pascal's Principle?
What does Pascal's Principle formula determine?
How is Pascal's Principle applied in everyday situations?
What happens if the area of the second piston is larger than the first?










