
Radians to Degrees Formula: Converting radians to degrees is a fundamental angle measurement transformation used in geometry. In angle measurement, two distinct systems are utilized: radians and degrees. Radians are primarily used in trigonometry. The process of converting angles from radians to degrees involves a specific formula. To grasp this conversion, it's important to comprehend the significance of each angle unit. Furthermore, this article will feature a conversion table detailing radians to degrees.
Converting Between Radians and Degrees
Two distinct units, radians and degrees, are used to measure angles. Consequently, mastering the conversion between these angle units, specifically from radians to degrees and degrees to radians, becomes crucial. As we rotate the radius of a circle, angles are formed, measurable in either radians or degrees. Understanding the significance of each angle unit and the process of measuring these angles becomes essential.
Radians
When the radius completes a full revolution around the circle, it encompasses 2π radians. The angular measure, in radians, formed at the circle's center by the radius is determined by the ratio of the arc's length to the radius. Once the arc's length equals the radius, the angle at the center becomes 1 radian. Represented as 'rad,' radians stand as the SI unit for measuring angles.
Degrees
Angle measurement in degrees involves dividing one complete revolution into 360 equal parts, with each part known as a degree. Upon a full rotation of the radius around the circle, it forms an angle of 360° at the center. Denoted by the symbol '°,' degrees aren't an SI unit for angle measurement but are widely accepted. It's often preferable to convert angles from radians to degrees for clearer understanding when problem-solving. The protractor serves as the tool for measuring angles in degrees.
Comparison of angle measures for a complete revolution reveals:
360 Degrees = 2π Radians
180 Degrees = π Radians
Converting Radians to Degrees Formula
The radians to degrees conversion formula is utilized to transform radians into degrees. To accomplish this conversion, radians are multiplied by 180°/π radians. Angle measurement uses two units: degrees, denoted as 1°, and radians, written as 1 (or) 1c; when no specific unit is provided, it implies measurement in radians. A complete circle is divided into 360 equal parts, known as degrees. A full counterclockwise rotation is equivalent to 2π in radians and 360° in degrees. Consequently, the measures of degrees and radians are interconnected. The conversion formula from Radians to Degrees Formula is expressed as:
Angle in Radians × 180°/π = Angle in Degrees
Derivation of the Radians to Degrees Formula
A full rotation around a circle amounts to 2π radians, which is equal to 360°. Thus, we have the relationship: 2π radians = 360°. To derive the formula for converting radians to degrees, we simplify this equation.
2π radians = 360°
Dividing both sides by 2, we get:
π radians = 360°/2
This simplifies to:
π radians = 180°
From this, we deduce that 1 radian equals 180° divided by π:
1 radian = 180°/π
Hence, the angle in degrees is obtained by multiplying the angle in radians by 180°/π. Hence, the formula for converting Radians to Degrees Formula is expressed as:
Angle in Radians × 180°/π = Angle in Degrees
Therefore, this process reveals the derivation of the radians to degrees formula.
Hence, for the conversion of radians to degrees, apply the formula = Radian measure × (180°/π). The resulting unit of measure will be in degrees (°). Specifically, 1 radian is equivalent to 57.296 degrees (°).
How to Convert Radians to Degrees
Radians and degrees serve as the two units for measuring angles. After a full circle revolution, 2π radians correspond to 360°. The conversion of radians to degrees can be executed using the formula 'Angle in Radians × 180°/π = Angle in Degrees'. To convert an angle provided in radians to degrees, follow these steps:
Record the angle measurement given in radians.
Since 1 radian equals 180°/π, multiply the given angle in radians by 180°/π to convert it into degrees.
Angle in Degrees = Angle in Radians × 180°/π
Simplify the values obtained and present the answer in degrees (°).
Let's illustrate this with an example.
Let's take an angle π / 6 radians. To convert this angle from radians to degrees using the conversion formula:
(π / 6) × (180°/π) = (Angle in Degrees)
By computation:
Angle in Degrees = 180°/6 = 30°
Therefore, π / 6 radians is equal to 30°.
Key Points for Radians to Degrees Conversion
These essential points should be noted for Radians to Degrees Formulas:
- Angle measurement utilizes two fundamental units: degrees and radians.
- A complete counterclockwise revolution equates to 2π radians.
- The conversion factors are: 1° = 0.017453 radians and 1 radian = 57.2958°.
- To convert an angle from radians to degrees, multiply it by 180°/π.
- For conversion from degrees to radians, multiply the angle by π/180°.
Table for Converting Radians to Degrees
Here, we compile the conversion of commonly used angles from radians to degrees, essential for problem-solving. The table provided below displays the radian values corresponding to specific angle measures in degrees:
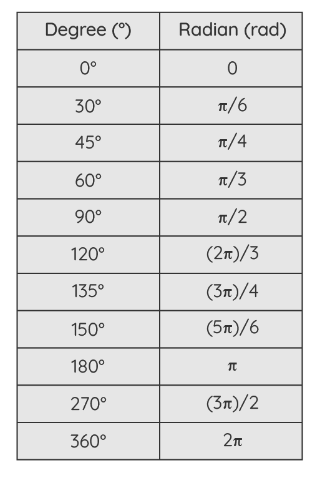
Chart for Radians to Degrees Conversion
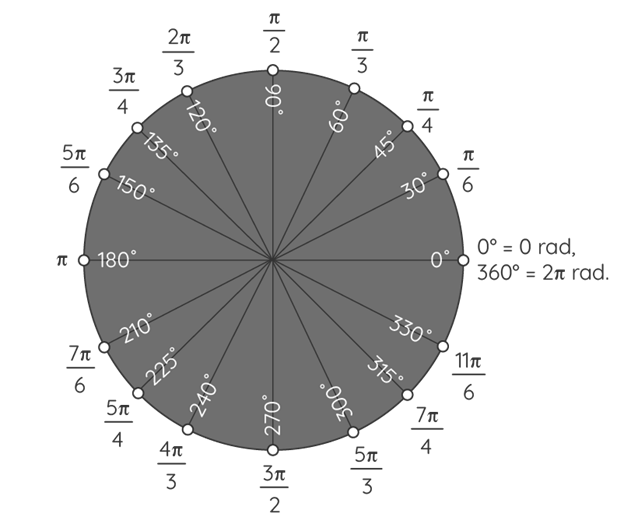
For a comprehensive reference, the following chart displays the correlation between angle measures in degrees and their corresponding measures in radians. In a unit circle, the circumference equals 2π, akin to a complete rotation of 360º, as depicted below.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Function Notation Formula | Hexagonal Pyramid Formula |
| Hypothesis Testing Formula | Interquartile Range Formula |
Radians to Degrees Formula FAQs
What are the units used to measure angles?
What does a complete counterclockwise rotation equate to in radians?
What is the conversion factor between degrees and radians?
How do you convert radians to degrees using a formula?
How do you convert degrees to radians using a formula?










