

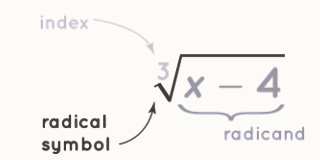
Radical Formulas , also known as roots, are mathematical operations that are essentially the reverse of exponentiation. They are represented by the radical symbol (√), and the number preceding the symbol is called the index or degree. The index specifies which root you are taking, such as a square root (index 2), cube root (index 3), fourth root (index 4), and so on. The index is a positive integer, and it denotes the degree of the root.
The general form of a radical is as follows:
√(x) = y
Here, 'x' is the radicand, which is the number or expression inside the radical, and 'y' is the result of taking the root of 'x' with the specified index.
Radicals can be used for both integers and real numbers, as well as expressions. When dealing with expressions inside radicals, you can simplify them by looking for factors that can be taken out of the root, which can make the calculations easier. For example:
√(16) = √(4 * 4) = 4
Here, you can see that you can simplify the square root of 16 by breaking it down into the square root of 4, which is 2.
It's important to note that there are rules for performing operations with radicals, such as addition, subtraction, multiplication, and division, which involve simplifying the expressions and rationalizing the denominators when necessary. These rules are important for solving more complex problems involving radicals.
Radical Definition
The symbol '√' used to represent a root of a number is indeed called a radical. It is typically read as "the nth root of x," and the horizontal line that covers the number is referred to as the vinculum. The number beneath the vinculum is known as the radicand, and the number 'n' written before the radical symbol is called the index or degree. For instance, when you see √7, it denotes the square root of 7, with 2 as the implied index.
Radicals can also be associated with the following terms:
Radical Equation: An equation that contains a radical expression is known as a radical equation. For example, an equation like √(x-3) = 5 is a radical equation.
Radical Expression: An expression that is enclosed within a radical symbol, such as √(2y+1), is called a radical expression. It represents a quantity that needs to be evaluated by taking the appropriate root.
Radical Inequality: An inequality that involves a radical expression is termed a radical inequality. For instance, an inequality like √x < 4 is a radical inequality, where the solution set involves values of 'x' that satisfy the inequality when the square root is taken.
Understanding radicals, their associated terms, and how to work with them is important in various mathematical contexts, including algebra and calculus.
What is Radical?
A radical in mathematics refers to the same concept as a root, encompassing different types of roots such as the square root, cube root, or nth root. The term "radical" is derived from the Latin word "Radix," which means "root." A radical essentially denotes the operation of finding a root of a number or expression. The number preceding the radical symbol is called the index number or degree, and it indicates how many times the number needs to be multiplied by itself to equal the radicand. In essence, this is the reverse of exponentiation, analogous to how addition is the opposite of subtraction and division is the opposite of multiplication.
For example, when we see ∛125, it means finding the cube root of 125, which is 5, because 5 × 5 × 5 equals 125. The index number, in this case, is 3, denoting that we're finding the cube root.
Radical Formula
To solve radical equations by eliminating the radical. Here's a breakdown of the steps you've outlined:
Start with the radical equation:
n√(x) = p
To make the equation radical-free, raise both sides to the power of 'n':
(n√x) n = p n
This eliminates the radical on the left side:
x = p n
In summary:
The symbol n√ is the radical of the nth root.
'n' is the index, representing the degree of the root.
The expression or variable inside the radical symbol (x) is known as the radicand.
Solving radical equations is a common mathematical operation and is often used in algebra and calculus. Your explanation provides a clear and straightforward approach to handling these equations.
The radical formula, as discussed earlier, is a fundamental concept in mathematics, and it has various practical applications in fields such as science, engineering, finance, and more. Here are some examples of how the radical formula can be applied in different contexts:
Geometry:
Calculating distances in three-dimensional space: In geometry, the distance between two points in 3D space can be calculated using the three-dimensional radical formula, which is an extension of the Pythagorean theorem for three dimensions.
Physics:
Kinematics: In physics, when calculating the displacement, velocity, or acceleration of an object undergoing motion, the radical formula is used to find distances, speeds, and other quantities. For example, calculating the magnitude of a vector in two- or three-dimensional motion.
Engineering:
Electrical engineering: In electrical circuits, the radical formula is used to find the impedance in complex AC circuit analysis.
Mechanical engineering: When analyzing mechanical vibrations, the radical formula can be applied to determine amplitudes, frequencies, and other characteristics.
Finance:
Compound interest: In finance, when calculating compound interest, the radical formula is used to determine the future value of an investment or loan.
Computer Science:
Algorithms: Algorithms for numerical methods and simulations often involve the manipulation of equations that contain radicals.
Chemistry:
Rate laws: In chemical kinetics, the radical formula is used to determine reaction rates and reaction orders.
Biology:
Growth models: In population biology and epidemiology, the radical formula is applied to model population growth and the spread of diseases.
Statistics:
Estimation of standard deviation: The sample standard deviation formula involves taking the square root of the variance, which is a common application of the radical formula in statistics.
Medicine:
Medical imaging: When analyzing medical images like MRI scans, the radical formula can be used in image reconstruction and analysis.
These are just a few examples of the many practical applications of the radical formula across different fields. Its versatility and usefulness make it a fundamental concept in mathematics and science.
Radical General Rules
The rules mentioned regarding radicals are indeed important for understanding how to work with them:
If the number under the radical is positive, the result will be positive.
√(25) = 5, as 25 is positive.
If the number under the radical is negative, the result will be negative.
√(-9) = -3, as -9 is negative.
If the number under the radical is negative and the index is an even number, the result will be an irrational number.
√(-4) is undefined in the real number system because taking the square root of a negative number with an even index results in an imaginary number.
If the index is not mentioned, the radical is assumed to be the square root.
Multiplication of numbers under the same radical and with the same index is possible.
∛12 × ∛10 = ∛(12 × 10) = ∛120.
Division is possible for numbers under the same radical.
√8/√4 = √(8/4) = √2.
The reverse of the multiplication rule is possible, where numbers are separated under the same radical.
√27 = √(9 × 3) = √9 × √3 = 3√3.
Radicals can be written in exponent form in equations.
√x = 25 can be rewritten as (√x) 2 = 25, which implies x = 25 2 .
The inverse exponent of the index number is equivalent to the radical itself.
√7 = 7 1/2 , which represents the square root of 7.
Understanding these rules is essential for simplifying expressions, solving equations, and working with radicals in various mathematical contexts.
Radical Formula Examples
Square Root:
Formula: √x
Example: √25 = 5
Explanation: The square root of 25 is 5 because 5 * 5 = 25.
Cube Root:
Formula: ∛x
Example: ∛8 = 2
Explanation: The cube root of 8 is 2 because 2 * 2 * 2 = 8.
Fourth Root:
Formula: ⁴√x
Example: ⁴√16 = 2
Explanation: The fourth root of 16 is 2 because 2 * 2 * 2 * 2 = 16.
nth Root:
Formula: n√x
Example: ³√27 = 3
Explanation: The third (cube) root of 27 is 3 because 3 * 3 * 3 = 27.
Application in Distance Calculation:
Formula: Distance = √((x2 - x1)² + (y2 - y1)²)
Example: To find the distance between two points, (3, 4) and (6, 8), you can use the formula:
Distance = √((6 - 3)² + (8 - 4)²) = √(3² + 4²) = √(9 + 16) = √25 = 5 units.
Compound Interest:
Formula: A = P(1 + r/n) nt
Example: To calculate the future value (A) of an investment with an initial principal (P) of $1,000, an annual interest rate (r) of 5%, compounded quarterly (n = 4) for 4 years (t), you can use the formula:
A = 1000(1 + 0.05/4)^(4*4) = 1000(1.0125)^16 ≈ $1216.65.
Standard Deviation:
Formula: σ = √[Σ(xi - μ)² / N]
Example: To calculate the standard deviation (σ) of a.
| Related Links | |
| Difference Quotient Formula | Probability |
| Effect Size Formula | Consecutive Integers Formula |
Radical Formula FAQs
Q1. What is a radical in mathematics?
Q2. What is the difference between the radicand and the index in a radical?
Q3. What happens if the radicand is negative and the index is even?
Q4. Can you simplify radicals?
Q5. What is the purpose of the radical formula in practical applications?












