Relativistic Doppler Effect Formula - Definition, Formula , Solved Examples
Relativistic Doppler Effect Formula : The Relativistic Doppler Effect is a fundamental concept in physics, helping us understand how the universe behaves at high speeds.
Murtaza Mushtaq11 Oct, 2023
Share
Relativistic Doppler Effect Formula : The Relativistic Doppler Effect is a relativistic correction to the classical Doppler Effect, which describes the change in frequency and wavelength of waves due to the relative motion of the source and observer. This effect comes into play when objects are moving at a substantial fraction of the speed of light.
The Relativistic Doppler Effect holds immense significance in modern physics and astrophysics. It accounts for the changes in frequency and wavelength of electromagnetic waves when objects move at significant fractions of the speed of light. This phenomenon is fundamental in understanding the behavior of light from distant cosmic objects, such as galaxies and stars, as they move relative to observers on Earth. The Relativistic Doppler Effect plays a critical role in confirming the expanding universe theory, enabling us to measure cosmic velocities and infer crucial information about the cosmos. Its applications also extend to technologies like GPS, where it corrects for satellite motion at high speeds, making it an indispensable tool in both theoretical and practical aspects of physics and navigation.Formula Of Relativistic Doppler Effect
The formula for the Relativistic Doppler Effect can be expressed as follows: f' = f * sqrt((1 + β) / (1 - β))Where:
- `f'` is the observed frequency. - `f` is the source frequency. - `β` is the ratio of the relative velocity to the speed of light.Alternatively
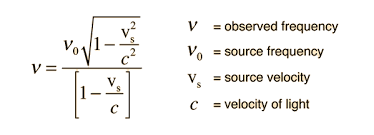
Also Check - Soil Erosion Formula
Solved Problems Of Relativistic Doppler Effect Formula :
Solved Problem 1: A spaceship is moving at 0.95c, and it detects a gamma-ray burst with a known frequency of 10^20 Hz. What is the observed frequency on the spaceship?Solution:
Using the Relativistic Doppler Effect formula, we calculate the observed frequency as follows: f' = f * sqrt((1 + β) / (1 - β)) f' = 10^20 Hz * sqrt((1 + 0.95) / (1 - 0.95)) f' ≈ 3.74 x 10^20 Hz So, the observed frequency on the spaceship is approximately 3.74 x 10^20 Hz.Also Check - Photon Energy Formula
Solved Problem 2: A galaxy is moving away from Earth at 0.7c, and it emits light with a wavelength of 500 nm. What is the observed wavelength on Earth?Solution:
Using the Relativistic Doppler Effect formula for wavelength, we have: λ' = λ * sqrt((1 - β) / (1 + β)) λ' = 500 nm * sqrt((1 - 0.7) / (1 + 0.7)) λ' ≈ 195.48 nm So, the observed wavelength on Earth is approximately 195.48 nm.Also Check - Shear Modulus Formula
Solved Problem 3: A rocket is moving towards a star at 0.6c, and the star emits radio waves at 1 GHz. What is the observed frequency on the rocket?Solution:
Using the formula, we can calculate the observed frequency: f' = f * sqrt((1 + β) / (1 - β)) f' = 1 GHz * sqrt((1 + 0.6) / (1 - 0.6)) f' ≈ 2.5 GHz The observed frequency on the rocket is approximately 2.5 GHz.Also Check - Efficiency Formula
Solved Problem 6:
An astronaut on a spaceship moving at 0.8c observes a laser emitting light at 600 nm. What is the observed wavelength?Solution:
Applying the Relativistic Doppler Effect formula for wavelength, we get: λ' = λ * sqrt((1 - β) / (1 + β)) λ' = 600 nm * sqrt((1 - 0.8) / (1 + 0.8)) λ' ≈ 194.38 nm The observed wavelength on the spaceship is approximately 194.38 nm. Solved Problem 4: A distant galaxy is receding from Earth at 0.9c, and it emits visible light with a wavelength of 550 nm. What is the observed wavelength on Earth? Solution: Using the formula for wavelength, we can find the observed wavelength: λ' = λ * sqrt((1 - β) / (1 + β)) λ' = 550 nm * sqrt((1 - 0.9) / (1 + 0.9)) λ' ≈ 99.50 nm The observed wavelength on Earth is approximately 99.50 nm. These solved problems illustrate the application of the Relativistic Doppler Effect formula in different scenarios, showcasing its importance in understanding how waves are affected by relative motion. The Relativistic Doppler Effect is a fundamental concept in physics, helping us understand how the universe behaves at high speeds. It provides insights into the fascinating world of relativistic corrections to wave phenomena and plays a vital role in astrophysics and other scientific fields.The Relativistic Doppler Effect plays a critical role in confirming the expanding universe theory, enabling us to measure cosmic velocities and infer crucial information about the cosmos.Relativistic Doppler Effect Formula FAQs
What is the classical Doppler Effect?
The classical Doppler Effect describes the change in frequency or wavelength of waves due to relative motion, typically at much lower speeds than the speed of light.
Why is it called the 'Relativistic' Doppler Effect?
It's named 'relativistic' because it accounts for relativistic effects, considering objects moving at significant fractions of the speed of light.
How does the Relativistic Doppler Effect affect space observations?
It's crucial for astrophysicists as it explains the observed shifts in the spectra of distant galaxies and their motion.
Can the Relativistic Doppler Effect be applied to sound waves?
No, it's specific to electromagnetic waves, like light. Sound waves operate differently.
Can the Relativistic Doppler Effect be observed in everyday life?
Not in everyday scenarios, as the speeds involved are usually negligible compared to the speed of light.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.