
Trigonometric Ratios and Their Origins
In trigonometry, sine (sin), cosine (cos), and tangent (tan) are the basic trigonometric ratios used to analyze the relationships between the angles and sides of a triangle, particularly in right-angled triangles.
The study of these ratios has a rich historical background. Pythagoras introduced the Pythagorean theorem to establish a relationship between the sides of a right triangle. Later, Hipparchus contributed to the development of trigonometry by establishing relationships between the sides and angles of right triangles using these concepts.
What is Sin Cos Tan Formula in Trigonometry?
The definitions of the "opposite side" and "adjacent side" in a right-angled triangle within the context of trigonometry:
In trigonometry, we use three primary trigonometric ratios: sine (sin), cosine (cos), and tangent (tan). These ratios relate to the sides of a right-angled triangle. In a right-angled triangle, the longest side is always called the "hypotenuse," while the other two sides are named based on the angle we are considering.
Opposite Side (Perpendicular):
The "opposite side" is the side of the triangle that is directly "opposite" to the angle under consideration. It is the side that does not touch or include the angle itself. It is the side that forms a right angle with the hypotenuse.
Adjacent Side (Base):
The "adjacent side," also known as the "base," is the side of the triangle (other than the hypotenuse) that "touches" or is adjacent to the angle. It is the side that is not the hypotenuse and is connected to the angle without being opposite to it.
These definitions help us precisely identify and work with the sides of a right-angled triangle in trigonometry. The choice of "opposite" and "adjacent" sides depends on the specific angle being considered and is essential for applying trigonometric functions effectively.
Sin Cos Tan Values
Sin, Cos, and Tan values in trigonometry represent the values of the corresponding trigonometric functions for a given angle. These values can be determined by calculating the ratios of the sides in a right triangle. Let's delve into the detailed formulas to compute these ratios in the following sections.
Sin Cos Tan Formula
In trigonometry, the sine (sin), cosine (cos), and tangent (tan) functions are defined in relation to the sides of a right-angled triangle. Specifically, they are based on the relationships between two of the three sides: the opposite side, the adjacent side, and the hypotenuse. These functions are denoted as follows:
Sine (sin θ): It is the ratio of the length of the side opposite to the angle θ to the length of the hypotenuse.
Mathematically, sin θ = Opposite/Hypotenuse.
Cosine (cos θ): It is the ratio of the length of the side adjacent to the angle θ to the length of the hypotenuse.
Mathematically, cos θ = Adjacent/Hypotenuse.
Tangent (tan θ): It is the ratio of the length of the side opposite to the angle θ to the length of the side adjacent to the angle θ.
Mathematically, tan θ = Opposite/Adjacent.
Additionally, there are reciprocal trigonometric ratios known as cosecant (csc), secant (sec), and cotangent (cot), which are the reciprocals of sin, cos, and tan, respectively.
Example: To find the sin, cos, and tan of a given angle θ in a right triangle, follow these steps:
Identify the sides of the triangle. The hypotenuse is the longest side, the side opposite θ is the opposite side (or perpendicular), and the side adjacent to θ is the adjacent side (or base).
Use the Formulas for Sin Cos and Tan
sin θ = Opposite/Hypotenuse
cos θ = Adjacent/Hypotenuse
tan θ = Opposite/Adjacent
For example, if sin θ = 3/5, cos θ = 4/5, and tan θ = 3/4, these ratios represent the relationships between the sides of the triangle for the given angle θ.
Applications of Sin Cos and Tan Formulas
Sin, cos, and tan formulas in trigonometry are powerful tools for solving various problems involving right-angled triangles. These formulas are used to find missing sides or angles, making them essential in various fields, including physics, engineering, surveying, and navigation.
Overall, your explanation provides a solid foundation for understanding the importance of sine, cosine, and tangent in trigonometry and their practical applications.
Trick to Remember Sin Cos and Tan Formulas
A helpful mnemonic to remember the trigonometric ratios and their corresponding formulas is "SOHCAHTOA":
S for "Sine" (sin), which represents "Opposite/Hypotenuse."
O for "Cosine" (cos), which represents "Adjacent/Hypotenuse."
H for "Hypotenuse."
C for "Cosine" (cos).
A for "Adjacent."
T for "Tangent" (tan), which represents "Opposite/Adjacent."
This acronym can serve as a handy memory aid to recall the relationships between the sides of a right-angled triangle and the trigonometric functions.
Sin Cos Tan Table
The trigonometric ratios, sine (sin), cosine (cos), and tangent (tan), are primarily based on the angles of a triangle, and they represent the relationships between the sides of a right-angled triangle, not the side lengths themselves. These ratios are dimensionless and depend solely on the given angle. A trigonometric table or chart is a valuable tool for quickly finding the values of these functions for standard angles, making calculations more efficient and convenient.
These tables provide a reference for the sine, cosine, and tangent values at common angles, such as 0°, 30°, 45°, 60°, and 90°. They simplify trigonometric calculations by allowing users to look up values rather than performing complex calculations for these standard angles. This is especially useful in various fields, including mathematics, physics, engineering, and more, where trigonometric functions play a crucial role in problem-solving and analysis.
In summary, trigonometric ratios are angle-dependent, and trigonometric tables or charts provide a quick reference for their values at standard angles, streamlining mathematical and scientific computations.
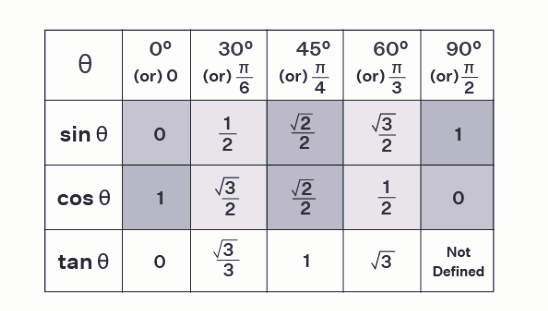
Tips to Remember Sin Cos Tan Table
Tips for memorizing and understanding the values in the trigonometric table are spot on and can be quite helpful for students and anyone dealing with trigonometry. Here's a summary of the key points you've highlighted:
Memorize the Key Angles: Focus on memorizing the angles 0°, 30°, 45°, 60°, and 90°. These are the most commonly used angles in trigonometry.
Remember the First Row of Sin Values: Recall the first row of sine (sin) values using the sequence 0/2, √1/2, √2/2, √3/2. These values correspond to the angles 0°, 30°, 45°, and 60°, respectively.
Understand the Symmetry: Note that the row of cosine (cos) values is identical to the row of sine values but in reverse order. This symmetry simplifies memorization.
Use the Relationship Between Sin and Cos for Tan: Understand that the tangent (tan) of an angle is calculated by dividing the corresponding sine value by the cosine value, as tan(θ) = sin(θ)/cos(θ). This relationship allows you to find tan values based on sin and cos.
By following these tips, you can quickly reference and work with trigonometric values for common angles, making trigonometry calculations more manageable and efficient.
Application of Sin Cos Tan in Real Life
Trigonometric ratios such as sine (sin), cosine (cos), and tangent (tan) find wide-ranging applications in solving real-life problems related to heights and distances. They are valuable tools for measuring and calculating various physical quantities. Let's illustrate their practical application with an example
Example: Determining the Height Reached by a Ladder
Imagine a scenario where a ladder is leaning against a brick wall, forming an angle of 50 degrees with the horizontal. You want to find out how high the ladder reaches on the wall when it is placed 10 feet away from the wall.
Solution:
Let's assume that the ladder reaches a height of x feet on the wall. To solve this problem, we can apply trigonometric principles:
Identify the known values: In this case, the ladder's distance from the wall is the adjacent side, which is 10 feet, and we want to find the height, which is the opposite side.
Utilize the appropriate trigonometric ratio: Since we are given the adjacent side and want to find the opposite side, we can use the tangent (tan) function. The relationship is expressed as:
tan(50°) = x / 10
Solve for x: To find the height, we can rearrange the equation:
x = 10 * tan(50°)
Calculate the height: Using a calculator, we evaluate tan(50°) and obtain an approximate value.
x ≈ 11.9 feet
Therefore, the ladder reaches a height of approximately 11.9 feet on the wall.
This example demonstrates how trigonometric ratios, specifically the tangent function, are applied to real-life situations to solve problems related to heights and distances, making them valuable tools in various fields, including construction, engineering, and surveying.
| Related Links | |
| Line and Angles Formula | Line and Angles Formula |
| Exponential Formula | Factorial Formula |
Sin Cos Tan Formula FAQs
Q1. What is the sine (sin) function in trigonometry?
Q2. What is the tangent (tan) function in trigonometry?
Q3. What is the formula for the sine (sin) function?
Q4. What is the formula for the tangent (tan) function?










