Strain Formula:
Strain, in the context of materials, refers to the deformation that occurs when an object or material experiences an external force. This deformation can be a change in shape, size, or both. Imagine stretching a rubber band or compressing a spring; these actions result in strain, and it's the measurement of this strain that allows engineers and scientists to understand how materials behave under different conditions.
Strain Formula and Derivation
To precisely quantify strain, we use a formula. The formula for strain
(ε)
is relatively straightforward:
Strain (ε) = Change in Length (ΔL) / Original Length (L)
This formula tells us the fractional or percentage change in the material's length due to the applied force. The derivation of this formula involves principles from geometry and mechanics, where we consider the change in length compared to the original length of the material.
Types of Strain
Strain Formula: Strain isn't a one-size-fits-all concept. There are several types of strain, each catering to specific situations. The most common types include:
-
Normal Strain:
- Occurs due to the application of normal (perpendicular) forces.
- Results in changes in length or dimensions.
-
Shear Strain:
- Occurs when forces act parallel to the material's surface.
- Results in changes in the material's shape without affecting its volume.
-
Volumetric Strain:
- Involves changes in the volume of the material.
- Often relevant in fluid mechanics and geology.
Each type of strain has unique characteristics and applications, making it essential to understand them in-depth.
Also Check -
Relativistic Doppler Effect Formula
Stress-Strain Curve
Strain Formula: The relationship between stress and strain is a fundamental concept in materials science and engineering. It's often visualized through a stress-strain curve, which illustrates how a material responds to external forces. The curve helps in determining key material properties, such as elasticity, yield strength, and toughness.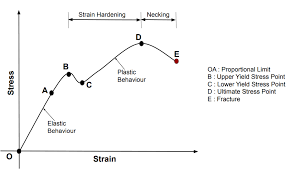
Also Check -
Heat Input Formula
Things to Remember
In practical applications, understanding strain is crucial for engineers and scientists. Here are some key takeaways:
- Strain is a measure of deformation due to an applied force.
- It can be categorized into normal strain, shear strain, and volumetric strain.
- Stress-strain curves help us understand a material's mechanical behavior.
Also Check -
Cell Potential Formula
Sample Questions Solved Of Strain Formula
-
Example 1: Calculating Normal Strain
- A steel rod with an original length of 2 meters is subjected to a tensile force, resulting in a 0.02-meter elongation. Calculate the normal strain.
Solution:
Using the formula for strain:
Strain (ε) = Change in Length (ΔL) / Original Length (L)
Strain (ε) = (0.02 m) / (2 m) = 0.01
The normal strain is 0.01, or 1%
.
-
Example 2: Stress-Strain Curve Analysis
-
A stress-strain curve for a material exhibits a linear region with a slope of 300 MPa. What does this slope represent, and what can you deduce about the material's behavior?
Solution:
The slope of a stress-strain curve in the linear region represents Young's Modulus (E), which measures a material's stiffness. In this case, the material has a Young's Modulus of 300 MPa. This indicates that the material is quite stiff and has a high resistance to deformation in the elastic range.
-
Example 3: Shear Strain Calculation
-
A rectangular block experiences a shearing force, resulting in a 0.03-meter deformation along one of its sides while maintaining its original shape in other dimensions. Calculate the shear strain.
Also Check -
Normal Force Formula
Solution:
Shear strain (γ) = Change in position (Δx) / Original position (x)
Shear strain (γ) = (0.03 m) / (Original side length) = (0.03 m) / (Original side length)
-
Example 4: Volumetric Strain in a Liquid
- A container holding 500 mL of water is subjected to increased pressure, causing the water to compress to 480 mL. Calculate the volumetric strain.
Solution:
Volumetric strain (ε_v) = Change in volume (ΔV) / Original volume (V)
Volumetric strain (ε_v) = (480 mL - 500 mL) / 500 mL = -0.04 or -4%
The negative sign indicates compression.
-
Example 5: Combined Normal and Shear Strain
- A block of material is subjected to both normal and shear forces. It experiences a normal strain of 0.02 and a shear strain of 0.01. Calculate the total strain.
Solution:
The total strain
(ε_total)
is the vector sum of the normal and shear strains.
ε_total = √(normal strain² + shear strain²)
ε_total = √(0.02² + 0.01²) = √(0.0004 + 0.0001) = √0.0005
ε_total ≈ 0.0224 or 2.24%
These solved examples demonstrate the application of strain concepts and the use of strain formulas. They provide practical insights into how strain calculations are used in various scenarios, from simple elongation to complex deformation in different materials.
Strain is an essential concept in materials science and engineering, offering insights into how materials respond to forces and deformations. This comprehensive guide has introduced you to the fundamentals of strain, its types, the strain formula, and its derivation. By understanding strain, you gain the knowledge needed to design, analyze, and work with materials effectively, whether in civil engineering, mechanical engineering, or other fields where materials play a critical role.
Now, equipped with the knowledge of strain, you can confidently approach various applications and challenges, ensuring the safety and integrity of structures and components.
