
CBSE Class 12 Maths Notes Chapter 9: CBSE Class 12 Maths Notes Chapter 9 Differential Equations, which are equations involving function derivatives. It introduces the concept of order and degree of a differential equation. The chapter covers methods to form differential equations, solve first-order and first-degree differential equations using techniques like separation of variables, and homogeneous, and linear differential equations.
It also explains how differential equations are applied in real-life situations, such as population growth, radioactive decay, and cooling laws. Understanding these concepts is essential for solving problems related to physics, economics, and other scientific fields.CBSE Class 12 Maths Notes Chapter 9 Overview
CBSE Class 12 Maths Notes Chapter 9 Differential Equation, delves into one of the most important concepts in calculus. A differential equation is a mathematical equation that involves an unknown function and its derivatives. The chapter begins with an introduction to the order and degree of a differential equation, which represent the highest derivative and the power of the highest derivative, respectively, in the equation. The chapter proceeds to explain the formation of differential equations by eliminating arbitrary constants from given functions. Several methods of solving first-order and first-degree differential equations are introduced, including separation of variables, homogeneous equations, and linear differential equations. Each method has specific conditions under which it is applied, and the chapter provides a systematic approach to choosing the appropriate solution technique. The chapter also emphasizes the application of differential equations in modeling various real-world phenomena, such as population growth, the cooling of objects, radioactive decay, and motion under gravity. These practical applications highlight the importance of understanding how differential equations can describe natural processes and predict future behaviors.CBSE Class 12 Maths Notes Chapter 9 PDF
Here we have provided CBSE Class 12 Maths Notes Chapter 9 Differential Equation pdf for the ease of the students so that they can download this pdf for access it offline.CBSE Class 12 Maths Notes Chapter 9 PDF
CBSE Class 12 Maths Notes Chapter 9 Differential Equation
Here we have provided CBSE Class 12 Maths Notes Chapter 9 Differential Equation -What are differential equations?
Differential equations are those that involve the derivative of the dependent variable with respect to the independent variable. The highest order of the occurring derivative is assigned here. The degree of the polynomial equation's appearance in the derivatives is indicated.dy/dx = f(x)
Here “x” is an independent variable and “y” is a dependent variable For example, dy/dx = 5xOrder of Differential Equation
The highest order derivative included in the differential equation determines its order. Here are a few instances of the differential equation for various orders.- dy/dx = 3x + 2 , The order of the equation is 1
- (d 2 y/dx 2 )+ 2 (dy/dx)+y = 0. The order is 2
- (dy/dt)+y = kt. The order is 1
Degree of Differential Equation
When the original equation is expressed as a polynomial equation with derivatives like y', y", y"', and so forth, the degree of the differential equation is equal to the power of the highest order derivative. Suppose (d 2 y/dx 2 )+ 2 (dy/dx)+y = 0 is a differential equation, so the degree of this equation here is 1. See some more examples here:- dy/dx + 1 = 0, degree is 1
- (y”’) 3 + 3y” + 6y’ – 12 = 0, degree is 3
- (dy/dx) + cos(dy/dx) = 0; it is not a polynomial equation in y′ and the degree of such a differential equation can not be defined.
Types of Differential Equations
Differential equations can be divided into several types namely- Ordinary Differential Equations
- Partial Differential Equations
- Linear Differential Equations
- Nonlinear differential equations
- Homogeneous Differential Equations
- Nonhomogeneous Differential Equations
Differential Equation formula

Order of Differential Equation
Differential equations are categorised according to their order. A differential equation's order is determined by the highest derivative, sometimes referred to as the differential coefficient, that is included in the equation.Example (i):
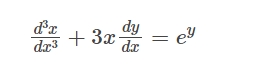
Example (ii):
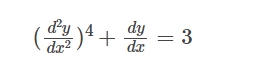
Example Problems
Question 1: Determine the order and degree for y’ + 5y = 0
Solution: Given, differential equation y’ + 5y = 0 Order = 1 (Highest order derivative is y’) Degree = 1 (Highest power raised to y’)Question 2: Determine the order and degree of y’’’ + 2y’’ + y’ = 0.
Solution: The given differential equation is, y’’’ + 2y’’ + y’ = 0 Order = 3 (Highest order derivative is y”’) Degree = 1 (Highest power raised to y”’)Question 3: Verify that the y = cos x + C is a solution of y′ + sin x = 0.
Solution: Given, y = cos x + C Differentiating both sides with respect to x, we get, y’ = d/dx(cos x + C) y’ = -Sin x Substituting the values of y’ in the given differential equations, y′ + sin x = 0, we get; = y’ + sin x = – sin x + sin x = 0 Therefore, y = cos x + C is a solution of y′ + sin x = 0.Applications of Differential Equations
We can describe the differential equations applications in real life in terms of:- Exponential Growth
G(t)= G 0 e kt
Let G 0 is positive and k is constant, then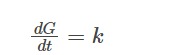
- Exponential reduction or decay
R(t) = R 0 e -kt
When R 0 is positive and k is constant, R(t) is decreasing with time,Benefits of CBSE Class 12 Maths Notes Chapter 9
The CBSE Class 12 Maths Notes on Chapter 9: Differential Equations offer several benefits for students:Concept Clarity : The notes simplify complex concepts like order, degree, and types of differential equations, making it easier to understand and retain the subject matter.
Efficient Revision : Concise summaries help students quickly revise key points and formulas, saving time during exam preparation.
Step-by-Step Solutions : The notes provide detailed methods for solving first-order and first-degree differential equations, guiding students through separation of variables, homogeneous equations, and linear differential equations.
Application Focused : Real-life applications like population growth, cooling, and radioactive decay help students grasp the practical importance of differential equations.
Exam-Oriented : The notes highlight important questions and problem-solving techniques, aiding students in tackling both conceptual and numerical problems effectively during exams.
CBSE Class 12 Maths Notes Chapter 9 FAQs
Who invented differential equations?
What is the purpose of the differential equation?
How are differential equations used in real life?
What is the main formula of a differential equation?










