CBSE Class 12 Maths Notes Chapter 7 Integrals PDF Download
Here we have provided CBSE Class 12 Maths Notes Chapter 7 Integrals for the ease of the students so that they can prepare better for their exams.
Neha Tanna9 Sept, 2024
Share
CBSE Class 12 Maths Notes Chapter 7: CBSE Class 12 Maths Notes Chapter 7 focuses on Integrals , a key concept in calculus. It explores the antiderivatives and indefinite integrals, along with integration as the reverse differentiation process. The chapter introduces various integration techniques, including integration by substitution, parts, and partial fractions.
It also covers the concept of definite integrals, properties of definite integrals, and the application of integrals in finding the area under curves. This chapter builds a strong foundation for solving real-world problems involving rates of change and accumulation, essential for higher studies in mathematics.CBSE Class 12 Maths Notes Chapter 7 Integrals Overview
CBSE Class 12 Maths Notes Chapter 7, is an essential part of calculus that deals with finding the antiderivatives or the inverse process of differentiation. Integrals play a crucial role in both pure and applied mathematics, especially when calculating areas, volumes, and various other quantities.
CBSE Class 12 Maths Notes Chapter 7 PDF
This chapter lays a strong foundation for understanding advanced topics in calculus and is crucial for students pursuing fields like engineering, physics, and economics. Hence, here we have provided CBSE Class 12 Maths Notes Chapter 7 Integrals pdf -CBSE Class 12 Maths Notes Chapter 7 PDF
CBSE Class 12 Maths Notes Chapter 7 Integrals
Here we have provided CBSE Class 12 Maths Notes Chapter 7 -
We already know that the derivative of a function f(x) exists at every point on an interval I if the function is differentiable on that interval. The challenge now becomes: can we obtain the function given the derivative of the function? Yes, is the response to this query. The original function can be obtained through integration, often known as the antiderivative of a function. Integration as an Inverse Process of Differentiation The term "inverse process of differentiation" refers to integration. We are asked to discover a function's primitive, or the original function, given its derivative rather than differentiating it. This kind of procedure is known as anti-differentiation or integration.Antiderivative Functions
Let us have a look at various antiderivative of functions.
Integral Types
The integral calculus is of the two forms, namely(i) Indefinite Integral
(ii) Definite Integral
A constant number "c" follows the value of the function obtained in an indefinite integral because the function's range is not defined. In contrast, a definite integral provides a well-defined function because the function's range is well-defined. The integration's symbol is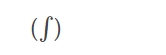
Indefinite Integrals
Some of the important concepts of indefinite integrals are as follows: Finding a function's antiderivatives is the process of integration in calculus. Put differently, integration might be thought of as the opposite of differentiation. We will obtain the arbitrary constant C through the process of function integration. The integrals we obtain will vary depending on the value of C. However, geometrically, those integrals are comparable. Here, we'll go into further detail and provide an example on the geometric interpretation of the indefinite integral.Geometrical Interpretation of Indefinite Integral Example
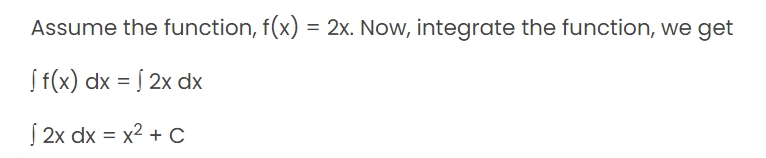Where C is called the arbitrary function, which represents the family of integrals.
We are aware that the integral values we obtain vary depending on the value of C. However, their integral values are comparable geometrically. This indicates that we can obtain the many family members that make up the indefinite integral by giving the arbitrary constant different values. As a result, the parabola with its axis along the y-axis is represented by each integral.
Methods of Integration
There are several ways to find the integral of a function in calculus, or to do integration. These techniques are applied to complicated function antiderivatives. They are as follows: Aside from differentiation, integration is a procedure covered in calculus that allows us to find the integrals of functions. One way to solve integrals is by integration by substitution. Another name for this technique is u-substitution. Here you can also discover integrals of certain functions.
We know the anti-derivatives of fundamental functions. These functions' integrals are easily obtained. However, this integration method is only applicable to fundamental functions; other integration techniques are needed to find the integrals of other functions. Let's talk about integration by substitution among various integration techniques.
Integration By Substitution Method
By replacing the independent variable with another, every given integral can be simplified using this integration procedure.
What is a Partial Fraction?
"Partial fractions" are the smaller units from which an algebraic fraction can be decomposed. Take the fraction (3x+5)/(2x2-5x-3) as an example in algebra. One can simplify this statement by splitting it into the form [2/(x – 3)] [1/(2x + 1)]. Partial fractions are the simpler components [1/(2x + 1)] and [2/(x – 3)]. As a result, the algebraic statement can be expressed in the format shown in the figure:Integration By Parts Formula
A unique method of integrating two functions after they are multiplied is called integration by parts. Partial integration is another name for this technique. The integration by replacement approach is an additional way to integrate a given function. Complicated integrations are made simple with the help of these techniques. Integrating a product of two functions by parts can be expressed mathematically as follows:∫f(x).g(x)dx=f(x)∫g(x)dx−∫f′(x).(∫g(x)dx)dx
Integration using Trigonometric Identities
The study of differentiation, which includes determining a function's derivative, is the focus of differential calculus. On the other hand, integral calculus is concerned with determining the integral values, which entails determining the function's antiderivative. To put it another way, differentiation is the process that integration is the opposite of.Integrals of Particular Function
The large-scale function summation technique is called an integral. Therefore, the integrals of a few specific functions that are frequently employed in calculations have been covered here. Numerous real-world uses of these integrals include determining the area between curves, volume, average function value, kinetic energy, centre of mass, work-done, and so forth.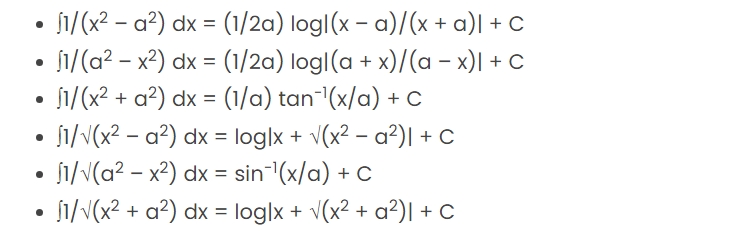
Definite Integral
Here,
∫ = Integration symbol
a = Lower limit
b = Upper limit
f(x) = Integrand
dx = Integrating agent
Thus, ∫
a
b
f(x) dx is read as the definite integral of f(x) with respect to dx from a to b.
Fundamental Theorem of Calculus
A theorem that connects the ideas of differentiating and integrating functions is known as the fundamental theorem of calculus. By calculating the difference between the antiderivative at the higher and lower bounds of the integration process, the calculus fundamental theorem validates the process. Let's go over the first and second fundamental theorems of calculus, along with how to use them to evaluate the definite integral.First Fundamental Theorem of Integral Calculus (Part 1)
The initial component of the calculus theorem is occasionally referred to as the calculus first fundamental theorem. It states that one of a function f's antiderivatives, or what is also referred to as an indefinite integral, let's say F, can be found as the integral of f with a variable integration bound. This indicates that a continuous function may have antiderivatives. Statement: Let f be a continuous function on the closed interval [a, b] and let A(x) be the area function. Then A′(x) = f(x), for all x ∈ [a, b]. Or Let f be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], by:
F(x)=∫axf(t)dt
Then F is uniformly continuous on [a, b] and differentiable on the open interval (a, b), and
F'(x) = f(x) ∀ x ∈(a, b)
Here, the F'(x) is a derivative function of F(x).
Second Fundamental Theorem of Integral Calculus (Part 2)
According to the second fundamental theorem of calculus, the following holds true if the function "f" is continuous on the closed interval [a, b] and F is an indefinite integral of a function "f" on [a, b]:F(b)- F(a) = a ∫ b f(x) dx
Here R.H.S. of the equation indicates the integral of f(x) with respect to x. f(x) is the integrand. dx is the integrating agent. ‘a’ indicates the upper limit of the integral and ‘b’ indicates a lower limit of the integral. A definite integral's function has a distinct value. One way to think about a function's definite integral is as a sum's limit. The difference between the values of F, or F(b) – F(a), is the definite integral of the function if there is an antiderivative F of the function in the interval [a, b].Remarks on the Second Fundamental Theorem of Calculus
- The equation ∑ab f(x) dx = (value of the antiderivative F of “f” at the upper limit b) - (the same antiderivative value at the lower limit a) is the second half of the calculus fundamental theorem.
- This theorem is particularly helpful since it gives us a way to estimate the definite integral faster without having to figure out the limit of the sum.
- The fundamental step in estimating a definite integral is determining a function whose derivative equals the integrand. On the other hand, this procedure will strengthen the connection between integration and differentiation.
- The function f(x), or simply "f," in the expression ∫ab f(x) dx, needs to be well-defined and continuous in the interval [a, b].
Benefits of CBSE Class 12 Maths Notes Chapter 7
The benefits of studying Chapter 7 Integrals from CBSE Class 12 Maths are vast, particularly for students looking to strengthen their calculus foundation. Some of the key advantages include:Foundation for Advanced Calculus : Understanding integrals is essential for higher-level calculus topics, such as differential equations and multivariable calculus.
Problem-Solving Skills : The techniques of integration, including substitution, by parts, and partial fractions, enhance a student's ability to solve complex mathematical problems.
Real-Life Applications : Integrals are used in various real-life scenarios, such as calculating areas under curves, solving physics problems related to motion and energy, and determining volumes of solids.
Understanding Definite Integrals : Mastering definite integrals helps students calculate precise areas and values, which are widely applied in economics, engineering, and sciences.
Preparation for Competitive Exams : A strong grasp of integrals is essential for success in competitive exams like JEE, NEET, and other entrance exams that involve mathematics.
Development of Analytical Thinking : Studying integrals nurtures logical and analytical thinking, as students learn to approach problems methodically.
CBSE Class 12 Maths Notes Chapter 7 FAQs
Is integral class 12 hard?
The difficulty of class 12th integrals lies in the level of your practice.
What is the easiest method of integration?
Integration by parts is also known as the product rule of integration and the UV method of integration. When you have to integrate rational functions, a method of integration using partial fractions is used. The reverse chain rule is also one of the easiest and most commonly used methods of integration.
What is the main rule of integration?
Integration rules are the rules used to integrate a function. The most important integration rules are as follows: ∫ xn dx = xn+1/(n+1) + C. ∫ ex dx = ex + C.
Can you integrate multiple times?
Many functions that can be integrated using integration by parts require that integration by parts be applied multiple times.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.