CBSE Class 12 Maths Notes Chapter 4 Determinants PDF Download
Ananya Gupta11 Sept, 2024
Share
CBSE Class 12 Maths Notes Chapter 4: CBSE Class 12 Maths Notes for Chapter 4 Determinants provide a detailed understanding of the topic which is important for students preparing for board exams. This chapter covers the concept of determinants, properties of determinants, and their application in solving linear equations, finding the area of triangles, and evaluating inverse matrices.
The notes simplify complex topics like minors, cofactors, and the adjoint of matrices, making them easier to grasp. By focusing on key formulas and step-by-step solutions these notes help students build a strong foundation and score well in their exams.CBSE Class 12 Maths Notes Chapter 4 Determinants Overview
CBSE Class 12 Maths Notes Chapter 4 Determinants is a fundamental topic in linear algebra that plays a significant role in solving systems of linear equations, finding areas of triangles, and more. Determinants are especially useful when dealing with matrices and have wide applications in both pure and applied mathematics. The chapter begins by introducing the concept of a determinant for a square matrix and explains how to calculate it using minors and cofactors. Important properties of determinants, such as linearity, the effect of row and column operations, and the determinant of a product of matrices, are discussed in detail. These properties allow students to simplify complex determinant calculations.CBSE Class 12 Maths Notes Chapter 4 PDF
The PDF link for CBSE Class 12 Maths Notes Chapter 4 Determinants is available below. These notes provide a detailed explanation of all the key concepts, properties and applications of determinants, helping students to grasp the material more effectively. You can download the PDF for easy access and revision anytime ensuring a thorough understanding of the chapter's contents.CBSE Class 12 Maths Notes Chapter 4 Determinants PDF
CBSE Class 12 Maths Notes Chapter 4 Determinants
Here we have provided CBSE Class 12 Maths Notes Chapter 4 Determinants-Determinants Introduction
Determinants are an essential mathematical concept primarily used in linear algebra. They provide a scalar value associated with square matrices and have wide applications in solving systems of linear equations, finding the area of triangles, and more. The determinant of a matrix helps in determining whether a matrix is invertible, and it plays a crucial role in various fields such as engineering, physics, and economics.Value of a Determinant
Value of determinant of a matrix of order 2, A = [ a 11 a 21 a 12 a 22 ] is Value of determinant of a matrix of order 3, A = ⎡⎣⎢ a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 ⎤⎦⎥ is given by expressing it in terms of second order determinant. This is known as expansion of a determinant along a row (or column). Note (i) For easier calculations of determinant, we shall expand the determinant along that row or column which contains the maximum number of zeroes. (ii) While expanding, instead of multiplying by (-1) i+j , we can multiply by +1 or -1 according to as (i + j) is even or odd. Let A be a matrix of order n and let |A| = x. Then, |kA| = k n |A| = k n x, where n = 1, 2, 3,…Minor: Minor of an element ay of a determinant, is a determinant obtained by deleting the ith row and jth column in which element ay lies. Minor of an element a ij is denoted by M ij .
Note: Minor of an element of a determinant of order n(n ≥ 2) is a determinant of order (n – 1).Cofactor: Cofactor of an element a ij of a determinant, denoted by A ij or C ij is defined as A ij = (-1) i+j M ij , where M ij is a minor of an element a ij .
Note (i) For expanding the determinant, we can use minors and cofactors as (ii) If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero.Singular and non-singular Matrix: If the value of determinant corresponding to a square matrix is zero, then the matrix is said to be a singular matrix, otherwise it is non-singular matrix, i.e. for a square matrix A, if |A| ≠ 0, then it is said to be a non-singular matrix and of |A| = 0, then it is said to be a singular matrix.
Theorems
(i) If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order. (ii) The determinant of the product of matrices is equal to the product of their respective determinants, i.e. |AB| = |A||B|, where A and B are a square matrix of the same order.Adjoint of a Matrix: The adjoint of a square matrix ‘A’ is the transpose of the matrix which obtained by cofactors of each element of a determinant corresponding to that given matrix. It is denoted by adj(A).
In general, adjoint of a matrix A = [a ij ] n×n is a matrix [A ji ] n×n , where A ji is a cofactor of element a ji .Properties of Adjoint of a Matrix
If A is a square matrix of order n × n, then- A(adj A) = (adj A)A = |A| I n
- |adj A| = |A| n-1
- adj (A T ) = (adj A) T
Properties of Determinants
To find the value of the determinant, we try to make the maximum possible zero in a row (or a column) by using properties given below and then expand the determinant corresponding that row (or column). Following are the various properties of determinants: 1. If all elements of any row or column of a determinant are zero, the determinant's value is zero. 2. If each element of any one row or one column of a determinant is a multiple of scalar k, then the value of the determinant is a multiple of k. then the value of the determinant is a multiple of k. i.e. 3. If in a determinant any two rows or columns are interchanged, then the value of the determinant obtained is negative of the value of the given determinant. If we make n such changes of rows (columns) indeterminant ∆ and obtain determinant ∆ , then ∆ 1 = (-1) n ∆. 4. If all corresponding elements of any two rows or columns of a determinant are identical or proportional, then the value of the determinant is zero. [∴ R 1 and R 3 are identical.] 5. The value of a determinant remains unchanged on changing rows into columns and columns into rows. It follows that, if A is a square matrix, then |A’| = |A|. Note: det(A) = det(A’), where A’ = transpose of A. 6. If some or all elements of a row or column of a determinant are expressed as a sum of two or more terms, then the determinant can be expressed as the sum of two or more determinants, i.e. 7. In the elements of any row or column of a determinant, if we add or subtract the multiples of corresponding elements of any other row or column, then the value of determinant remains unchanged, i.e. In other words, the value of determinants remains the same, if we apply the operation R i → R i + kE j or C i → C j → kC j .Inverse of a Matrix and Applications of Determinants and Matrix
1. Inverse of a Square Matrix: If A is a non-singular matrix (i.e. |A| ≠ 0), then
Note: Inverse of a matrix, if exists, is unique.Properties of a Inverse Matrix
- (A -1 ) -1 = A
- (A T ) -1 =(A -1 ) T
- (AB) -1 = B -1 A -1
- (ABC) -1 =C -1 B -1 A -1
- adj (A -1 ) = (adj A) -1
2. Solution of system of linear equations using inverse of a matrix.
Let the given system of equations be a 1 x + b 1 y + c 1 z = d 1 ; a 2 x + b 2 y + c 2 z = d 2 and a 3 x + b 3 y + c 3 z = d 3 . We write the following system of linear equations in matrix form as AX = B, where Case I: If |A| ≠ 0, then the system is consistent and has a unique solution which is given by X = A -1 B. Case II: If |A| = 0 and (adj A) B ≠ 0, then system is inconsistent and has no solution. Case III: If |A| = 0 and (adj A) B = 0, then system may be either consistent or inconsistent according to as the system have either infinitely many solutions or no solutionsArea of a Triangle
Consider a triangle with vertices as ( x 1 , y 1 ) , ( x 2 , y 2 ) (x1,y1),(x2,y2) and ( x 3 , y 3 ) (x3,y3) . We know that the area of the triangle can be found as
A = 1 2 [ x 1 ( y 2 − y 3 ) + x 2 ( y 3 − y 1 ) + x 3 ( y 1 − y 2 ) ] A=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)] .
We can represent the same using determinants as Δ Δ
= 1 2 ∣∣∣∣∣ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ∣∣∣∣∣ 12|x1y11x2y21x3y31| .
We always take the absolute value of the determinant while computing the area as it is a positive quantity.
We use both positive and negative values of the determinant in case the area is given.
We know that three collinear points cannot form a triangle and hence we can say that the area of the triangle formed by three collinear points is zero.
Adjoint of a Matrix
The matrix obtained after taking the transpose of the matrix of cofactors of the given matrix is called the adjoint of that matrix.
For example, if we have the cofactor matrix as
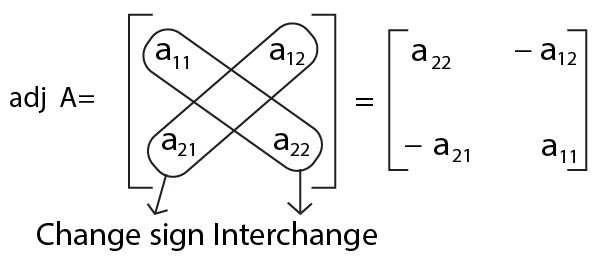
Applications of Determinants and Matrices
-
They can be used for solving systems of linear equations in two or three variables. They can also be used for checking the consistency of a system of linear equations.
-
Consistent system is a system of equations whose solution (one or more) exists.
-
Inconsistent system is a system of equations whose solution does not exist.
-
We can say that the determinant is a number that determines the uniqueness of the solution of a system of linear equations.
Solution of a System of Linear Equations Using Inverse of Matrix
Let us consider system of equations with three variables as
a 1 x + b 1 y + c 1 z = d 1 a1x+b1y+c1z=d1
a 2 x + b 2 y + c 2 z = d 2 a2x+b2y+c2z=d2
a 3 x + b 3 y + c 3 z = d 3 a3x+b3y+c3z=d3
Writing it in matrix form, we have
⎡⎣⎢ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ⎤⎦⎥ ⎡⎣⎢ x y z ⎤⎦⎥ = ⎡⎣⎢ d 1 d 2 d 3 ⎤⎦⎥ [a1b1c1a2b2c2a3b3c3][xyz]=[d1d2d3]
This can be expressed as A X = B AX=B .
Now, we look at two cases:
Case 1: If A A is a non-singular matrix, then its inverse exists.
From A X = B AX=B , we premultiply by A − 1 A−1 ,
A − 1 ( A X ) = A − 1 B A−1(AX)=A−1B
Using associative property,
( A − 1 A ) X = A − 1 B (A−1A)X=A−1B
I X = A − 1 B IX=A−1B
X = A − 1 B X=A−1B
The above matrix equation provides a unique solution for the system of equations as we know that the inverse of a matrix is unique. We call this method as Matrix Method.
Case 2: If A A is a singular matrix, then
is a non-zero matrix, then the solution does not exist and the system of equations is called inconsistent.
If ( a d j A ) B (adj A)B
is a zero matrix, then the system of equations may be either consistent (with infinitely many solutions) or inconsistent (with no solution).
Benefits of CBSE Class 12 Maths Notes Chapter 4 Determinants
- Comprehensive Understanding : The notes provide a clear explanation of the key concepts and properties of determinants, helping students grasp the fundamental principles and their applications in various mathematical problems.
- Time-Saving Revision : These notes provide concise summaries and key points, allowing students to quickly revise the entire chapter before exams.
- Clarification of Properties : The properties of determinants are explained in a simplified manner, aiding students in using them effectively to solve problems efficiently.
- Enhances Problem-Solving Skills : By providing various examples and practice problems, these notes improve students problem-solving abilities and their confidence in tackling determinant-related questions.
CBSE Class 12 Maths Notes Chapter 4 Determinants FAQs
What is a determinant?
What is the significance of a zero determinant?
How do determinants help in solving linear equations?
Can determinants be applied to non-square matrices?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
