CBSE Class 12 Maths Notes Chapter 10 Vector PDF Download
Neha Tanna10 Sept, 2024
Share
CBSE Class 12 Maths Notes Chapter 10: CBSE Class 12 Maths Notes Chapter 10 Vector, focusing on their properties and applications. A vector is a quantity with both magnitude and direction, represented as an arrow in space. It is defined by its initial and terminal points, and its magnitude is the length of the arrow.
Key topics include the types of vectors (zero, unit, position, and co-planar), vector operations like addition, subtraction, and scalar multiplication, and the concept of the dot (scalar) product and cross (vector) product. These operations help solve geometric problems involving lines, planes, and three-dimensional space.CBSE Class 12 Maths Notes Chapter 10 Overview
CBSE Class 12 Maths Notes Chapter 10 Vector, introduces the concept of vectors, which are quantities possessing both magnitude and direction. Vectors are fundamental in physics and engineering as they describe physical quantities like displacement, velocity, and force. The chapter starts with the distinction between scalars (quantities with magnitude only) and vectors, followed by the representation of vectors in two- and three-dimensional space. Key types of vectors discussed include zero vectors, unit vectors, position vectors, and co-planar vectors. The chapter also delves into various operations on vectors, such as vector addition, scalar multiplication, and subtraction, and explains the properties of these operations. Two important vector products are introduced: the dot product (or scalar product) and the cross product (or vector product). The dot product is used to find the angle between two vectors or the projection of one vector on another, while the cross product is useful in determining the area of a parallelogram formed by two vectors and the direction of the resultant vector.CBSE Class 12 Maths Notes Chapter 10 PDF
Here we have provided CBSE Class 12 Maths Notes Chapter 10 Vector for the ease of the students so that they can download it and access it offline.CBSE Class 12 Maths Notes Chapter 10 PDF
CBSE Class 12 Maths Notes Chapter 10 Vector
Here we have provided CBSE Class 12 Maths Notes Chapter 10 Vector - Physical quantities that have linked directions and magnitudes are described by the concept of vectors. A scalar is a physical quantity that has only one value or constant that may fully represent it. Vector algebra in class twelve Chapter 10 of NCERT Maths covers a number of key ideas related to this subject, including vector types and operations. The main topics of this lesson are the introduction to vectors, their different types, and operations on them, such as addition, which are covered in the class 12 Maths vector algebra chapter. A vector is a quantity in physics that possesses both magnitude and direction. Stated differently, an object that possesses both magnitude and direction is referred to as a vector. It explains how the object moves from one place to another. The vector with head, tail, magnitude, and direction is depicted in the image below.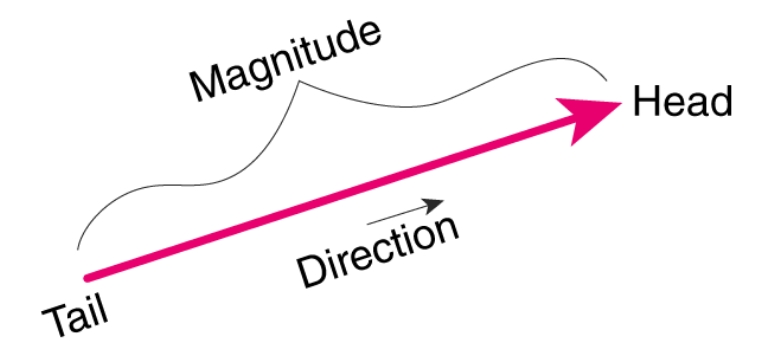
Types of Vectors List
There are 10 types of vectors in mathematics which are:- Zero Vector
- Unit Vector
- Position Vector
- Co-initial Vector
- Like and Unlike Vectors
- Co-planar Vector
- Collinear Vector
- Equal Vector
- Displacement Vector
- Negative of a Vector
Laws of Vector Addition
A physical quantity that may be expressed in both direction and magnitude is called a vector. We are going to learn how to add various vectors in the next discussion. The following are the many vector addition laws:Triangle law of vector addition - The Triangle Law of Vector Addition is a method to add two vectors geometrically. According to this law, if two vectors are represented by two sides of a triangle taken in the same order, their resultant vector is given by the third side of the triangle taken in the reverse order.
Parallelogram law of vector addition - The Parallelogram Law of Vector Addition is a geometric method for adding two vectors. According to this law, if two vectors are represented by two adjacent sides of a parallelogram, the diagonal passing through the common point of the vectors represents their resultant.
Multiplication of Vectors
Multiplication of vectors can be of two types:(i) Scalar Multiplication
(ii) Vector Multiplication
Here, we will discuss only the Scalar Multiplication byMultiplication of vectors with scalar
A vector's direction stays constant when it is multiplied by a scalar quantity, but the vector's magnitude varies according to the scalar's magnitude.
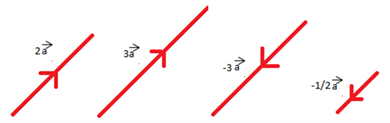From the above-given set of vectors we see that the direction of vector
remains the same when the scalar value is positive and changes to the exact opposite direction when the scalar value is negative. The magnitude varies in both situations based on the values of the scalar multiple.
According to the discussions above, it is evident that
Also, as per the above discussion, if
k =
0 then the vector also becomes zero.
Let us go through an example to make this point more clear,
Components of a Vector Definition
Let's say a vector V has a definition on a plane with two dimensions. Two parts, such as vx and vy, make up the vector V. Let us now create an angle θ between the vector V and its x-component. Drawn parallel to the y-component (vy), the vector V and its x-component (vx) form a right-angled triangle. By trigonometric ratios, we know, cos θ = Adjacent Side/Hypotenuse = v x /V sin θ = Opposite Side/Hypotenuse = v y /V where V is the magnitude of the vector V.Components of vector formula
Since, in the previous section we have derived the expression: cos θ = v x /V sin θ = v y /V Therefore, the formula to find the components of any given vector becomes:v x =V cos θ
v y =Vsin θ
Where V is the magnitude of vector V and can be found using Pythagoras theorem;|V| = √(v x 2 , v y 2 )
Vector Product
A thing with both direction and magnitude is called a vector. While the arrow denotes the direction of the vectors, the length represents their magnitude. Vectors come in several forms. There are two methods to multiply vectors in general.(i) Dot product of vectors (also known as Scalar product)
(ii) Cross product of vectors (also known as Vector product).
Cross product of Vectors (Vector Product)
The vector product of two vectors a and b is given by a vector whose magnitude is given by
will be in the same direction as the rotation of a right-handed screw if moved similarly. Furthermore, the provided vectors, a and b, are non-parallel and non-null vectors. The direction of the resulting vector can be estimated using the right-hand thumb rule.
Benefits of CBSE Class 12 Maths Notes Chapter 10
The benefits of studying Chapter 10 Vectors from CBSE Class 12 Maths notes are numerous and crucial for mastering both theoretical concepts and practical applications:Conceptual Clarity : The notes help in understanding the fundamental concepts of vectors, including magnitude, direction, and different types of vectors like zero vectors, unit vectors, and co-planar vectors.
Simplified Learning : Well-organized notes condense the complex topic into digestible sections, making it easier to grasp operations like vector addition, subtraction, scalar multiplication, dot product, and cross product.
Enhanced Problem-Solving Skills : Vector algebra is essential for solving problems related to geometry and physics. Mastery of these notes helps in applying vector concepts to solve questions involving 3D space, lines, and planes.
Exam Preparation : Summarized notes provide a quick revision tool, allowing students to recall formulas and important concepts efficiently, aiding in effective preparation for board exams and competitive tests.
Foundation for Advanced Studies : Understanding vectors is critical for higher studies in fields like engineering, physics, and computer science, as they are widely used in mechanics, electromagnetism, and 3D modeling.
CBSE Class 12 Maths Notes Chapter 10 FAQs
What is the objective of vector algebra?
What are the principles of vector algebra?
Why vectors are not divided?
What is the full concept of a vector?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
