CBSE Class 12 Maths Notes Chapter 13:
CBSE Class 12 Maths Notes Chapter 13 Probability, building upon the foundational concepts from earlier classes. This chapter covers advanced topics such as conditional probability, Bayes' theorem, random variables, probability distributions, and binomial distribution. Students learn to calculate probabilities in complex scenarios, including dependent and independent events.
The chapter also explores the concept of the expectation of a random variable, providing insight into expected outcomes. These topics have broad applications in fields like statistics, economics, and data science, making probability a crucial tool for decision-making and predictive analysis in real-world situations.
CBSE Class 12 Maths Notes Chapter 13 Overview
CBSE Class 12 Maths Notes Chapter 13 Probability, delves into advanced concepts, building on previous knowledge of basic probability. It covers topics like conditional probability, where the probability of an event is determined based on the occurrence of another event, and independent and dependent events, distinguishing between cases where events influence each other. A major highlight is Bayes' Theorem, which revises probability estimates with new information.
The chapter also introduces random variables and their probability distributions, exploring how random events can be modeled mathematically. The binomial distribution, a key concept, is used to analyze situations with a fixed number of independent trials, focusing on the number of successes.
These concepts find applications in real-life scenarios, such as decision-making under uncertainty, predictions in data analysis, and risk management. By understanding probability theory at an advanced level, students develop a strong foundation for higher studies in fields like statistics, economics, and engineering, while also preparing for competitive exams.
CBSE Class 12 Maths Notes Chapter 13 PDF
Below we have provided CBSE Class 12 Maths Notes Chapter 13 pdf for the ease of students so that they can easily download it and access it without internet.
CBSE Class 12 Maths Notes Chapter 13 PDF
CBSE Class 12 Maths Notes Chapter 13 Probability
Below we have CBSE Class 12 Maths Notes Chapter 13 Probability -
Event:
An event, also known as a case, is a subset of the sample space related to a random experiment.
For instance, when a coin is tossed, receiving head or tail is an event.
Equally Likely Events:
If none of the occurrences are predicted to happen more frequently than the other, they are considered equally likely.
For example, if a die is thrown impartially, there is an equal chance of all six faces appearing.
Mutually Exclusive Events:
When two occurrences happen one after the other, they are said to be mutually exclusive. For example, if A and B are mutually exclusive, then (A ∩ B) = Φ. When rolling a die, each of the six faces, numbered 1 through 6, is mutually exclusive since it eliminates the chance of any other faces appearing in the same trial.
Exhaustive Events:
If at least one of the events in the set occurs every time the experiment is conducted, then the set is considered exhaustive.
If E
1
, E
2
, …, E
n
are exhaustive events, then E
1
∪ E
2
∪……∪ E
n
= S.. The total number of cases in a two-dice toss is 6 squares = 36. Given that any of the six numbers on the second die can be connected to any of the numbers 1 through 6 on the first die.
Complement of an Event:
Let A be an event in a sample space S, then the complement of A is the set of all sample points of the space other than the sample point in A and it is denoted by A’or
A
¯
.
i.e. A’ = {n : n ∈ S, n ∉ A]
Note:
(i) An experiment is a procedure that yields certain, predetermined results.
(ii) A random experiment is one in which, although being conducted under the exact same conditions, the results might differ.
Probability of an Event
The
probability of an event
is a measure of the likelihood that a particular event will occur. It is expressed as a number between 0 and 1, where:
-
0
means the event is impossible (it will not occur).
-
1
means the event is certain (it will definitely occur).
Conditional Probability:
Conditional probability
is the probability of an event occurring, given that another event has already occurred. It helps in understanding how the likelihood of one event changes when another related event is known to have happened.
Mathematically, the conditional probability of event A occurring given that event B has already occurred is denoted by P(A | B) and is calculated using the formula: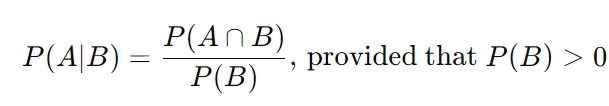
Where:
-
P(A ∩ B) is the probability that both events A and B occur.
-
P(B) is the probability of event B occurring.
Properties of Conditional Probability:
If E and E are two events of sample space S and G is an event of S which has already occurred such that P(G) ≠ 0, then
(i) P[(E ∪ F)/G] = P(F/G) + P(F/G) – P[(F ∩ F)/G], P(G) ≠ 0
(ii) P[(E ∪ F)/G] = P(F/G) + P(F/G), if E and F are disjoint events.
(iii) P(F’/G) = 1 – P(F/G)
(iv) P(S/E) = P(E/E) = 1
Multiplication Theorem:
If E and F are two events associated with a sample space S, then the probability of simultaneous occurrence of the events E and F is
P(E ∩ F) = P(E) . P(F/E), where P(F) ≠ 0
or
P(E ∩ F) = P(F) . P(F/F), where P(F) ≠ 0
This result is known as multiplication rule of probability.
Baye’s Theorem and Probability Distributions
Partition of Sample Space: A set of events E
1
, E
2
,…,E
n
is said to represent a partition of the sample space S, if it satisfies the following conditions:
(i) E
i
∩ E
j
= Φ; i ≠ j; i, j = 1, 2, …….. n
(ii) E
1
∪ E
2
∪ …… ∪ E
n
= S
(iii) P(E
i
) > 0, ∀ i = 1, 2,…, n
Random Variable:
The domain of a random experiment is the sample space, and a random variable is a real-valued function with this property. It is typically represented by the capital letter X.
It is possible to define many random variables in the same sample space.
Bernoulli Trial:
Trials of a random experiment are called Bernoulli trials if they satisfy the following conditions:
(i) There should be a finite number of trials.
(ii) The trials should be independent.
(iii) Each trial has exactly two outcomes, success or failure.
(iv) The probability of success remains the same in each trial.
Benefits of CBSE Class 12 Maths Notes Chapter 13
The benefits of studying Chapter 13 Probability in CBSE Class 12 Mathematics include:
Real-Life Application
: Probability concepts are widely used in various fields like statistics, economics, data science, and engineering, helping students understand uncertainty and make informed decisions.
Problem-Solving Skills
: Students learn to approach complex scenarios using logical thinking, which enhances their problem-solving abilities, especially in uncertain situations.
Foundation for Higher Studies
: Advanced topics like Bayes’ Theorem, random variables, and probability distributions provide a strong base for further studies in mathematics, statistics, and other analytical disciplines.
Decision-Making
: Understanding probability helps students in decision-making under uncertainty, which is essential for fields like finance, insurance, and business.
Competitive Exams
: Probability is a critical topic in competitive exams like JEE, NEET, and various entrance tests, making it an important area for scoring well.
Analytical Thinking
: It promotes critical thinking by encouraging students to analyze situations and predict outcomes based on mathematical models.
