CBSE Class 12 Maths Notes Chapter 8 Application of Integrals
Here we have provided CBSE Class 12 Maths Notes Chapter 8 Application of Integrals for the ease of the students so that they can prepare better for their exams.
Neha Tanna9 Sept, 2024
Share
CBSE Class 12 Maths Notes Chapter 8: CBSE Class 12 Maths Notes Chapter 8 Application of Integrals focuses on using definite integrals to find areas under curves and between curves. It covers how to calculate the area of regions bounded by a curve, a line, or between two curves in both Cartesian and polar coordinates.
The chapter explains the process of determining the limits of integration and integrating functions to find the desired area. These techniques are essential in solving real-world problems involving geometry, physics, and engineering. It provides a deeper understanding of how integrals can be applied in practical scenarios.CBSE Class 12 Maths Notes Chapter 8 Overview
CBSE Class 12 Maths Notes Chapter 8 Application of Integrals primarily deals with finding the area of regions under curves using definite integrals. The chapter focuses on the practical application of integration, particularly in calculating areas between curves and along specific boundaries in both Cartesian and polar coordinates. It begins by explaining how to calculate the area under a curve and between two curves by setting up definite integrals with appropriate limits. These integrals help in finding the exact area confined by given curves, which is essential in solving real-world problems. The chapter emphasizes understanding the geometric interpretation of integrals, allowing students to calculate areas enclosed by curves with precision. This concept has significant applications in fields like physics, engineering, economics, and biology. It helps in solving problems related to motion, areas of irregular shapes, and other mathematical models where precise measurements are required. Mastery of this chapter enables students to appreciate how integrals are used in real-life applications beyond mere calculations.CBSE Class 12 Maths Notes Chapter 8 PDF Download
Here we have provided CBSE Class 12 Maths Notes Chapter 8 Application of Integrals pdf for the ease of the students. Students can download this pdf and access it without internet.CBSE Class 12 Maths Notes Chapter 8 PDF
CBSE Class 12 Maths Notes Chapter 8 Application of Integrals
Here we have provided CBSE Class 12 Maths Notes Chapter 8 Application of Integrals -Integration
Properties of Definite Integrals
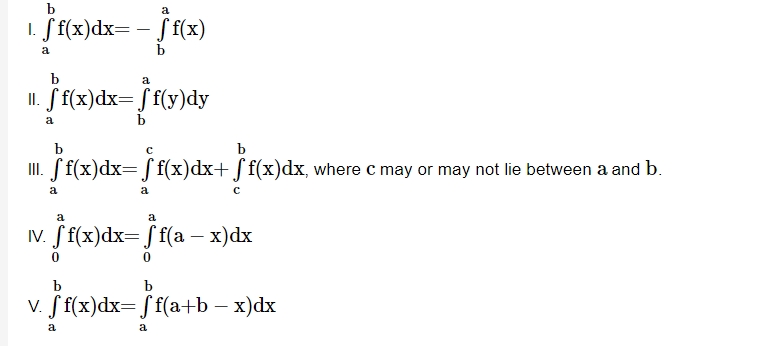
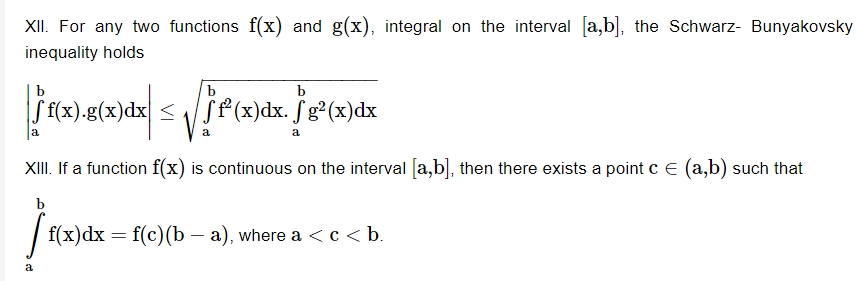
Differentiation Under Integral Sign
Newton Leibnitz’s Theorem
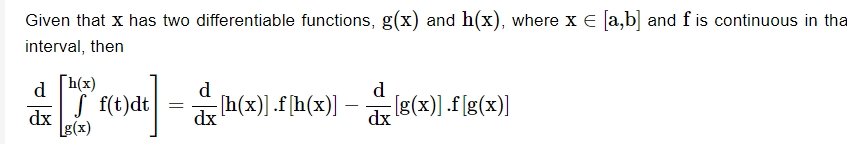
Definite Integral as a Limit of Sum
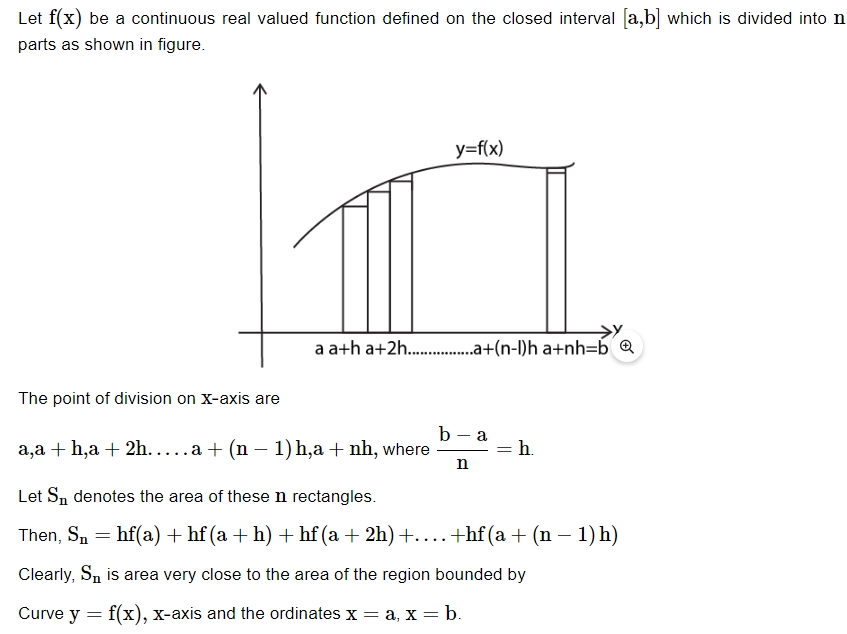
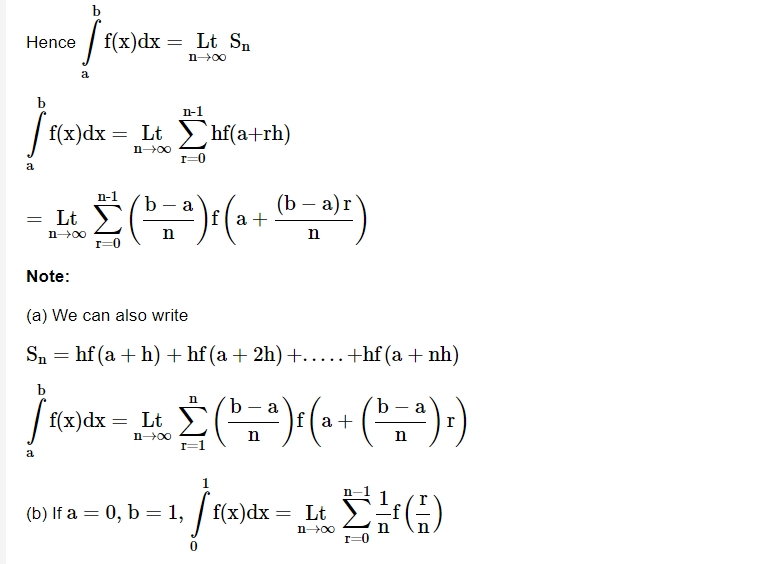
Steps to Express the Limit of Sum as Definite Integral
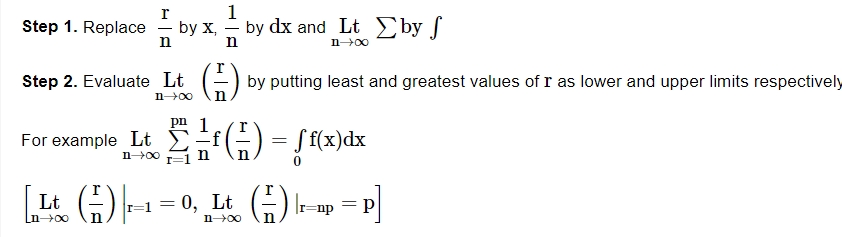
Reduction Formulae in Definite Integrals
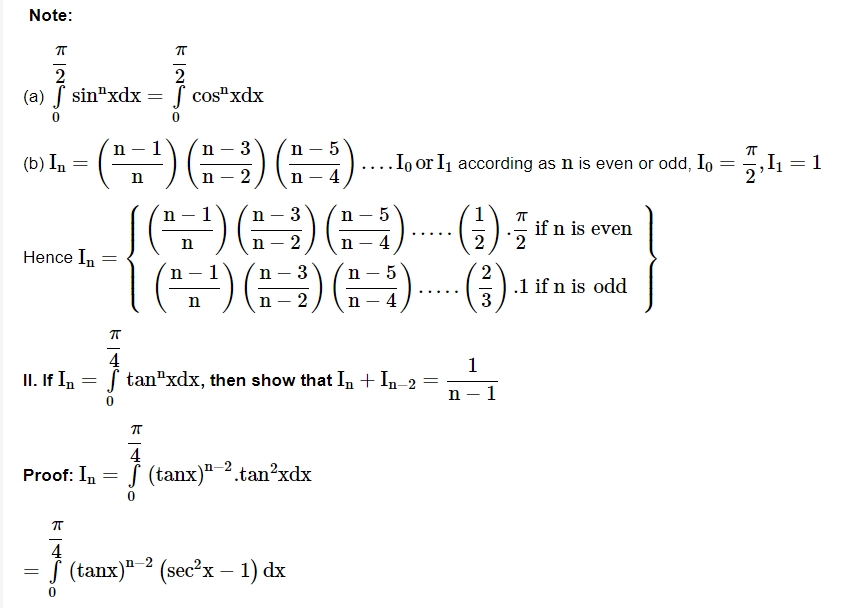
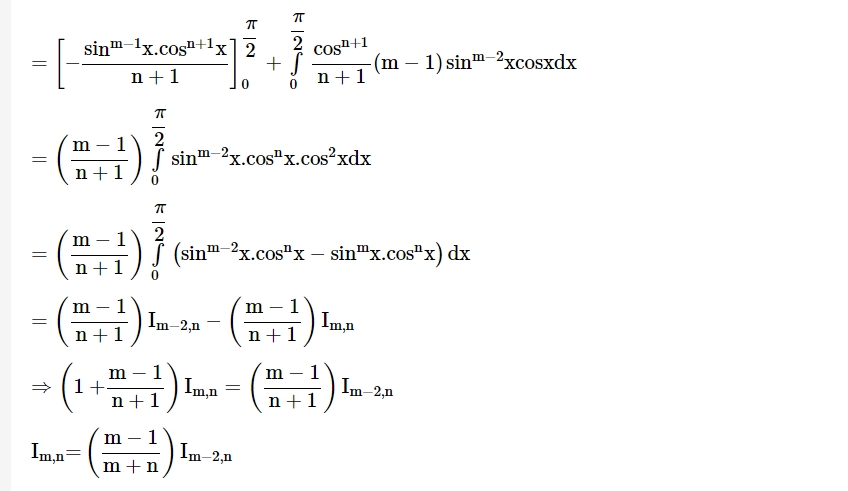
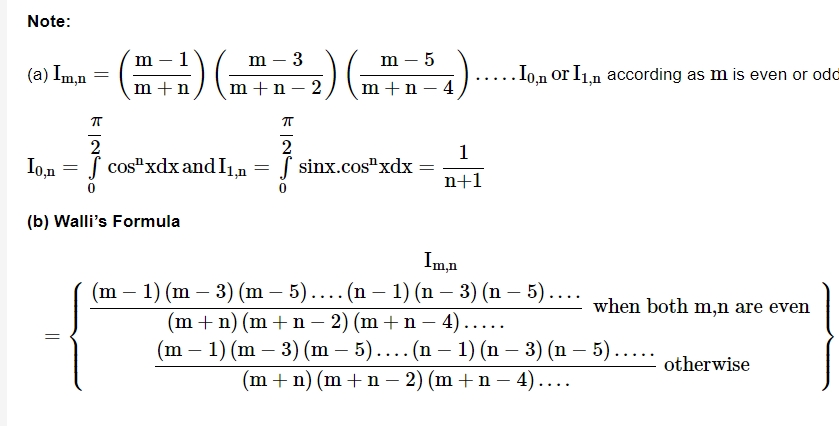
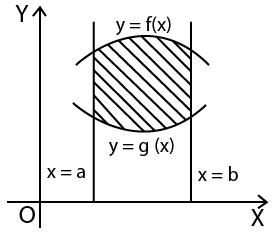
Area Under the Curves
(a) Area of Plane Regions:
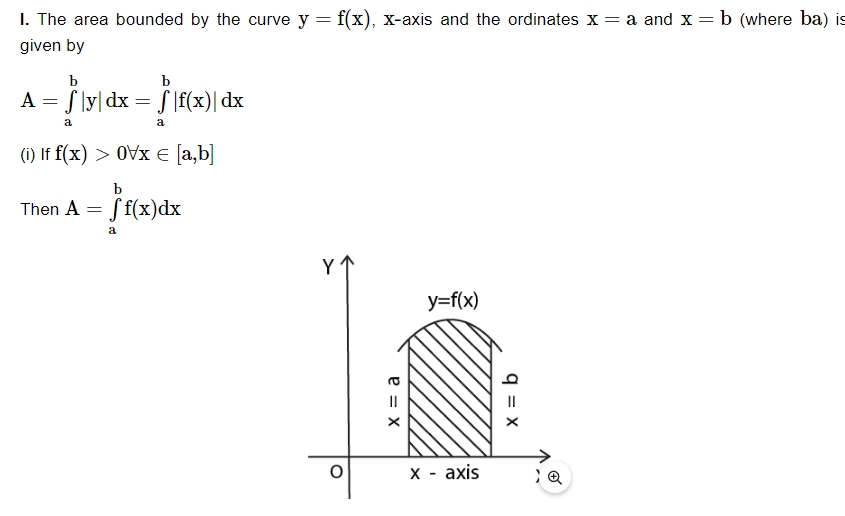
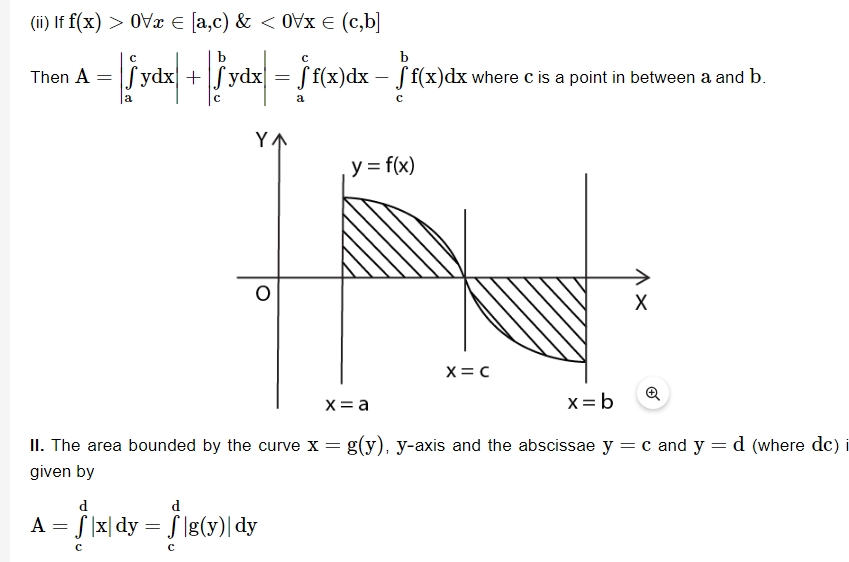
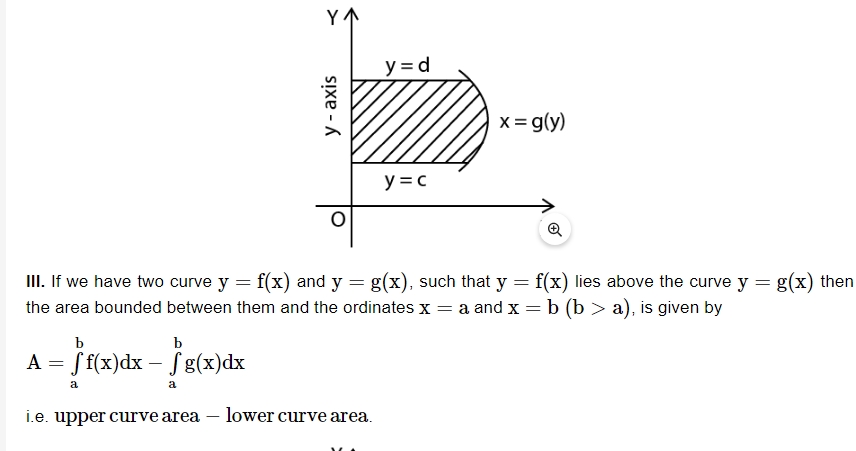
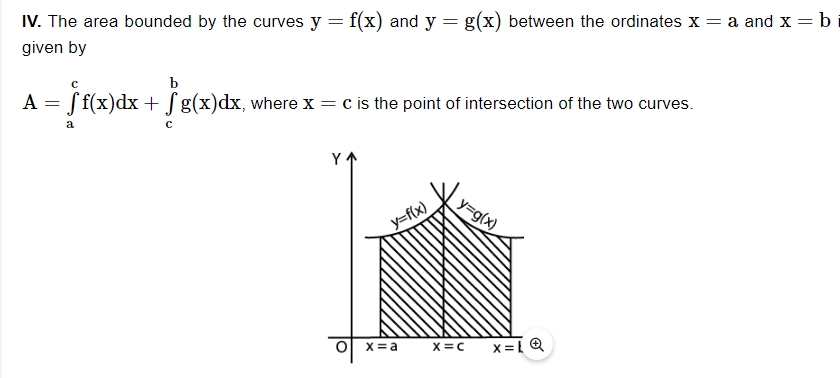
V. Curve Tracing
To find the area surrounded by many curves, a preliminary sketch of the target component is required. For the purpose of tracing a cartesian curve f(x,y)=0, the following procedures are quite helpful.
Step 1: Symmetry
(i) The curve is symmetrical about the x-axis if all of the powers of y in the supplied curve's equation are even. (ii) The curve is symmetrical about the y-axis if every power of x in the provided curve's equation is even. (iii) The curve is symmetrical about the line y=x if the supplied curve's equation does not change when x and y are switched. (iv) The given curve is symmetrical in opposing quadrants if the equation stays the same when x and y are substituted with −x and −y, respectively.Step 2: Origin
The algebraic curve goes through the origin if there isn't a constant term in its equation. The lowest degree terms in the equation of the given algebraic curve are then equated to zero to get the tangents at the origin.Step 3: Intersection with the Co-ordinates Axes
(i) To estimate the sites of intersection of the curve with the x-axis, find the relevant values of x by solving the provided curve's equation with y=0. (ii) To estimate the sites of intersection of the curve with the y-axis, find the corresponding values of y by substituting x=0 in the equation of the provided curve.Step 4: Asymptotes
Discover where the curve's asymptotes are. (i) The provided algebraic curve's vertical asymptotes, or asymptotes parallel to the y-axis, are obtained by setting the coefficient of the largest power of y in the supplied curve's equation to zero. (ii) By setting the coefficient of the largest power of x in the equation of the supplied curve to zero, the horizontal asymptotes of the given algebraic curve, or asymptotes parallel to the x-axis, are obtained.Step 5: Region
Determine which areas of the plane contain no portion of the curve. We solve the provided equation for y in terms of x, or vice versa, to find such regions. Assuming y turns imaginary for x>a, the curve does not fall inside the x>a area.Step 6: Critical Points
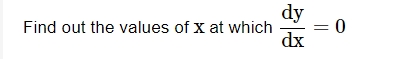Around these moments, y typically shifts from being a rising function of x to a decreasing function of x, or the opposite.
Step 7:
Trace the curve with the help of the above points.
Benefits of CBSE Class 12 Maths Notes Chapter 8
The benefits of studying CBSE Class 12 Maths Chapter 8 Application of Integrals are numerous, as it provides students with practical mathematical tools for solving real-life problems. Some key benefits include:Understanding Area Calculation : Students learn to calculate the area under curves and between curves, which is useful in geometry, physics, and engineering.
Real-World Applications : The concepts taught in this chapter have practical applications in various fields such as economics, biology, and architecture, where understanding the area between curves is important.
Enhanced Problem-Solving Skills : The chapter improves critical thinking by encouraging students to analyze functions and boundaries to set up integrals, fostering logical reasoning and mathematical precision.
Foundation for Advanced Studies : A strong grasp of this chapter is essential for higher studies in mathematics, engineering, data science, and other fields that involve integral calculus.
Exam Relevance : The application of integrals is a frequent topic in board exams, and mastering this chapter can help students score better by tackling both theoretical and application-based questions effectively.
Integration with Other Topics : Understanding this chapter helps connect various other mathematical concepts such as differential equations, kinematics, and volume calculations.
CBSE Class 12 Maths Notes Chapter 8 FAQs
What is the real world application of integrals?
Integrals are utilised in a variety of sectors in real life, including engineering, where engineers use integrals to determine the geometry of a building. It's used to describe the centre of gravity, among other things, in physics. In the field of graphical representation, three-dimensional models are displayed.
What is the use of application of integrals?
In maths, the application of integral is made to determine the area under a curve, the area between two curves, the center of mass of a body, and so on.
What is the purpose of using integral?
An integral is a function, of which a given function is the derivative. Integration is basically used to find the areas of the two-dimensional region and computing volumes of three-dimensional objects. Therefore, finding the integral of a function with respect to x means finding the area to the X-axis from the curve.
What do integrals help us find?
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.