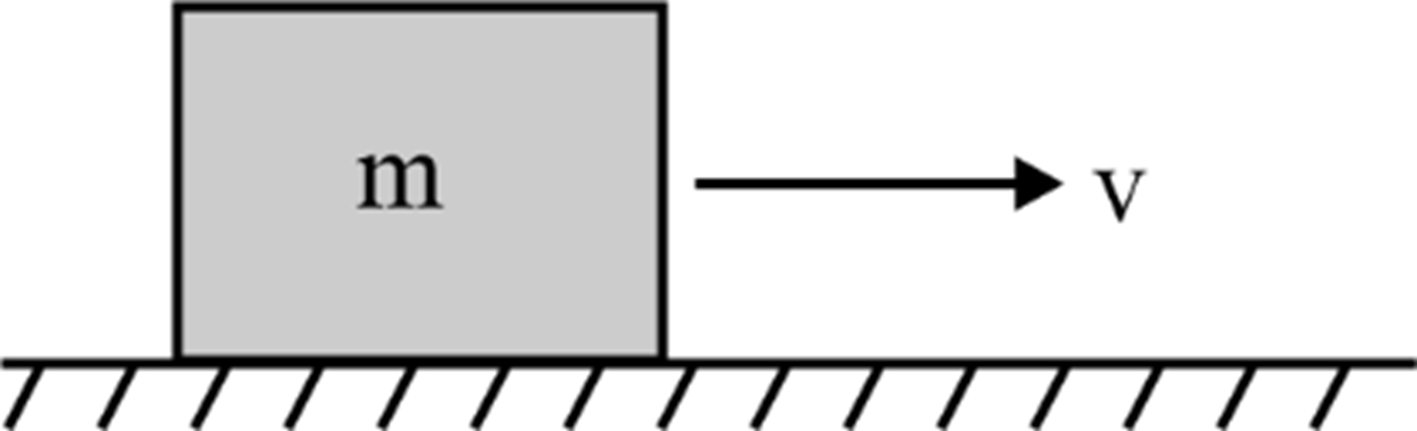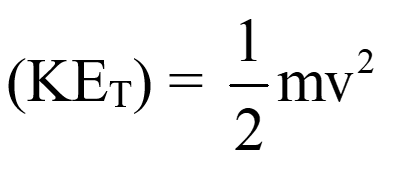Work Energy Principle:
In engineering, some problems involve understanding what makes objects move and how they move. This falls under the branch of dynamics known as "kinetics." Kinetics is a branch of mechanics that deals with the study of forces and their effects on the motion of particles and rigid bodies. In engineering mechanics, understanding the kinetics of particles and rigid bodies is fundamental to solving practical engineering problems.
The Work-Energy Principle is a fundamental tool that helps us analyze the behavior of particles and rigid bodies by considering the work done on them and the changes in their mechanical energy.
Work
The work done on an object by a force is defined as the product of the force or couple applied on the particle or rigid body and the displacement (i.e., linear displacement or rotation) of the object in the direction of the applied effort. Work is a scalar quantity, and its SI unit is the joule. Mathematically, work done (W) is expressed as:
Where, F(s) is the force as a function of position, and s
2
and s
1
are the initial and final positions, respectively. From the above equation, it can also be concluded that the area under the force-displacement (F−s) curve between two positions s
1
and s
2
represents the work done by the force acting on an object.
Note:
If the net force is the constant (i.e., not the function of position), then
W = Net force × Displacement = ΣF × s
Work done by various forces and moments acting on the body is given as follows:
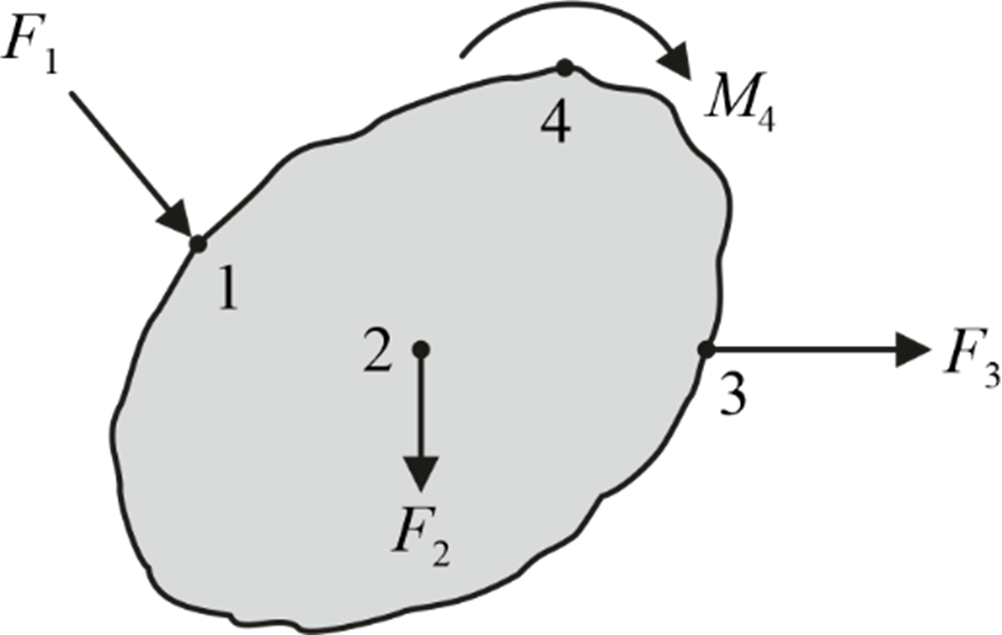
W
net
= Σ(F × s) + Σ(M × θ) = ± F
1
s
1
± F
2
s
2
± F
3
s
3
± M
4
θ
4
Note:
When the force and displacement are perpendicular to each other, no work is done.
Energy
Energy can be described as the ability to perform tasks, and it can take on various forms, including mechanical, electrical, chemical, heat, light, sound, and more. In the field of Engineering Mechanics, our primary focus is on mechanical energy. Mechanical energy can be categorized into two main types: (i) potential energy and (ii) kinetic energy. A physical object can possess either one or both of these types of mechanical energy.
-
Potential Energy:
Potential energy, also called datum energy, refers to the energy of an object based on its position relative to a reference point. In Engineering Mechanics, it's crucial to consider the potential energy resulting from gravity (weight) and an elastic spring.
-
Kinetic Energy:
Kinetic energy is the energy an object has due to its motion. There are two types of kinetic energy that a body can possess.
|
Kinetic Energy due to Translational Motion
|
Kinetic Energy due to Rotational Motion
|
|
-
Translational Kinetic Energy (KE
T
) of the block is given as;
Where m is the mass of the object and v is the velocity of the object at a given instant.
|
-
Rotational Kinetic Energy of the object is given as;
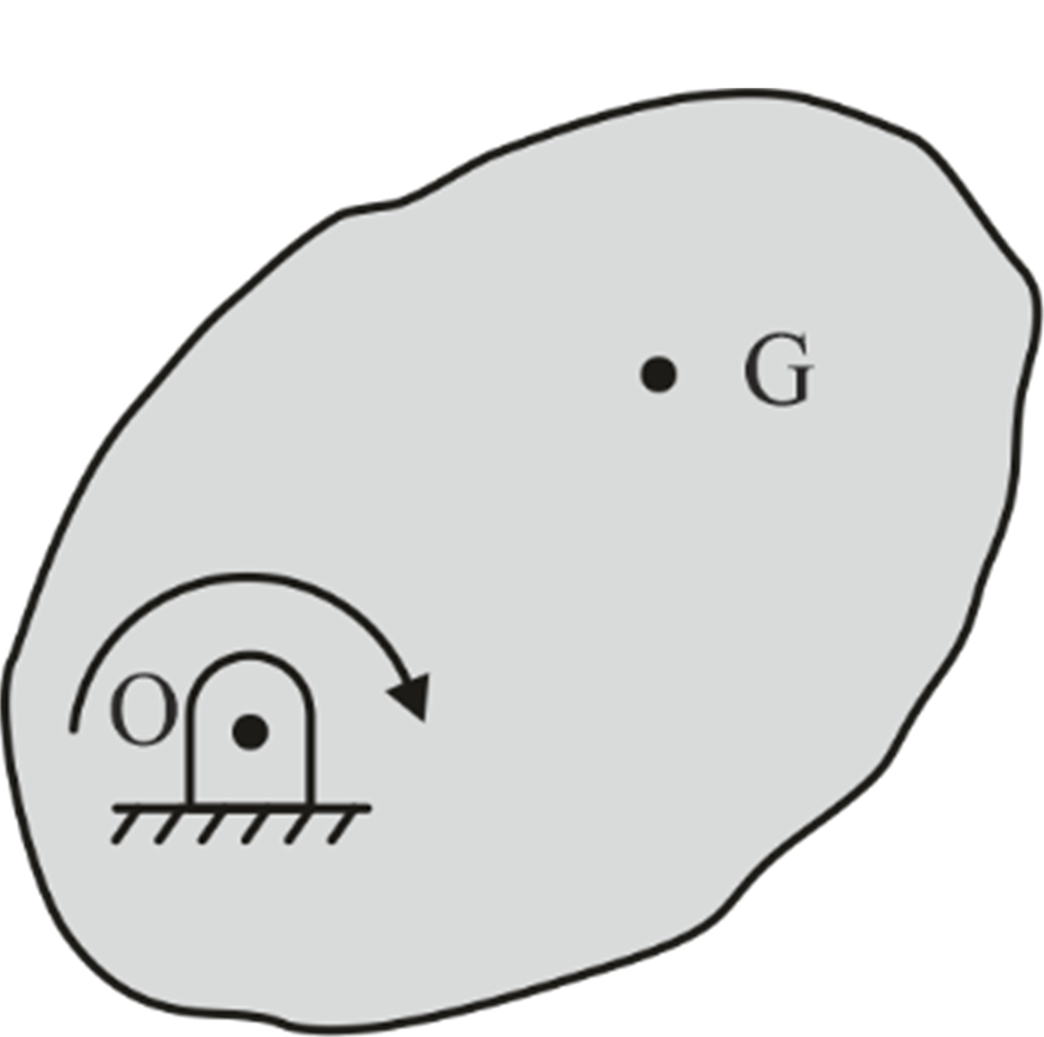
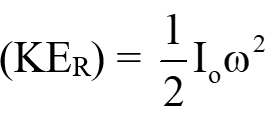
Where I
O
is the mass moment inertia of the object about point of rotation and ω is the angular velocity of the object at a given instant.
|
Note:
If the object has a combination of translational motion and rotational motion, then its kinetic energy is given as follows:
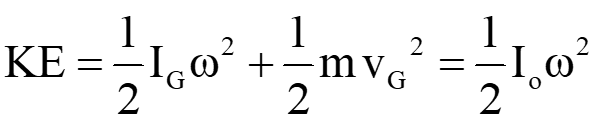
Where m is the mass of the object, I
G
and I
o
are the mass moment inertia of the object about its center of mass and instantaneous center respectively, ω is the angular velocity of the object, and v
G
is the velocity of the center of mass at a given instant.
Work Energy Principle
It states that the net work performed by the combined forces and moments acting upon a body is equal to the difference between its final and initial kinetic energy.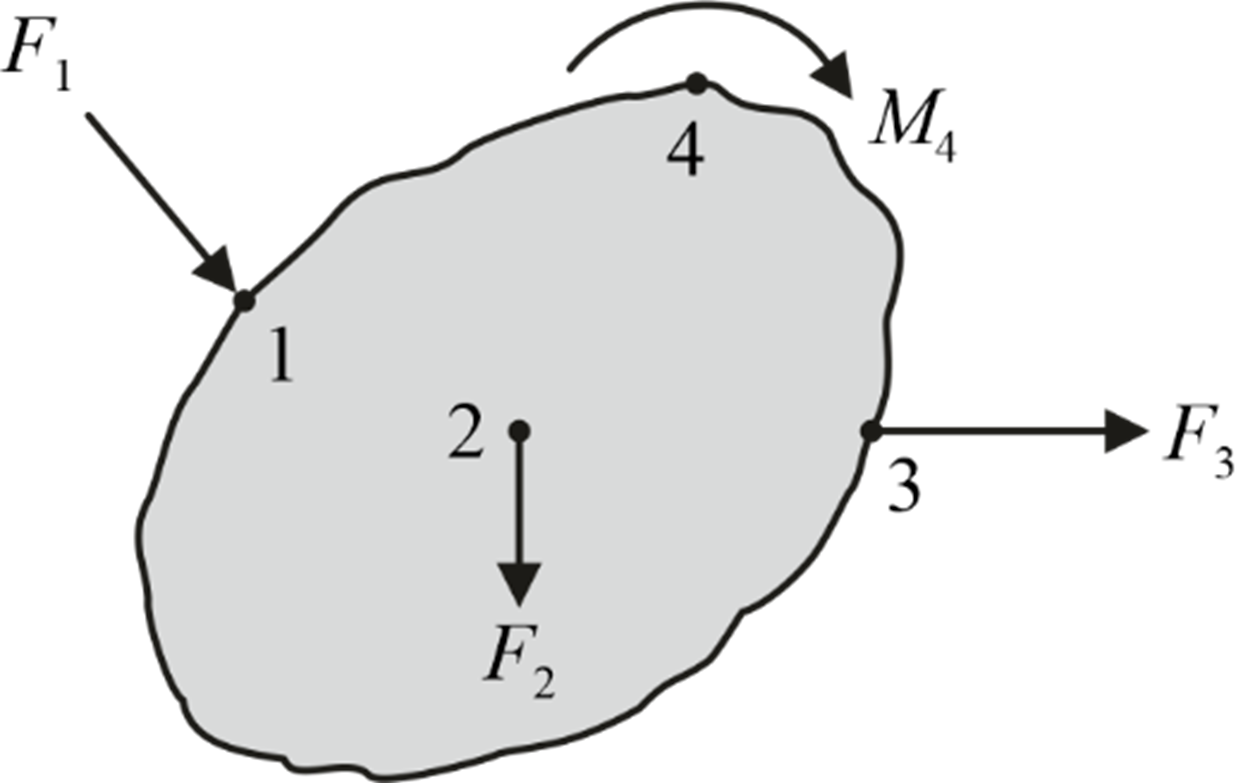
Work done on body = Final kinetic energy – Initial kinetic energy
W
net
= (K.E.)
f
– (K.E.)
i
Note
-
If the object is a particle (meaning rigid body does not undergo rotational motion), then the Work-Energy Principle for a particle can be expressed mathematically as follows:
-
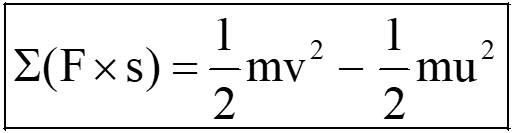
if the net force and the couple on the rigid body is the function of displacement, then
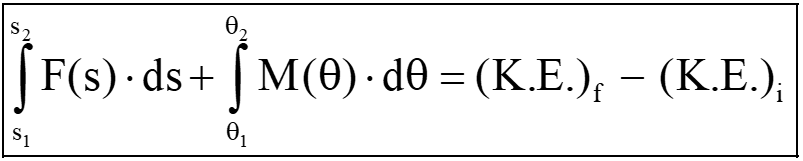
Conservation of Mechanical Energy
If the work done by the non-conservative force on the body is zero, then the sum of kinetic and potential energies of the particle or rigid body remains constant.
(Kinetic Energy + Potential Energy)
1
= (Kinetic Energy + Potential Energy)
2
Note
: Conservative forces refer to a specific type of force field or interaction in which the work done by the force on an object depends only on the initial and final positions of that object and is independent of the path taken between these positions. In contrast, non-conservative forces have work that varies depending on the specific path between those positions.
