Angle Formulas: Definition, Different Types, Solved Examples

Angle formulas are employed to determine the measurements of angles. An angle materializes when two intersecting rays, referred to as the arms of the angle, meet at a common endpoint. The point where these arms intersect is recognized as the vertex of the angle. An angle quantifies the degree of rotation between these two lines. Radians and degrees are both units of measurement for angles. In this discussion, we will explore the formulas for central angles in a circle, as well as formulas for multiple angles and double angles, accompanied by a selection of solved examples.

What Are Angle Formulas?

In this context, we've covered angle formulas related to the central angle formed by two radii and the corresponding arc in a circle. Now, let's delve into trigonometric formulas for multiple angles and double angles.

Also Check - Rational Formula

Multiple Angle Formulas

Multiple angles typically arise within trigonometric functions. Calculating the precise values of these multiple angles directly can be challenging, but it's achievable by expanding each trigonometric function into its extended form. Expressions for multiple angles like sin(nx), cos(nx), and tan(nx) are established exclusively in terms of sin(x) and cos(x), thanks to Euler's formula and the Binomial Theorem. Mathematics employs a set of multiple angle formula identities for these purposes.

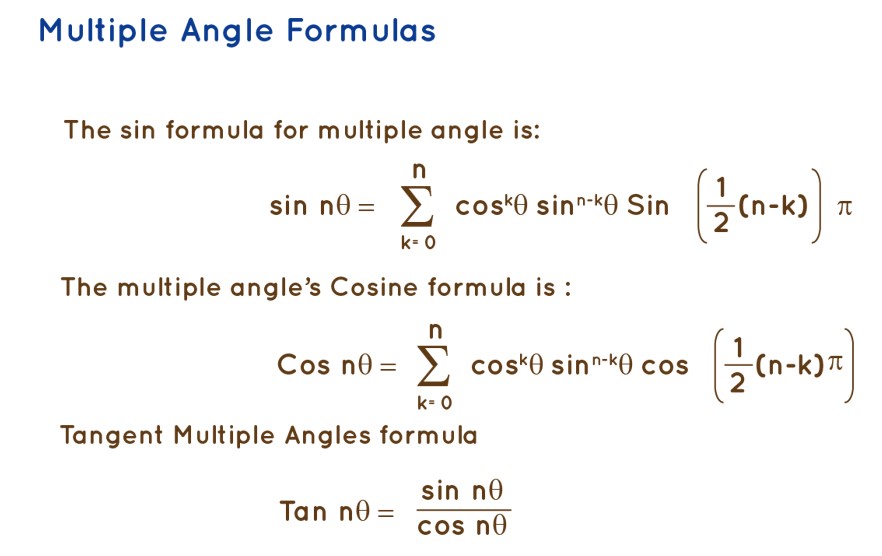
Formula 1: The trigonometric expression for multiple angles in terms of sine is as follows:

where n=1,2,3,……

General formulas are,

Sin2θ =2 × Cosθ.Sinθ

Sin3θ =3Sinθ - 4Sin 3 θ

Formula 2: The formula for expressing multiple angles in terms of cosine is presented below:

where n = 1,2,3

The general formula goes as:

Cos2θ = Cos 2 θ – Sin 2 θ

Cos3θ = 4Cos 3 θ – 3Cosθ

Formula 3: The formula for expressing multiple angles in terms of tangent is as follows:

Tan nθ= Sin nθ/ Cos nθ

Where n = 1,2,3....

Double Angle Formulas

Double angle formulas serve to express trigonometric ratios of double angles (2θ) in terms of those for single angles (θ). These formulas are derived from the sum formulas of trigonometry and can also be derived using Pythagorean identities. To obtain the double angle formulas for sine, cosine, and tangent, we substitute A = B into the sum formulas. Additionally, we derive alternative formulas using Pythagorean identities.

The double angle formulas for sine, cosine, and tangent are as follows:

• sin 2A = 2 sin A cos A (or) (2 tan A) / (1 + tan 2 A)
• cos 2A = cos 2 A - sin 2 A (or) 2cos 2 A - 1 (or) 1 - 2sin 2 A (or) (1 - tan 2 A) / (1 + tan 2 A)
• tan 2A = (2 tan A) / (1 - tan 2 A)

What is Central Angle of Circle Formula?

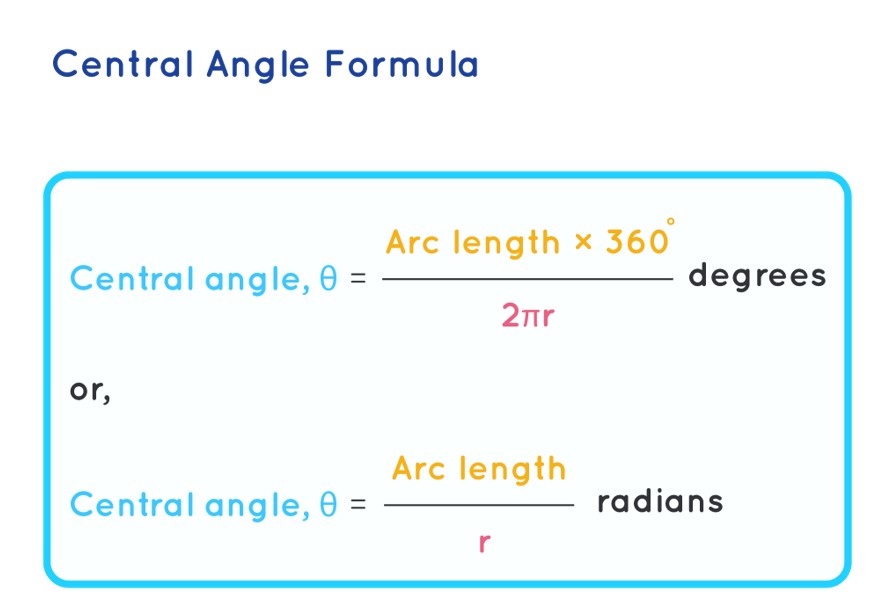
The central angle formula for a circle allows us to determine the angle formed between two radii or the angle subtended by the circle's arc and the two radii emanating from the circle's center. The central angle is defined by the radius vectors serving as its arms. To compute the central angle, you need two pieces of information: the measurement of the arc length that the central angle subtends at the circle's center and the radius of the circle. The formula for the central angle of a circle is expressed as follows:

Central angle, θ = (Arc length × 360º) / (2πr) degrees or

Central angle, θ = Arc length / r radians, where r represents the radius of the circle.

Also Check - Absolute Value Formula

Angle Formulas Examples

Example 1: Jill possesses a circular segment with an arc length of 7π units and a radius of 9 units. Let's determine the segment's angle using the angle formula.

Solution:

Arc length = 7π (given)

Radius = 9 units (given)

Utilizing the angle formula:

Angle = (Arc Length × 360°) / (2πr)

Angle = (7π × 360°) / (2π × 9)

= 140°

Hence, the angle of the segment is 140 degrees.

Example 2: Given that tan A = 3/4, let's determine the values of sin 2A, cos 2A, and tan 2A.

Solution:

We can use the double angle formulas to find sin 2A, cos 2A, and tan 2A. First, we need to find sin A and cos A using the given information:

tan A = 3/4

We can find sin A and cos A using the Pythagorean identity:

sin^2 A + cos^2 A = 1

(3/4)^2 + cos^2 A = 1

9/16 + cos^2 A = 1

cos^2 A = 1 - 9/16

cos^2 A = 7/16

cos A = ±√(7/16)

Since A is an acute angle, cos A is positive:

cos A = √(7/16)

cos A = √7/4

cos A = √7/4 * 2/2

cos A = √7/8

Now that we have sin A and cos A, we can calculate sin 2A, cos 2A, and tan 2A using the double angle formulas:

sin 2A = 2 sin A cos A

sin 2A = 2 * (3/5) * (√7/8)

sin 2A = (3√7) / 20

cos 2A = cos^2 A - sin^2 A

cos 2A = (√7/8)^2 - (3/5)^2

cos 2A = (7/8) - (9/25)

cos 2A = (35/40) - (32/40)

cos 2A = (3/40)

tan 2A = (2 tan A) / (1 - tan^2 A)

tan 2A = (2 * (3/4)) / (1 - (3/4)^2)

tan 2A = (3/2) / (1 - 9/16)

tan 2A = (3/2) / (7/16)

tan 2A = (3/2) * (16/7)

tan 2A = 24/7

So, the values are:

sin 2A = (3√7) / 20

cos 2A = 3/40

tan 2A = 24/7

Example 3: We aim to prove the identity:

3sinθ - 4sin^3θ cos^3θ - 3cosθ = tan^3θ

Solution:

We'll use multiple angle formulas to prove this identity. First, we'll express sin^3θ and cos^3θ in terms of sin3θ and cos3θ, and then we'll apply the formulas.

Multiple angle formulas state:

sin3θ = 3sinθ - 4sin^3θ

cos3θ = 4cos^3θ - 3cosθ

Now, we can rewrite the identity using these expressions:

3sinθ - 4(sin3θ)cosθ - 3cosθ = tan^3θ

Substituting the multiple angle formulas:

3sinθ - 4(3sinθ - 4sin^3θ)cosθ - 3cosθ = tan^3θ

Now, simplify the expression:

3sinθ - 12sinθ cosθ + 16sin^3θ cosθ - 3cosθ = tan^3θ

Factor out sinθ cosθ:

3sinθ(1 - 4cos^2θ + 16sin^2θ) - 3cosθ = tan^3θ

Now, use the Pythagorean identity sin^2θ + cos^2θ = 1:

3sinθ(1 - 4(1 - sin^2θ) + 16sin^2θ) - 3cosθ = tan^3θ

Simplify the expression inside the parentheses:

3sinθ(1 - 4 + 4sin^2θ + 16sin^2θ) - 3cosθ = tan^3θ

Combine like terms:

3sinθ(20sin^2θ - 3) - 3cosθ = tan^3θ

Now, factor out 3sinθ:

3sinθ(20sin^2θ - 3) - 3cosθ = 3sinθtan^3θ

Divide both sides by 3sinθ:

20sin^2θ - 3 - cosθ = tan^3θ

Now, use the Pythagorean identity sin^2θ = 1 - cos^2θ:

20(1 - cos^2θ) - 3 - cosθ = tan^3θ

Distribute the 20:

20 - 20cos^2θ - 3 - cosθ = tan^3θ

Combine like terms:

-20cos^2θ - cosθ + 17 = tan^3θ

Now, we have the identity:

-20cos^2θ - cosθ + 17 = tan^3θ

So, we've successfully proven the given identity using multiple-angle formulas.