Area of an Equilateral Triangle Formula: Derivations, Properties

Area of an Equilateral Triangle Formula: An equilateral triangle is a geometric shape with three equal sides and internal angles of 60° each. Below are some methods and derivations to  find out  the area of an equilateral triangle, you need to know the length of its sides. Now, we will explore three different methods for calculating this area.

• Derivation Area of  Equilateral Triangle  Through Basic Triangle Formula
• Derivation Through Rectangle Construction
• Derivation Through Trigonometry

Area of an Equilateral Triangle Formula

The area of an equilateral triangle (A) can be computed using the following formula:

Where:

A represents the area of the triangle.

a stands for the length of its sides.

Area of an Equilateral Triangle Formula Derivation Through Basic Triangle Formula

Begin with an equilateral triangle having a side length of "a" units.

Draw a perpendicular bisector from the top vertex to the base, forming a right-angled triangle with base "a" and height "h."

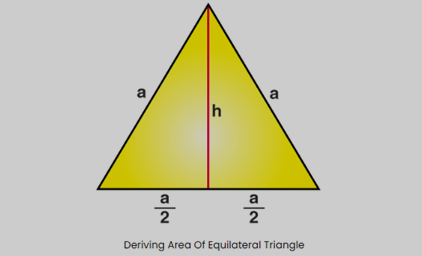
Now, we apply the Pythagorean Theorem:

a² = h² + (a/2)²

Solving for h:

h² = a² - (a²/4)

h² = (3a²)/4

h = (1/2)√3a

Now, Substitute the value of h into Area Formula

A = (1/2) × a × (1/2)√3a

A = (1/4)√3a²

Area of an Equilateral Triangle Formula Derivation Through Rectangle Construction

Start with an equilateral triangle that has side is “a”

Now, Draw a line from the top vertex to the midpoint of the base, That is dividing it into two equal halves.

Cut along the line and move one half to form a rectangle.

Now, the area of the equilateral triangle equals the area of the rectangle:

A = (1/2) × a × h

Using the Pythagoras Theorem as before, we find h = (1/2)√3a.

Now, Substitute the value of h into Area Formula

A = (1/2) × a × (1/2)√3a

A = (1/4)√3a²

Area of an Equilateral Triangle Formula Derivation Through Trigonometry

If two sides of an equilateral triangle are known, you can calculate the height using trigonometric functions:

h = b. Sin C = c. Sin A = a. Sin B

Now, area of ABC = ½ × a × (b . sin C) = ½ × b × (c . sin A) = ½ × c (a . sin B)

Now, for an equilateral triangle, A = B = C = 60°

And a = b = c

Area = ½ × a × (a . Sin 60°) = ½ × a ² × Sin 60° = ½ × a ² × √3/2

So, Area of Equilateral Triangle = (√3/4)a ²

Properties of Equilateral Triangles

• All sides of an equilateral triangle are equal.
• All internal angles are congruent and measure 60° each.
• The area of an equilateral triangle can be calculated using the methods mentioned above.
• The perimeter of an equilateral triangle is three times the length of its sides.
• The area formula for an equilateral triangle is A = (1/4)√3a², where "a" represents the side length.

Examples

Example 1: Find out the area of an equilateral triangle with a perimeter of 18 cm.

Solution:

Given: Perimeter of the equilateral triangle = 18 cm

Using the formula: Perimeter = 3a, where "a" is the side length.

Step 1: Determine the side length using the perimeter.

3a = 18

a = 6 cm

So, each side measures 6 cm.

Step 2: Compute the area of the equilateral triangle using the formula.

Area (A) = (√3/4) × a² sq units

= (√3/4) × (6)² cm²

= (36√3)/4 cm²

Hence, the area of the given equilateral triangle is (36√3)/4 cm².

Example 2: Find out  the area of an equilateral triangle with a side length of 20 cm.

Solution:

The equilateral triangle Area Formula is: A = (√3/4) × a²

Substituting the given side length:

Area (A) = (√3/4) × (20)² cm²

= (400√3)/4 cm²

= 25√3 cm²

Therefore, the area of the equilateral triangle with a 20 cm side length is 100√3 cm².

Example 3: Find out  the area of an equilateral triangle with a side length of 6.5 cm.

Solution:

Given: Side of the equilateral triangle (a) = 6.5 cm

Using the area formula:

Area (A) = (√3/4) × a² cm²

= (√3/4) × (6.5)² cm²

= (105.625√3)/4 cm²

≈ 40.90 cm² (rounded to two decimal places)

Hence, the area of the equilateral triangle with a 6.5 cm side length is approximately 40.90 cm².

Example 4: Find out the area of an equilateral triangle with a side length of 15.75 cm.

Solution:

Given: Side of the equilateral triangle (a) = 15.75 cm

Applying the area formula:

Area (A) = (√3/4) × a² cm²

= (√3/4) × (15.75)² cm²

= (370.21875√3)/4 cm²

≈ 134.96 cm² (rounded to two decimal places)

Thus, the area of the equilateral triangle with a side length of 15.75 cm is approximately 134.96 cm².