Atomic Formula: Definition, Significance, Principle, Equation

Atoms are matter's basic units, containing a nucleus with protons and neutrons, surrounded by electrons in specific energy shells, influencing elemental characteristics. This also includes the models for arranging fundamental particles in an atom.

Discovery of Fundamental Particles

Late 1800s cathode ray tube experiments suggested negative charge, leading to Thomson's postulation of electrons.

• Charge to Mass Ratio of an Electron: Thomson, utilizing electric and magnetic fields, gauged the deflection of these cathode rays, concluding the charge-to-mass ratio of electrons to be around − 1.76 × 10 ¹¹ C/kg
• Charge on the Electron: Few Years later, Robert A. Millikan, using his renowned oil drop method, juxtaposed gravitational and electric forces acting on charged oil droplets carried out an experiment. This enabled him to ascertain the electron's charge, pegging it at approximately − 1.6 × 10 ^{− 19} C.
• Discovery of Proton: Ernest Rutherford, in 1920, proposed the term "proton" for the positive entities in the atomic nucleus. His 1909 gold foil experiment revealed the atom's concentrated positive center.
• Discovery of Neutron: James Chadwick, in 1932, bombarded beryllium with alpha particles (α), leading to the emission of neutral radiation. This radiation, undeterred by electric or magnetic fields, was from neutrons, particles with a similar mass to protons (≈1.6726 × 10 ⁻²⁷ kg) but no charge.

J.J. Thomson's Atomic Model (Plum Pudding Model)

Proposed: 1904 Description: Thomson visualized the atom as a sphere of positive charge with electrons (like "plums") embedded throughout. It resembled a "plum pudding" or a "raisin bun," where the 'raisins' or 'plums' were the electrons. Key Values & Formulas: None specific to this model, but Thomson identified the electron's charge-to-mass ratio to be − 1.76 × 10 ¹¹ C/kg.

Rutherford's Atomic Model

Proposed: After his 1909 gold foil experiment. Description: Rutherford's experiment demonstrated that atoms have a tiny, positively charged nucleus at their center, where most of the atom's mass is concentrated. Electrons orbit the nucleus, and most of the atom is empty space.

Key Values & Formulas: He didn't specify the exact paths of electrons. His discovery led to the understanding that the atomic number (Z) represents the number of protons in the nucleus and, in a neutral atom, also the number of electrons.

Estimation of closest distance of approach (derivation) of α -particle:

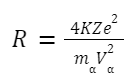
The radius of a nucleus:

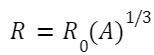
• Atomic Number (Z): The total count of protons in an atom's core. Its Importance: It gives every element its unique identity and is a key factor in determining its behavior in chemical reactions. In a balanced atom, it also matches the electron count.
• Defining Mass Number (A): The combined count of protons and neutrons in the center of an atom. Expression: A=Z+n, where n signifies the neutron count. Relevance: This offers a close estimate of the atomic weight in unified atomic mass units, given the near-equal mass of protons and neutrons.
• Understanding Isotopes: Variants of a single element that share a common atomic number but differ in the number of neutrons, leading to different mass numbers. Case in Point: Take hydrogen's variants - protium ( 1 H), deuterium ( 2 H), and tritium ( 3 H). All share an atomic number of 1 but have neutron counts of 0, 1, and 2 respectively.
• The Concept of Isobars: Atoms that share the same mass count but hail from different elements due to different atomic numbers. Noteworthy Aspect: They're part of different chemical families. Illustration: 40 Ca and 40 K are isobars with the identical mass count of 40. Yet, their atomic numbers differ: 20 for calcium and 19 for potassium.
• Electron Stability: According to classical physics, an electron moving in a circular orbit should release energy in the form of radiation. Thus, the electron should spiral into the nucleus, causing the atom to collapse. However, atoms are stable in reality.
• Electron's Fixed Orbit: Rutherford's model couldn't explain why electrons should move in particular orbits and not others.
• Atomic Spectra: The model failed to explain the discrete line spectra of atoms, especially the hydrogen spectrum, which displayed specific frequencies of light when excited.

Wave Nature of Electromagnetic Radiation

A. Max Planck's Quantum Theory: In 1900, Planck suggested that energy is quantized and can be emitted or absorbed in discrete units or quanta. This led to the concept of the "photon". E = hν Where: E is the energy of the photon ℎ h is Planck’s constant ν is the frequency of the radiation

B. Planck’s Quantum Theory:

C. Photoelectric Effect: Albert Einstein (1905) explained the phenomenon where electrons are ejected from the surface of metals when light falls on it. This could only be explained if light had a particle nature, leading to the dual nature of light. E = hν and

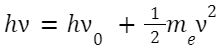
D. Wave-Particle Duality: Louis de Broglie in 1924 proposed that particles like electrons also have a wave nature. Wavelength associated with a moving particle: λ = h/p Where: p is the momentum of the particle

Also Check – Malic Acid Formula

Atomic Spectra

The spectra consist of continuous, emission, absorption, and band, each containing wavelengths without gaps. Continuous spectra observe atoms or molecules' transitions, absorption spectra observe specific frequencies, line spectra show discrete lines, and band spectra identify unknown elements.

Characteristics X-ray Spectrum:

When fast-moving electrons collide with a metal target in X-ray tubes, X-rays are produced. These X-rays consist of a continuous spectrum and some sharp, intense lines called characteristic lines. This is the characteristic X-ray spectrum of the metal.

Types of Series in the Hydrogen Spectrum: The different series in the hydrogen spectrum arise due to electron transitions between energy levels in the hydrogen atom. These series are:

Lyman Series: Transitions to the n=1 energy level. Ultraviolet region.

Balmer Series: Transitions to the n=2 energy level. Visible region. This is why we see distinct colored lines (e.g., red, blue-green) when hydrogen gas is excited.

Paschen Series: Transitions to the n=3 energy level. Infrared region. Brackett Series: Transitions to the n=4 energy level. Far infrared region.

Pfund Series: Transitions to the n=5 energy level. Far infrared region. Formula Related to the Hydrogen Spectrum: The wavelength of the emitted radiation for hydrogen transitions can be found using the formula derived from the Rydberg formula:

Where:  λ is the wavelength of the emitted radiation. R H ​ is the Rydberg constant for hydrogen (approximately 1.097 × 10 ⁷ m ^{− 1} ).  n ₁ and n ₂ ​ are the principal quantum numbers of the initial and final energy levels, with n ₂ ​>n ₁ .

Bohr's Model of the Hydrogen Atom

Postulates: Electrons move in circular orbits around the nucleus, with stationary states allowing no radiation. Radiation is emitted or absorbed when an electron jumps between orbits, with energy equal to the difference. This theory predicted hydrogen spectrum frequencies and introduced quantized energy levels.

Limitations: Only worked well for single-electron systems (like hydrogen or singly-ionized helium). Couldn't explain the Zeeman effect (splitting of spectral lines in a magnetic field) or the Stark effect (splitting in an electric field). Lacked a theoretical foundation until the development of quantum mechanics.

Formulas Related to Bohr's Model for the Hydrogen Atom:

• 
• 
• 
• 
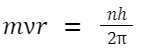
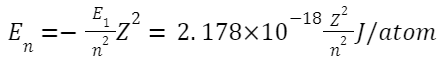
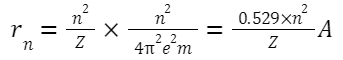
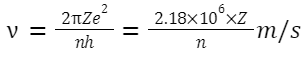
• The number of photons emitted by a H atom:
• 

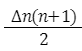
Limitations of Bohr's Model

• Applicability: Successful only for single-electron systems like hydrogen. Failed for multi-electron atoms.
• Zeeman & Stark Effects: Couldn't explain the splitting of spectral lines in magnetic (Zeeman) or electric (Stark) fields.
• Wave-Particle Duality: Ignored the wave nature of electrons introduced by de Broglie.

De-Broglie wavelength:

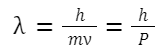
Also Read : Surface Chemistry Formula

Theoretical Foundation: Lacked a solid theoretical basis for its postulates. Fine Structure: Unable to explain the fine structure of spectral lines (multiple closely spaced lines).

Heisenberg Uncertainty Principle

Statement: The more precisely the position (Δx) of a particle is known, the less precisely its momentum (Δp) can be known, and vice versa. Mathematically: Δx×Δp≥ 4π h ​ Where ℎ is Planck's constant.

Implications: Nature imposes fundamental limits on quantum mechanics, challenging classical deterministic views and highlighting wave-particle duality and intrinsic limitations in our understanding of the quantum world.

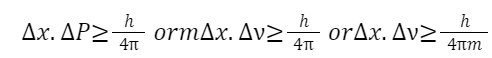
Also Check – Malic Acid Formula

Quantum Mechanical Model

Wave Function (Ψ): Represents the probability amplitude of a particle's position. The square of the absolute value of the wave function, ∣Ψ∣ ² , gives the probability density of finding the particle at a particular location.

Orbitals: These are regions in space where there's a high probability of finding an electron. Unlike Bohr's circular orbits, orbitals come in various shapes (s, p, d, f) and can contain up to two electrons with opposite spins.

Schrodinger Equation

Schrödinger's Equation is the fundamental equation in quantum mechanics, describing system changes over time. It involves the Hamiltonian operator H^, energy E, and wave function Ψ. The Pauli Exclusion Principle ensures unique addresses for electrons in an atom.

Quantum Numbers

They describe the complete properties of atomic orbitals and the electrons in those orbitals. There are four main quantum numbers:

1. Principal Quantum Number (n): Indicates the main energy level or shell of the atom. n=1,2,3,...

2. Azimuthal or Angular Momentum Quantum Number (l): Specifies the shape of the orbital. Values range from 0 to n−1 . Designations are s (l = 0), p(l = 1), d(l = 2), f(l = 3), and so on.

Orbital angular momentum of electron in any orbit:

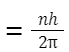
Azimuthal quantum number (l) = 0,1, …to (n-1)

Orbital angular momentum L =

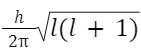
3. Magnetic Quantum Number (m l): This helps in determining the orientation of the orbital. Values range from −l to +l.

Number of orbitals in a subshell = 2l + 1

Maximum number of electrons in particular subshell 2 x (2l + 1)

4. Spin Quantum Number (m s): Helps in knowing the electron spin. Only two possible values: + 1/ 2 ​ or − 1 /2

Electronic Configuration Rules

• ​ Aufbau Principle: Electrons fill atomic orbitals in the ground state before occupying higher energy levels, like the 1s shell.
• Hund's Rule: Degenerate orbitals fill individually before pairing due to negatively charged electrons' repellence, making them energetically favorable.
• Pauli Exclusion Principle: Atomic electrons cannot have identical four-quad numbers, requiring orbitals with opposite spins and maximum electrons.