Physics Wallah

CBSE Class 11 Maths Notes Chapter 11 Conic Sections

Here, we have provided CBSE Class 11 Maths Notes Chapter 11 Conic Sections. Students can view these CBSE Class 11 Maths Notes Chapter 11 before exams for better understanding of the chapter.
authorImageAnanya Gupta7 May, 2024
Share

Share

CBSE Class 11 Maths Notes Chapter 11

CBSE Class 11 Maths Notes Chapter 11: In CBSE Class 11 Maths Notes Chapter 11: Conic Sections, you'll learn about different kinds of curves made by slicing a cone in different ways.

There are four main types: circles, ovals (like squished circles), U-shapes called parabolas, and curves called hyperbolas. You'll learn how to write equations for these curves and draw them on graphs. You'll also see how they're used in things like mapping out orbits in space, building bridges, and even making beautiful designs.

CBSE Class 11 Maths Notes Chapter 11 PDF

You can access the CBSE Class 11 Maths Notes for Chapter 11 on Conic Sections through the provided PDF link. By studying these notes, students can deepen their knowledge of these geometric shapes and their properties.

CBSE Class 11 Maths Notes Chapter 11 PDF

CBSE Class 11 Maths Notes Chapter 11 Conic Sections

The solutions for CBSE Class 11 Maths Notes Chapter 11 on Conic Sections are available below. With detailed explanations and examples, these solutions aim to aid students in understanding the properties and characteristics of conic sections. By referring to these notes, students can strengthen their grasp on the concepts and improve their problem-solving skills in mathematics.

Conic Sections

A conic section is the locus of a point that moves in a plane such that its distance from a fixed point, called the focus, is always in a constant ratio to its perpendicular distance from a fixed straight line, known as the directrix. This constant ratio is termed the eccentricity, denoted by 'e'. In the context of conic sections, the directrix and focus play crucial roles. The directrix is the fixed straight line, while the focus is the fixed point. A point where a conic intersects its axis is called a vertex. The axis of a conic section is the line passing through the focus and perpendicular to the directrix, which helps define the orientation and shape of the conic section.

General Equation of a conic: Focal directrix property

The general equation of a conic section can be derived from its focal-directrix property. This property states that for any point on the conic section, the distance from the point to the focus divided by the distance from the point to the directrix is equal to the eccentricity, denoted by 'e'.

Distinguishing various conics

The nature of conic section depends upon value of eccentricity as well as the position of the focus and the directrix. So, there are two different cases:

Case 1: When the Focus Lies on the Directrix.

In this case,

Δ ≡ a b c + 2 f g h − − a f 2 − − b g 2 − − c h 2 = 0 Δ≡ 𝑎𝑏𝑐 + 2𝑓𝑔ℎ −− 𝑎𝑓2 −− 𝑏𝑔2 −− 𝑐ℎ2 = 0

The general equation of a conic represents a pair of straight lines if:

e > 1 ≡ h 2 > a b 𝑒 > 1 ≡ ℎ2 > 𝑎𝑏

, Real and distinct lines intersecting at focus

e = 1 ≡ h 2 ⩾ a b 𝑒 = 1 ≡ ℎ2 ⩾ 𝑎𝑏

, Coincident lines

e < 1 ≡ h 2 < a b 𝑒 < 1 ≡ ℎ2 < 𝑎𝑏

, Imaginary lines

Case 2: When the Focus Does not Lies on the Directrix.

A parabola

An ellipse

A hyperbola

A rectangular hyperbola

Parabola

The definition of a parabola is a curve formed by the locus of a point, where its distance from a fixed point (called the focus) is equal to its perpendicular distance from a fixed straight line (called the directrix).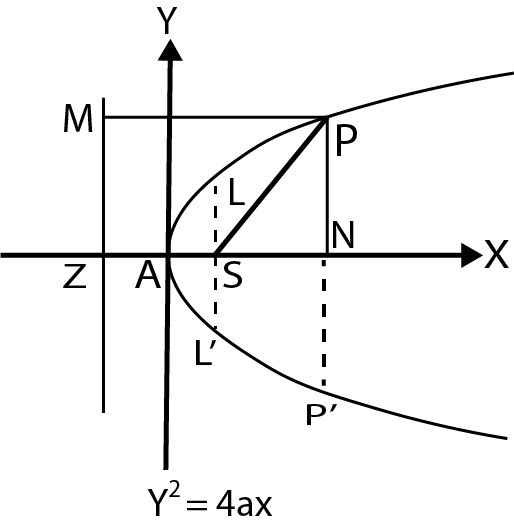 There are four standard forms of a parabola:
  1. 𝑦2=4𝑎𝑥
  2. 𝑦2=−4𝑎𝑥
  3. 𝑥2=4𝑎𝑦
  4. 𝑥2=−4𝑎𝑦
For the form 𝑦2=4𝑎𝑥 : (i) The vertex is at (0,0). (ii) The focus is at (a,0). (iii) The axis is the line y = 0. (iv) The directrix is the line x + a = 0. The focal distance is the distance of a point on the parabola from the focus. A chord passing through the focus is called a focal chord. A chord perpendicular to the axis of symmetry is called a double ordinate. The Latus Rectum is a double ordinate passing through the focus or a focal chord perpendicular to the axis of the parabola. For 𝑦2=4𝑎𝑥 : The length of the Latus Rectum is 4𝑎 , and its ends are at (a,2a) and (a,-2a). Perpendicular distance from the focus to the directrix is half the Latus Rectum. The vertex is the midpoint of the focus and the point where the directrix intersects the axis. Two parabolas are considered equal if they have the same Latus Rectum.

Position of a Point Relative to Parabola

Point ( x 1 , y 1 ) (𝑥1,𝑦1) lies inside, on or outside the parabola y 2 = 4 a x 𝑦2=4𝑎𝑥 depends upon the value of y 1 2 − 4 a x 1 𝑦12−4𝑎𝑥1 whether it is positive, negative or zero.

Line and Parabola:

The line y = m x + c 𝑦=𝑚𝑥+𝑐 meets parabola y 2 = 4 a x 𝑦2=4𝑎𝑥

at:

  • Two real points if a > m c 𝑎>𝑚𝑐
  • Two coincident points if a = m c 𝑎=𝑚𝑐
  • Two non real points if a < m c 𝑎<𝑚𝑐

Condition of Tangency is c = a m 𝑐=𝑎𝑚

Length of chord that line y = m x + c 𝑦=𝑚𝑥+𝑐 intercepts on parabola y 2 = 4 a x 𝑦2=4𝑎𝑥 is:

( 4 m 2 ) a ( 1 + m 2 ) ( a − m c ) −−−−−−−−−−−−−−−−√ (4𝑚2)𝑎(1+𝑚2)(𝑎−𝑚𝑐)

Parametric Representation:

( a t 2 , 2 a t ) (𝑎𝑡2,2𝑎𝑡) represents the co-ordinates of a point on the parabola is
y 2 = 4 a x 𝑦2=4𝑎𝑥 i.e. the equations x = a t 2 , y = 2 a t 𝑥=𝑎𝑡2,𝑦=2𝑎𝑡 at together represents the parabola with t being the parameter.
The equation of a chord joining t 1 & t 2 𝑡1&𝑡2 is 2 x − − ( t 1 + t 2 ) y + 2 a t 1 t 2 = 0. 2𝑥−−(𝑡1+ 𝑡2)𝑦 + 2 𝑎𝑡1𝑡2 = 0.

Auxiliary Circle

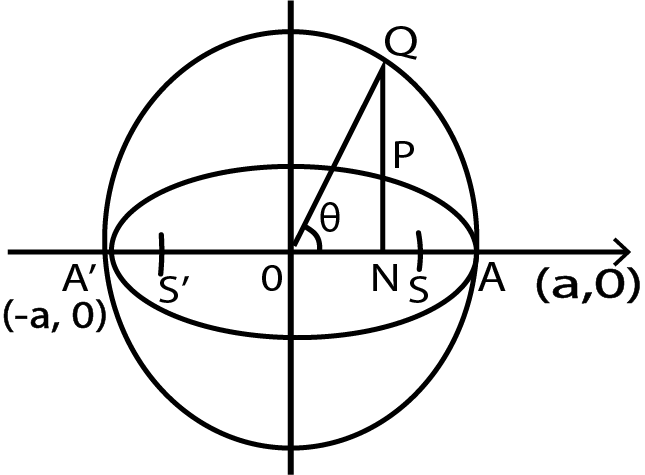A circle described on major axis as diameter is called the auxiliary circle. Let Q 𝑄 be a point on the auxiliary circle x 2 + y 2 = a 2 𝑥2+𝑦2=𝑎2 such that QP  produced is perpendicular to the x 𝑥 -axis, then P 𝑃 & Q 𝑄 are called as the Corresponding Points on the ellipse and the auxiliary circle respectively. θ 𝜃 is called the Eccentric angle of the point P P on the ellipse ( − π < θ ⩽ π ) (−𝜋<𝜃⩽𝜋) .

Pair of Tangents

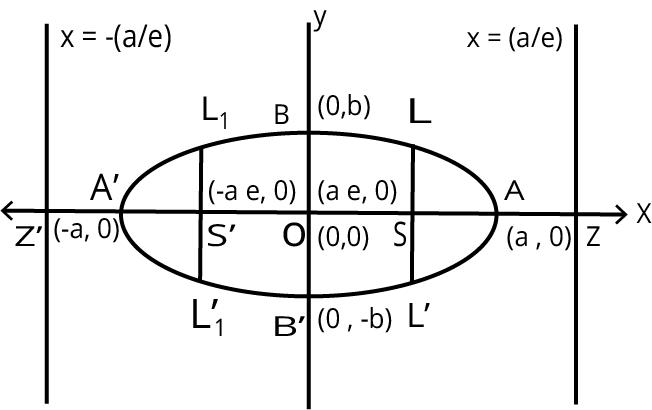
The equation to the pair of tangents which can be drawn from any point (x1,y1) to the parabola y2=4ax is given by: SS1=T2 where: S≡y2−4ax,S1=y21−4ax1,T≡yy1−2a(x+x1)

Director Circle

The director circle is defined as the locus of the point of intersection of perpendicular tangents to a curve. For the parabola 𝑦2=4𝑎𝑥 , its equation is 𝑥+𝑎=0 , which coincides with the parabola's own directrix.

Chord of Contact

The equation to the chord of contact of tangents drawn from a point 𝑃(𝑥1,𝑦1) is 𝑦𝑦1=2𝑎(𝑥+𝑥1) , denoted as 𝑇=0 . It's worth noting that the area of the triangle formed by the tangents from the point (𝑥1,𝑦1) and the chord of contact is given by (𝑦12−4𝑎𝑥1)322𝑎 . For a chord of the parabola 𝑦2=4𝑎𝑥 with a given middle point (𝑥1,𝑦1) , the equation is 𝑦−𝑦1=2𝑎𝑦1(𝑥−𝑥1) , which can also be expressed as 𝑇=𝑆1 .

Ellipse

Ellipse is a curved shape defined by its standard equation in terms of its principal axes along the coordinate axes: 𝑥2𝑎2+𝑦2𝑏2=1 where 𝑎>𝑏 , and 𝑏2=𝑎2(1−𝑒2) . The eccentricity 𝑒 of the ellipse is given by 𝑒=1−𝑏2𝑎2 , where 0<𝑒<1 . The ellipse has two foci 𝑆 and 𝑆′ located at (𝑎𝑒,0) and (−𝑎𝑒,0) respectively. The equations of the directrices are 𝑥=𝑎𝑒 and 𝑥=−𝑎𝑒 . The major axis is the line segment 𝐴′𝐴 , where 𝐴′ and 𝐴 are the vertices of the ellipse, and has a length of 2𝑎 . The minor axis is the line segment 𝐵′𝐵 , perpendicular to the major axis, with length 2𝑏 . The major and minor axes together are called the principal axis of the ellipse. The vertices of the ellipse are 𝐴′≡(−𝑎,0) and 𝐴≡(𝑎,0) . A focal chord is a chord that passes through a focus, while a double ordinate is a chord perpendicular to the major axis. The latus rectum is the focal chord perpendicular to the major axis. Its length is given by 2𝑏2𝑎=2𝑎(1−𝑒2)=2𝑒 , which is the distance from the focus to the corresponding directrix. The center of the ellipse is the point (0,0) , which bisects every chord of the ellipse drawn through it. If the equation of the ellipse is given as 𝑥2𝑎2+𝑦2𝑏2=1 without any further information, it is assumed that 𝑎>𝑏 . If 𝑏>𝑎 is given, then the y-axis becomes the major axis and the x-axis becomes the minor axis, and all other points and lines change accordingly.d
CBSE Class 11 Notes for Maths
Chapter 1 Sets Notes Chapter 2 Relations and Functions Notes
Chapter 3 Trigonometric Functions Notes Chapter 4 Principle of Mathematical Induction Notes
Chapter 5 Complex Numbers and Quadratic Equations Notes Chapter 6 Linear Inequalities Notes
Chapter 7 Permutations and Combinations Notes Chapter 8 Binomial Theorem Notes
Chapter 9 Sequences and Series Notes Chapter 10 Straight Lines Notes
Chapter 11 Conic Sections Notes Chapter 12 Introduction to Three Dimensional Geometry Notes
Chapter 13 Limits and Derivatives Notes Chapter 14 Mathematical Reasoning Notes
Chapter 15 Statistics Notes Chapter 16 Probability Notes

CBSE Class 11 Maths Notes Chapter 11 FAQs

What are conic sections?

Conic sections are curves formed by the intersection of a plane and a double-napped cone. The main types of conic sections are circles, ellipses, parabolas, and hyperbolas.

What are the properties of conic sections?

Conic sections have various properties related to their foci, directrices, eccentricities, vertices, and asymptotes, which depend on the type of conic section.

Is conic sections hard class 11?

Actually Conic Section is not hard , if you revise it regularly then it will be an easy and scoring chapter.

What are the 4 types of conic sections?

The four basic types of conics are parabolas, ellipses, circles, and hyperbolas.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.