Competitive Exams

IIT JEE, NEET, ESE, GATE, AE/JE, Olympiad

Only IAS

UPSC, State PSC

School Preparation

Foundation (Class 6-12), Commerce, Arts, CuriousJr (1st - 8th), Science, International Boards

Govt Exam

Judiciary, SSC, Defence, Teaching, JAIIB & CAIIB, BIHAR EXAMS WALLAH, UP Exams, Railway, Nursing Exams, Banking, WB Exams

UG & PG Entrance Exams

MBA, IPMAT, IIT JAM, LAW, CUET UG, UGC NET, GMAT, Design & Architecture, Pharma, CSIR NET, CUET PG, NEET PG

FINANCE

CA, CS, Finance Courses, ACCA

Others

Online Degrees

English Proficiency Test

IELTS, TOEFL

Agriculture

CBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives

Here, we have provided CBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives. Students can view these CBSE Class 11 Maths Notes Chapter 13 before exams for better understanding of the chapter.

Ananya Gupta9 May, 2024

CBSE Class 11 Maths Notes Chapter 13: In CBSE Class 11 Maths, Chapter 13 is all about Limits and Derivatives. These are important ideas in calculus, a branch of math used in many fields. In this chapter, students learn about limits, which show how values get closer to each other.

They also study derivatives, which help find rates of change and slopes of curves. By understanding these concepts, students can solve problems in math, science, and engineering. The notes for this chapter explain these ideas clearly, with examples to help students learn and practice. Mastering limits and derivatives in this chapter sets a strong foundation for future math studies and real-world applications.

CBSE Class 11 Maths Notes Chapter 13 PDF

You can access the CBSE Class 11 Maths Notes Chapter 13 on Limits and Derivatives in PDF format using the provided link. These notes cover important concepts such as limits and derivatives, which are fundamental in calculus. Understanding limits helps in approaching values or points, while derivatives are crucial for understanding rates of change and slopes of curves. By studying these notes, students can strengthen their understanding of calculus and prepare themselves for higher-level math studies.

CBSE Class 11 Maths Notes Chapter 13 PDF

CBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives

The solutions for CBSE Class 11 Maths Notes Chapter 13 on Limits and Derivatives are provided below, provide a detailed guide to understanding these fundamental concepts in calculus. Limits help us understand how values approach each other, while derivatives enable us to find rates of change and slopes of curves. With clear explanations and examples, these notes facilitate a deeper understanding of calculus principles, preparing students for further studies in mathematics and related fields. By mastering the concepts covered in this chapter, students can build a strong foundation for tackling more advanced topics in calculus and applying mathematical principles to real-world problems.

Limits

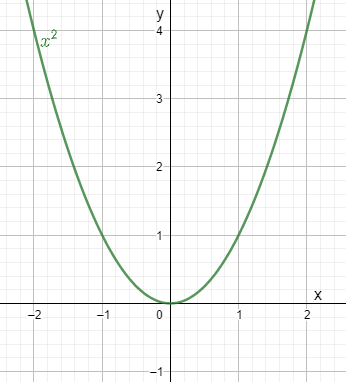Consider the function

f (x) = x^{2}

. When plotted, we see that as the value of

x

approaches 0, the value of

f (x)

also moves towards 0. In general, when

x

approaches a certain value

a

, and

f (x)

approaches a specific value

l

, then

l

is termed as the limit of the function

f (x)

, symbolized as

lim_{x \to a} f (x) = l

. Regardless of the limits, a function should assume a particular value at a given point

x = a

. There are two ways in which

x

can approach a number: from the left or from the right. This implies that all

x

values near

a

could be either less than

a

or greater than

a

. The right-hand limit represents the value of

f (x)

determined by

f (x)

values when

x

tends towards

a

from the right, denoted as

lim_{x \to a +} f (x)

. Similarly, the left-hand limit signifies the value of

f (x)

dictated by

f (x)

values when

x

approaches

a

from the left, expressed as

lim_{x \to a -} f (x)

. In our example, the right and left-hand limits differ. Hence, the limit of

f (x)

x

approaches zero does not exist, even though the function is defined at

x = 0

. If the right and left-hand limits converge to the same value, then that common value represents the limit and is denoted by

lim_{x \to a} f (x)

Algebra of limits

Theorem 1 states various properties of limits for two functions $f$ and $g$ :

If both

lim_{x \to a} f (x)

and

lim_{x \to a} g (x)

exist, then:

The limit of the sum of two functions is the sum of their limits: $lim_{x \to a} [f (x) + g (x)] = lim_{x \to a} f (x) + lim_{x \to a} g (x)$ .
The limit of the difference of two functions is the difference of their limits: $lim_{x \to a} [f (x) - g (x)] = lim_{x \to a} f (x) - lim_{x \to a} g (x)$ .
The limit of the product of two functions is the product of their limits: $lim_{x \to a} [f (x) \cdot g (x)] = lim_{x \to a} f (x) \cdot lim_{x \to a} g (x)$ .
The limit of the quotient of two functions is the quotient of their limits (provided the denominator is non-zero): $lim_{x \to a} g ( x ) f ( x ) = l i m ^{x \to a} g ( x ) l i m ^{x \to a} f ( x )$ .

In a special case when

g

is a constant function such that

g (x) = λ

for some real number

λ

The limit of a constant multiple of a function is equal to the constant multiplied by the limit of the function: $lim_{x \to a} [(λ \cdot f) (x)] = λ \cdot lim_{x \to a} f (x)$ .

Limits of polynomials and rational functions

A polynomial function

f

is one where

f (x)

is either a zero function or takes the form

f (x) = a_{0} + a_{1} x + a_{2} x^{2} + ... + a_{n} x^{n}

, where

a_{i}

are real numbers and

a_{n} \neq = 0

for some natural number

n

We know that

lim x \to a x = a

lim x \to a x 2 = lim x \to a (x . x) = lim x \to a x . lim x \to a x = a . a = a 2

Hence,

lim x \to a x n = a n

Let

f (x) = a 0 + a 1 x + a 2 x 2 + . . . + a n x n

be a polynomial function

lim x \to a f (x) = lim x \to a [a 0 + a 1 x + a 2 x 2 + . . . + a n x n]

$= lim_{x \to a} a_{0} + lim_{x \to a} a_{1} x + lim_{x \to a} a_{2} x^{2} + . . . + lim_{x \to a} a_{n} x^{n}$

$= a_{0} + a_{1} lim_{x \to a} x + a_{2} lim_{x \to a} x^{2} + . . . + a_{n} lim_{x \to a} x^{n}$

= a 0 + a 1 a + a 2 a 2 + . . . + a n a n

$= f (a)$

A rational function

f

is one where

f (x) = h ( x ) g ( x )

, and

g (x)

and

h (x)

are polynomials such that

h (x) \neq = 0

. Then,

lim_{x \to a} f (x) = lim_{x \to a} h ( x ) g ( x ) = l i m ^{x \to a} h ( x ) l i m ^{x \to a} g ( x ) = h ( a ) g ( a )

However, if

h (a) = 0

, there are two scenarios:

If $g (a) \neq = 0$ , the limit does not exist.
If $g (a) = 0$ , we have $g (x) = (x - a)^{k} g_{1} (x)$ and $h (x) = (x - a)^{l} h_{1} (x)$ , where $k$ is the maximum power of $(x - a)$ in $g (x)$ and $l$ is the maximum power of $(x - a)$ in $h (x)$ .
- If $k \geq l$ , then the limit is $0$ .
- If $k < l$ , the limit is not defined.

Theorem 2

For any positive integer $n$ , $lim_{x \to a} \frac{x^{n} - a^{n}}{x - a} = n a^{n - 1}$ .

The proof is shown below.

Dividing $(x^{n} - a^{n})$ by $(x - a)$ ,

$lim_{x \to a} \frac{x^{n} - a^{n}}{x - a} = lim_{x \to a} (x^{n - 1} + x^{n - 2} a + x^{n - 3} a^{2} + . . . + x a^{n - 2} + a^{n - 1})$

$= a^{n - 1} + a a^{n - 2} + . . . + a^{n - 2} (a) + a^{n - 1}$

$= a^{n - 1} + a^{n - 1} + . . . + a^{n - 1} + a^{n - 1} (n terms)$

$= n a^{n - 1}$

Limits of Trigonometric Functions

Theorem 3

Theorem 3 states that if

f

and

g

are two real-valued functions with the same domain, and

f (x) \leq g (x)

for all

x

in their domain, then if both

lim_{x \to a} f (x)

and

lim_{x \to a} g (x)

exist, then

lim_{x \to a} f (x) \leq lim_{x \to a} g (x)

Theorem 4

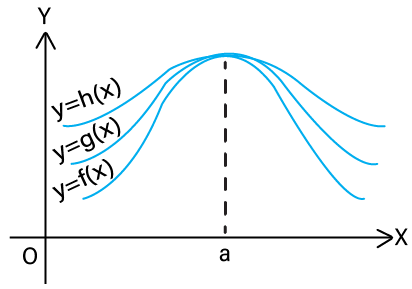The Sandwich Theorem, or Theorem 4, asserts that if three real functions

f (x)

g (x)

, and

h (x)

satisfy

f (x) \leq g (x) \leq h (x)

for all

x

in their common domain, and if

lim_{x \to a} f (x) = l = lim_{x \to a} h (x)

, then

lim_{x \to a} g (x) = l

. To prove that

cos (x) < x s i n ( x ) < 1

for

0 < ∣ x ∣ < 2 π

, it is observed that

sin (x)

lies between

cos (x)

and

tan (x)

. Since

0 < x < 2 π

sin (x)

is positive. Thus, dividing throughout by

sin (x)

s i n ( x ) 1 < s i n ( x ) x < c o s ( x ) 1

, leading to

cos (x) < x s i n ( x ) < 1

. Two important limits are given:

$lim_{x \to 0} x s i n ( x ) = 1$
$lim_{x \to 0} x 1 - c o s ( x ) = 0$

Derivatives

The derivative of a function at a given point within its domain of definition is a fundamental concept in calculus. Definition 1 states that if

f

is a real-valued function and

a

is a point in its domain, the derivative of

f

a

is defined as

lim_{h \to 0} h f ( a + h ) - f ( a )

, provided this limit exists. It is denoted as

f^{'} (a)

. Definition 2 defines the derivative of

f

x

lim_{h \to 0} h f ( x + h ) - f ( x )

where the limit exists. This definition is also known as the first principle of derivative. The derivative of a function

f (x)

with respect to

x

can be denoted as

f^{'} (x)

, represented as

d x d (f (x))

, or if

y = f (x)

, it is represented as

d x d y

. Another notation used is

D (f (x))

. Further, derivative of f at

x = a

is also denoted by

Moreover, the derivative of

f

x = a

can be denoted as

d x d f (x) ∣ ∣_{x = a}

d x df ∣ ∣_{x = a}

, or

(d x df)_{x = a}

For two functions

f

and

g

with defined derivatives in a common domain:

The derivative of their sum is the sum of their derivatives: $d x d [f (x) + g (x)] = d x d f (x) + d x d g (x)$ .
The derivative of their difference is the difference of their derivatives: $d x d [f (x) - g (x)] = d x d f (x) - d x d g (x)$ .
The product rule states that the derivative of the product of two functions is the first function's derivative times the second function plus the first function times the second function's derivative: $d x d [f (x) \cdot g (x)] = d x d f (x) \cdot g (x) + f (x) \cdot d x d g (x)$ .
The quotient rule states that the derivative of the quotient of two functions is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the square of the denominator: $d x d (g ( x ) f ( x )) = ( g ( x ) ) ^{2} d x d f ( x ) \cdot g ( x ) - f ( x ) \cdot d x d g ( x )$ .

Furthermore, the derivative of the function

f (x) = x

is a constant.

Theorem 6

Theorem 6 states that the derivative of a function

f (x) = x^{n}

n x^{n - 1}

for any positive integer

n

. Proof: By the definition of the derivative function, we have:

f^{'} (x) = lim_{h \to 0} h ( x + h ) ^{n} - x ^{n} = lim_{h \to 0} h h ( n x ^{n - 1} + \dots + h ^{n - 1} )

= lim_{h \to 0} (n x^{n - 1} + \dots + h^{n - 1}) = n x^{n - 1}

This can also be proved alternatively:

d x d (x^{n}) = d x d (x \cdot x^{n - 1})

= d x d (x) \cdot (x^{n - 1}) + x \cdot d x d (x^{n - 1})

(By the product rule)

= 1 \cdot x^{n - 1} + x \cdot ((n - 1) x^{n - 2})

(By induction hypothesis)

= x^{n - 1} + (n - 1) x^{n - 1} = n x^{n - 1}

Theorem 7

Theorem 7 states that for a polynomial function

f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0}

, where

a_{i}

s are real numbers and

a_{n} \neq = 0

, the derivative function is given by:

d x df ( x ) = n a_{n} x^{n - 1} + (n - 1) a_{n - 1} x^{n - 2} + \dots + 2 a_{2} x + a_{1}

Benefits Of CBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives

Complete Syllabus : The notes cover all the topics in Chapter 13 as per the CBSE syllabus, ensuring that students don't miss any important concepts.

Key Concepts : They provide a concise and clear explanation of key concepts such as limits, continuity, and derivatives, which are fundamental to understanding calculus.

Easy to Understand : The notes break down complex topics into simpler terms, making it easier for students to grasp difficult concepts..

Self-Study : With comprehensive notes, students can study on their own without much dependence on external help, boosting their confidence.

Concept Clarity : Clear understanding of fundamental concepts helps in building a strong foundation for higher studies.

CBSE Class 11 Notes for Maths
Chapter 1 Sets Notes	Chapter 2 Relations and Functions Notes
Chapter 3 Trigonometric Functions Notes	Chapter 4 Principle of Mathematical Induction Notes
Chapter 5 Complex Numbers and Quadratic Equations Notes	Chapter 6 Linear Inequalities Notes
Chapter 7 Permutations and Combinations Notes	Chapter 8 Binomial Theorem Notes
Chapter 9 Sequences and Series Notes	Chapter 10 Straight Lines Notes
Chapter 11 Conic Sections Notes	Chapter 12 Introduction to Three Dimensional Geometry Notes
Chapter 13 Limits and Derivatives Notes	Chapter 14 Mathematical Reasoning Notes
Chapter 15 Statistics Notes	Chapter 16 Probability Notes

CBSE Class 11 Maths Notes Chapter 13 FAQs

What are limits in calculus?

Limits in calculus define the behavior of a function as it approaches a certain point. It's a fundamental concept used to describe continuity, convergence, and divergence in mathematical functions.

How are limits calculated?

Limits are calculated by evaluating the behavior of a function as its input approaches a specific value. This involves analyzing the function's values as the input values get arbitrarily close to the desired value.

What is the derivative of a function?

The derivative of a function represents the rate at which the function is changing at any given point. Geometrically, it represents the slope of the tangent line to the graph of the function at that point.

What is the difference between a limit and a derivative?

A limit describes the behavior of a function as it approaches a specific point, while a derivative represents the rate of change of a function at a given point. Limits focus on the function's values, while derivatives focus on its rate of change.

🔥 Trending Blogs

CBSE Class 11 Sample Papers PDF with Solutions Download

CBSE Class 11 Biology Sample Paper 2025-26 PDF Download

CBSE Class 11 Maths Sample Paper, PDF Download

CBSE Sample Paper Class 11 Chemistry 2025-26 PDF Download Set Wise

CBSE 11 Class Physics Sample Paper 2025-26 PDF Download

Talk to a counsellorHave doubts? Our support team will be happy to assist you!

08448982616

008448982616

Check out these Related Articles

Join 15 Million students on the app today!

Live & recorded classes available at ease

Dashboard for progress tracking

Millions of practice questions at your fingertips

Free Learning Resources

PW Books

Notes (Class 10-12)

Class 10 Math's Notes

Class 10 Chemistry Notes

Class 10 Physics Notes

Class 10 Biology Notes

Aptitude & Reasoning

Class 10 Geography

Physics Class 11 Notes

Class 11 Chemistry Notes

Maths Notes Class 11

Zoology Class 11

Class 11 Botany Notes

Physics Class 12 notes

Chemistry Class 12

Maths Notes Class 12

Zoology class 12

Class 12th Botany Notes

PW Study Materials

Arjuna JEE Study Material

JEE 7 PYQs

JEE Mind Maps

Yakeen Study Material

NCERT Punch

Arjuna Neet Study Material

NEET PYQs

CBSE Sample Paper

CBSE Question Bank

Udaan For Class 10th Study Material

Notes (Class 6-9)

Class-6 Theory & Notes

Math's Notes for class 7

Science Notes for class 7

Class 8 Math Notes

Class 8 Chemistry Notes

Class 8 Physics Notes

Class 8 Biology Notes

Class 8 SST Notes

Class 9 Math's Notes

Class 9 Physics Notes

Class 9 Chemistry Notes

Class 9 Biology Notes

Ncert Solutions

NCERT Solutions For Class 6

NCERT Solutions For class 7

NCERT Solutions for class 8

NCERT Solutions for class 9

NCERT Solutions for class 10

NCERT Solutions for class 11

NCERT Solutions for Class 12

Govt Exams

Entrance Exams

Our Other Websites

Class 6th to 12th Online Courses

Class 12 Online Course

Class 11 Online Course

Class 10 Online Course

Class 9 Online Course

Class 8 Online Course

Govt Job Exams Courses

SSC Online Coaching

Bank Exam Online Coaching

TET Online Coaching

JAIIB & CAIIB Online Coaching

Bihar Exam Online Coaching

UPSC Coaching

UPSC Online Coaching

UPSC Offline & Hybrid Coaching

State PSC Online Coaching

UPPSC Online Coaching

BPSC Online Coaching

Defence Exam Coaching

NDA Online Coaching

CDS Online Coaching

AFCAT Online Coaching

Agniveer Online Coaching

Gate Exam Coaching

Civil Engineering Courses

Mechanical Engineering Courses

Formulas

Other Exams

Company Secretary Exam

Know about Physics Wallah

Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.

We Stand Out because

We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.

Our Key Focus Areas

Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.

What Makes Us Different

Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others