CBSE Class 11 Maths Notes Chapter 3 Trigonometric Functions
Neha Tanna8 May, 2024
Share
CBSE Class 11 Maths Notes Chapter 3: In mathematics for class eleven, one of the most crucial subjects is trigonometry functions. It describes how a right-angle triangle's sides and angles relate to one another. The Trigonometric Functions Class 11 Notes are a crucial study guide for students who want to understand trigonometric functions at a fundamental level.
The CBSE Class 11 Maths Notes Chapter 3 gives students an instant overview of all the subjects and formulas taught in the chapter, which helps them complete the trigonometry-based problems with greater confidence.CBSE Class 11 Maths Notes Chapter 3 Overview
The relationship between a triangle's sides and angles is the subject of trigonometry. It comes from the Greek terms "trigon" and "metron," which indicate the length of a triangle's sides. The measurement of a rotating line's rotation concerning a fixed line is called an angle. Depending on which way the angle is rotated, its value is either +ve or -ve [-ve for clockwise rotation and +ve for anti-clockwise rotation].CBSE Class 11 Maths Notes Chapter 3 PDF
For the benefit of the students, these Trigonometric Functions Class 11 Notes have been organized in a methodical manner. It is recommended that students consult these review materials as needed. With the use of the Class 11 Maths Notes Chapter 3 notes PDF, which has highly interactive information, students can efficiently prepare the entire chapter.CBSE Class 11 Maths Notes Chapter 3 PDF
CBSE Class 11 Maths Notes Chapter 3
The Meaning of Trigonometry
The Greek words "trigon" and "metron," which imply "measuring the slides of a triangle," are the origin of the word trigonometry. The original purpose of this topic's development was to address a geometrical issue with triangles. Surveyors to locate new areas, engineers, and sea captains employed trigonometry, among other applications.
These days, trigonometry is employed in a wide range of fields, including electric current design, ocean tidal height estimation, seismology research, etc.
You must have learned about trigonometric ratios of acute angles as a ratio of the triangle's sides in your previous studies. Trigonometric identities and applications of trigonometric ratios must also have been studied by you.
Because of this, this branch of mathematics was developed in antiquity to measure the six components, three sides, and three angles of a triangle.
There are many applications for time-trigonometric functions currently. In a right-angled triangle, the two fundamental functions are the sine and cosine of an angle; there are four other derivative functions.
Basic Trigonometric Identities
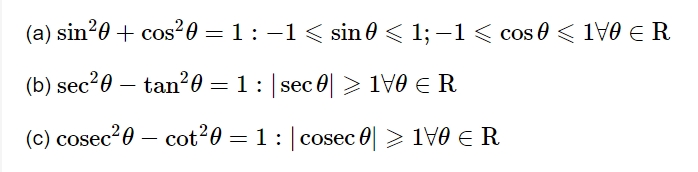
Trigonometric Ratios of Standard Angles
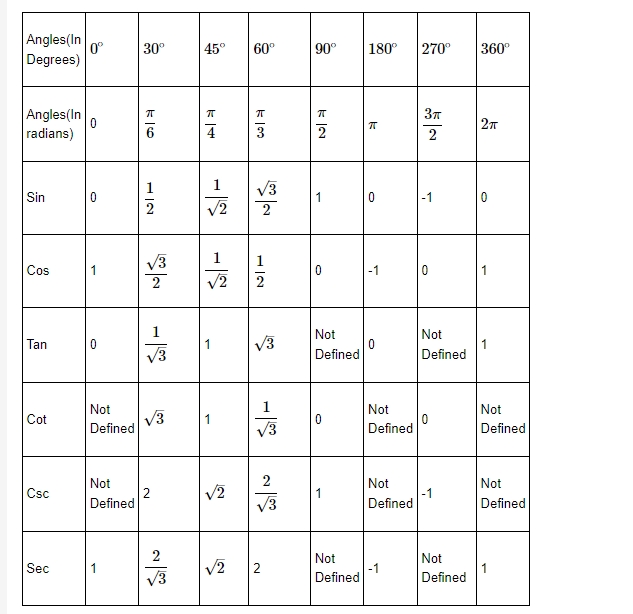
The relation between these trigonometric identities with the sides of the triangles can be given as follows:
-
Sine θ = = Opposite/Hypotenuse
-
Cos θ = = Adjacent/Hypotenuse
-
Tan θ = = Opposite/Adjacent
-
Cot θ = = Adjacent/Opposite
-
Cosec θ = Hypotenuse/Opposite
-
Sec θ = Hypotenuse/Adjacent
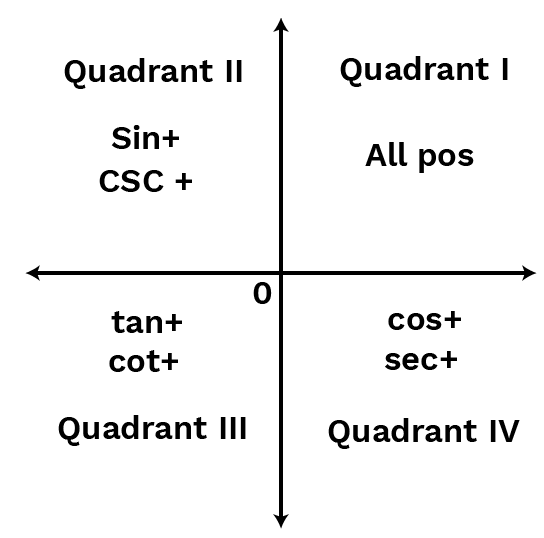
Trigonometric Ratios of Allied Angles
We might calculate the trigonometric ratios of angles of any value using the trigonometric ratio of allied angles.
1. Sin(–θ)=–Sinθ
2. Cos(–θ)=Cosθ
3. Tan(–θ)=–Tanθ
4. Sin(90–θ)=Cosθ
5. Cos(90–θ)=Sinθ
6. Tan(90–θ)=Cotθ
7. Sin(180–θ)=Sinθ
8. Cos(180–θ)=–Cosθ
9. Tan(180–θ)=–Tanθ
10. Sin(270–θ)=–Cosθ
11. Cos(270–θ)=–Sinθ
12. Tan(270–θ)=Cotθ
13. Sin(90+θ)=Cosθ
14. Cos(90+θ)=–Sinθ
15. Tan(90+θ)=–Cotθ
16. Sin(180+θ)=–Sinθ
17. Cos(180+θ)=–Cosθ
18. Tan(180+θ)=Tanθ
19. Sin(270+θ)=–Cosθ
20. Cos(270+θ)=Sinθ
21. Tan(270+θ)=–Cotθ
Trigonometric Functions of Sum or Difference of Two Angles
Multiple Angles and Half Angles
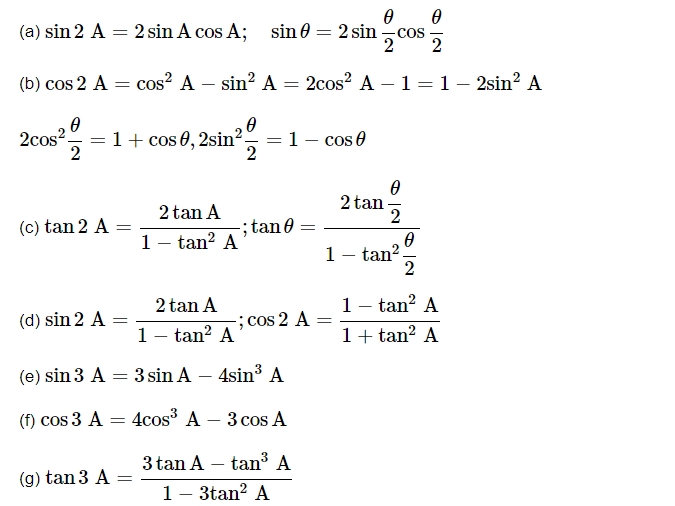
Transformation of Products into Sum or Difference of Sines & Cosines
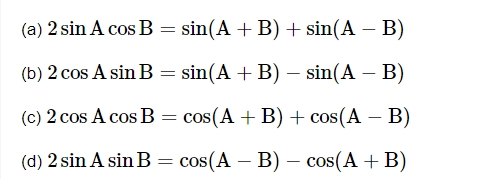
Factorization of the Sum or Difference of Two Sines or Cosines
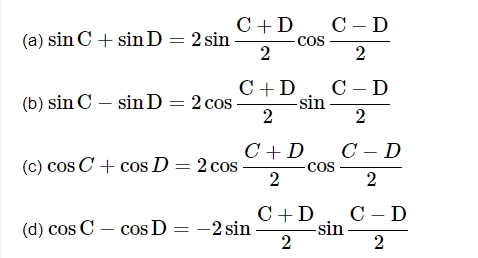
Important Trigonometric Ratios
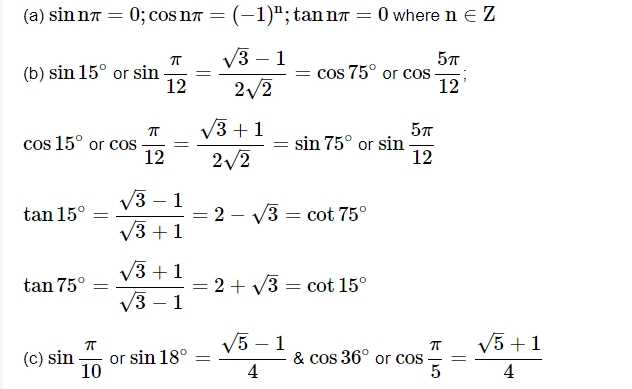
Conditional Identities
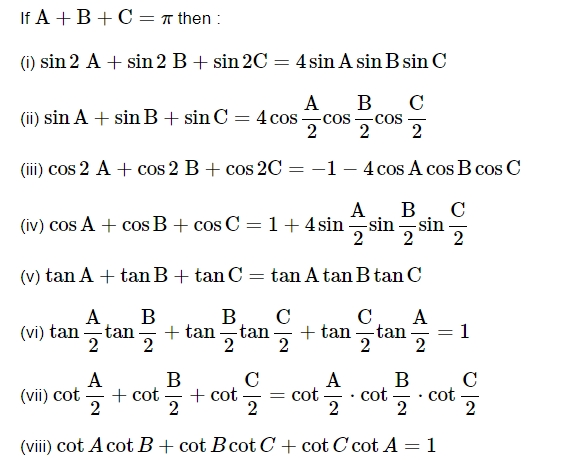
Range of Trigonometric Expression
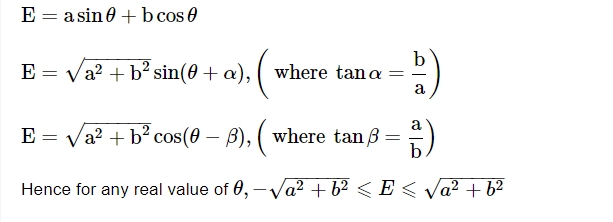
Trigonometric Functions in Different Domains and Ranges
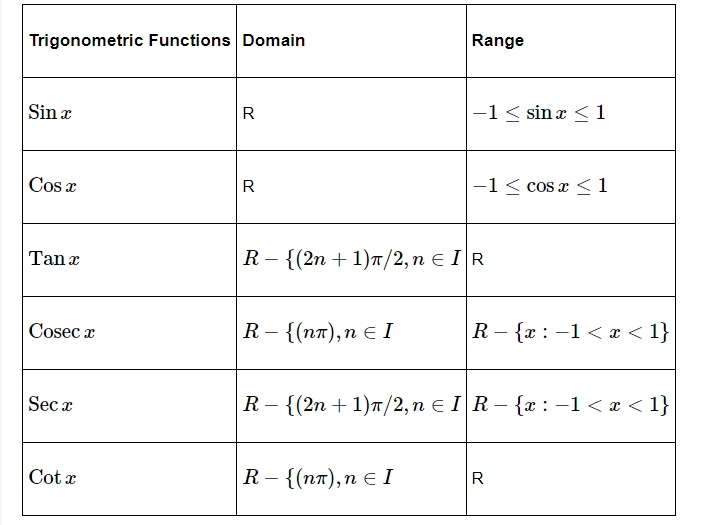
Graphs of Trigonometric Functions
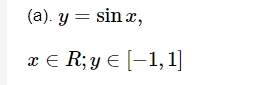
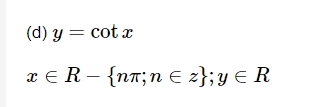
Steps to Solve Trigonometric Functions
The steps involved in solving trigonometric equations are as follows:Step 1: Break down the trigonometric equation into a single trigonometric ratio (sine or cos function, preferably).
Step 2: Use the ratio to factor the trigonometric polynomial that has been provided.
Step 3: After resolving each issue, write down the overall solution.
Take note:
1. Is considered an integer in this chapter unless otherwise indicated. 2. Unless the response is needed within a particular range or interval, a generic solution ought to be given. 3. α is considered to be the primary value of the angle. (The angle with the lowest numerical value is the primary value.)Benefits of CBSE Class 11 Maths Notes Chapter 3
The following is a discussion of several advantages provided by our Class 11 Maths Notes Chapter 3:- Notes on Maths for Class 11 A short and accurate summary of the material is given in material 3.
- Students can quickly and effectively review the key trigonometric function formulas and theorems with ease.
- Referring to the Class 11 Chapter 3 Mathematics notes will help students save valuable time.
- Just by looking at the revision notes, students can quickly remember all of the chapter's key ideas.
- Before the test, students can thoroughly review the subject of trigonometry by consulting Chapter 3 of the Class 11 Maths Notes.
CBSE Class 11 Maths Notes Chapter 3 FAQs
Which is the most scoring chapter in class 11 maths?
Is 11th maths difficult?
Is NCERT enough to score 100 in maths?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
