CBSE Class 11 Maths Notes Chapter 16 Probability PDF Download

CBSE Class 11 Maths Notes Chapter 16: In Chapter 16 of CBSE Class 11 Maths, you'll learn about probability, which is about figuring out the chances of something happening. You'll start by understanding basic terms like experiments, sample space, and events.

CBSE Class 11 Maths Notes Chapter 16 PDF Download

CBSE Class 11 Maths Notes Chapter 16 PDF

CBSE Class 11 Maths Notes Chapter 16 Probability

Probability Definition

Phrases and Ambiguity

"Probably" : This word suggests a likelihood or probability of something happening but doesn't specify how likely it is. For example, "It will probably rain tomorrow" indicates a higher chance of rain, but it's not guaranteed.

"Doubt" : When someone expresses doubt, they're unsure about the truth or validity of something. It implies skepticism or uncertainty. For instance, "I doubt he'll arrive on time" suggests uncertainty about the person's punctuality.

"Most Probably" : This phrase implies a high likelihood or probability of something happening, but it's not an absolute certainty. For example, "Based on the forecast, it will most probably be sunny tomorrow" suggests a strong chance of sunshine, but there's still a small possibility of other weather conditions.

"Chances" : When someone mentions "chances", they're referring to the probability or likelihood of an event occurring. For instance, "There's a good chance we'll win the game" indicates optimism about winning but acknowledges that it's not guaranteed.

Probability Calculation

Approaches to Probability

• Statistical Approach : Relies on observation and data collection from real-world events.
• Classical Approach : Assumes all outcomes are equally likely, often used for theoretical or simple scenarios.
• Axiomatic Method : Applies to real-life situations and has a strong connection to set theory, providing a rigorous framework for probability.

Random Experiments

• Random experiments have multiple possible outcomes.
• The outcome cannot be predicted in advance; it's uncertain until the experiment is conducted.

Outcomes

• An outcome is a possible result of a random experiment.
• For example, in a coin toss, getting heads or tails are two possible outcomes.

Sample Space

Definition : The sample space, denoted by the symbol $S$ , encompasses every conceivable outcome that could arise from a given experiment or situation.

Example : Let's consider the simple experiment of rolling a six-sided die. The sample space in this case would be the set $\{1,2,3,4,5,6\}$ , as these are all the possible outcomes of rolling the die.

Notation : The sample space is often represented using set notation, where each outcome is listed within braces {} and separated by commas. For example, if flipping a coin, the sample space would be $\{\text{Heads},\text{Tails}\}$ .

Sample Points : Each individual outcome within the sample space is called a "sample point". For instance, in the example of rolling a die, each number from 1 to 6 represents a sample point.

Importance : Understanding the sample space is crucial in probability theory because it forms the basis for calculating probabilities. By knowing all the possible outcomes, we can determine the likelihood of specific events occurring and make informed decisions based on that information.

Occurrence of an Event

Event Definition : An event is a collection of favorable outcomes or a specific scenario that we are interested in observing or analyzing within the context of a random experiment.

Occurrence : When the outcome of the experiment matches one of the outcomes within the event, we say that the event has occurred.

For example:

• Consider the event of rolling a dice and getting an even number. If you roll the dice and the outcome is 2, 4, or 6, then the event "rolling an even number" has occurred.
• Conversely, if the outcome is 1, 3, or 5, then the event hasn't occurred.

Types of Event

Impossible and Sure Events :

• Definition : An impossible event is one that cannot occur, while a sure event is one that is certain to occur.
• Representation : The impossible event is denoted by the empty set $\varnothing$ , while the sure event encompasses the entire sample space $S$ .
• Example : In the context of rolling a standard six-sided die, an impossible event would be rolling a number greater than 6, represented by $\varnothing$ . The sure event would be rolling any number between 1 and 6, as the die must land on one of these numbers.

Simple (or Elementary) Event :

• Definition : A simple event is one that consists of only one outcome or sample point from the sample space.
• Characteristics : Each simple event is unique and corresponds to a single outcome of the experiment.
• Example : Continuing with the example of rolling a six-sided die, a simple event could be rolling a specific number like 4. This event corresponds to only one outcome in the sample space.

Compound Event :

• Definition : A compound event is one that consists of multiple outcomes or sample points.
• Characteristics : Compound events involve combinations of simple events and can include more than one possible outcome.
• Example : In the context of rolling a six-sided die, a compound event could be rolling an even number (comprising the outcomes 2, 4, and 6). This event involves multiple outcomes and is therefore considered a compound event.

Algebra of Events

• Definition : The complementary event to event A, denoted by 𝐴′ A ′ or "not A", consists of all outcomes that are not in event A but are in the sample space.
• Representation : Mathematically, 𝐴′ A ′ can be expressed as 𝐴′=𝑆−𝐴 A ′ = S − A , where $S$ is the sample space.
• Example : Let's say event A is the event of rolling an odd number in a single throw of a fair six-sided die, which is {1, 3, 5}. Then, the complementary event to A, denoted as 𝐴′ A ′ , would be the event of rolling an even number, which is {2, 4, 6}.

• Definition : The event "A or B", denoted by $A\cup B$ , represents the union of events A and B. It consists of all outcomes that are in event A, in event B, or in both.
• Representation : Mathematically, $A\cup B$ can be expressed as $A\cup B=\{\omega :\omega \in A\text{or}\omega \in B\}$ .
• Example : If event A represents rolling an even number and event B represents rolling a prime number, then the event "A or B" represents rolling an even number, a prime number, or both.

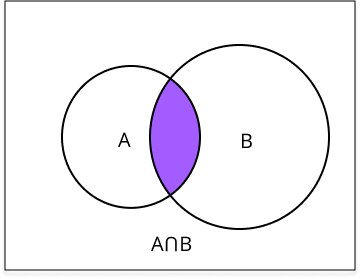
• Definition : The event "A and B", denoted by $A\cap B$ , represents the intersection of events A and B. It consists of all outcomes that are common to both events A and B.
• Representation : Mathematically, $A\cap B$ can be expressed as $A\cap B=\{\omega :\omega \in A\text{and}\omega \in B\}$ .
• Example : If event A represents rolling an even number and event B represents rolling a prime number, then the event "A and B" represents rolling an even prime number, which is only 2.

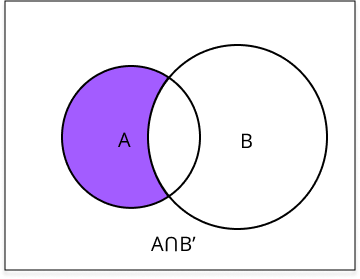
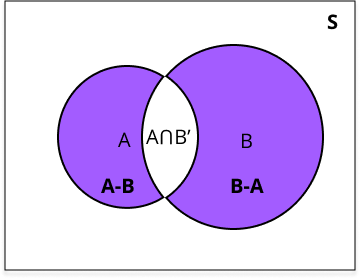
• Definition : The event "A but not B", denoted by $A-B$ or 𝐴∩𝐵′ A ∩ B ′ , consists of all outcomes that are in event A but not in event B.
• Representation : Mathematically, $A-B$ can be expressed as $A-B=\{\omega :\omega \in A\text{and}\omega \notin B\}$ .
• Example : If event A represents rolling an even number and event B represents rolling a prime number, then the event "A but not B" represents rolling an even number that is not prime, such as 6.

Mutually Exclusive Events

• Definition : Events A and B are said to be mutually exclusive if the occurrence of one of them prevents the occurrence of the other. In other words, they cannot happen at the same time.
• Example : When rolling a die, events A (even outcomes) and B (odd outcomes) are mutually exclusive because a roll cannot be both even and odd simultaneously.

Exhaustive Events

• Definition : Exhaustive events together cover all possible outcomes in the sample space. They leave no room for any other outcome to occur.
• Example : In the context of rolling a die, events A (even outcomes) and B (odd outcomes) together form exhaustive events because every outcome of rolling a die is either even or odd.

Axiomatic Approach to Probability

• Definition : The axiomatic approach to probability defines probability using axioms or fundamental rules. These axioms ensure that probability functions behave consistently and accurately.
• Axioms : i. Non-negativity: Probability of any event E is greater than or equal to zero. ii. Certainty: Probability of the entire sample space S is equal to 1. iii. Additivity: Probability of the union of mutually exclusive events E and F is the sum of their individual probabilities.
• Consequence : It follows from the third axiom that the probability of an impossible event is zero.

Probabilities of Equally Likely Outcomes

• Definition : When each outcome in the sample space is equally likely, the probability of an event is calculated as the ratio of the number of favorable outcomes to the total number of outcomes.
• Formula : 𝑃(𝐸)=𝑚𝑛 P ( E ) = n m ​ , where $m$ is the number of favorable outcomes and $n$ is the total number of outcomes.

Probability of the Event "A or B" :

• Formula : $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Probability of the Event "A and B" :

• Formula : $P(A\cap B)=P(A)+P(B)-P(A\cup B)$

Probability of the Event "Not A" :

• Formula : 𝑃(𝐴′)=1−𝑃(𝐴) P ( A ′ ) = 1 − P ( A )

Benefits of CBSE Class 11 Maths Notes Chapter 16 Probability

Foundation in Probability Theory : This chapter provides a solid foundation in probability theory, which is essential for understanding more advanced concepts in mathematics, statistics, and various other fields.

Real-World Applications : Probability theory has numerous applications in everyday life, science, finance, and technology. By studying this chapter, students gain insights into how probability concepts are used to make predictions, analyze data, and make informed decisions in diverse scenarios.

Problem-Solving Skills : Probability problems often involve critical thinking and logical reasoning. By practicing problems in this chapter, students enhance their problem-solving skills and develop a systematic approach to analyzing uncertain situations.

Decision Making : Understanding probability helps students make better decisions by quantifying uncertainties and assessing risks. This skill is valuable in various aspects of life, from personal finance to business management.

Preparation for Higher Education: Probability theory is a fundamental concept in mathematics and serves as a building block for higher-level courses in statistics, economics, engineering, and computer science. Mastering probability at the Class 11 level prepares students for more advanced studies in these fields.