
CBSE Class 11 Maths Notes Chapter 12: Introduction to Three Dimensional Geometry is very important topic for the exam. The concept of three-dimensional space, where points are located using three coordinates: (𝑥,𝑦,𝑧) . Through detailed explanations and examples, students learn about the Cartesian coordinate system in three dimensions and how to visualize points, lines, and planes in 3D space.
The CBSE Class 11 Maths Notes Chapter 12 gives students an instant overview of all the subjects and formulas taught in the chapter, which helps them complete the Dimensional Geometry-based problems with greater confidence.CBSE Class 11 Maths Notes Chapter 12 PDF
You can access the CBSE Class 11 Maths Notes for Chapter 12 on Introduction to Three Dimensional Geometry through the provided PDF link. This chapter teaches about working with objects and shapes in three-dimensional space. It covers topics like coordinates, distance, and direction. Understanding three-dimensional geometry is important for fields like engineering, architecture, and computer graphics. By using these notes, students can learn more about working with objects in three-dimensional space and improve their problem-solving skills.CBSE Class 11 Maths Notes Chapter 12 PDF
CBSE Class 11 Maths Notes Chapter 12 Introduction to Three Dimensional Geometry
Solutions for CBSE Class 11 Maths Notes Chapter 12 on Introduction to Three-Dimensional Geometry are available below. By using these solutions, students can deepen their understanding of three-dimensional concepts and improve their problem-solving skills. These notes serve as a valuable resource for mastering the principles of three-dimensional geometry.Coordinate Axes
Coordinate axes are imaginary lines that serve as reference lines in a coordinate system. In a three-dimensional coordinate system, there are three mutually perpendicular coordinate axes: the x-axis, the y-axis, and the z-axis. These axes intersect at a common point called the origin, often denoted as O. Three mutually perpendicular lines, denoted as OX, OY, and OZ, collectively form the coordinate axes.Coordinate Planes
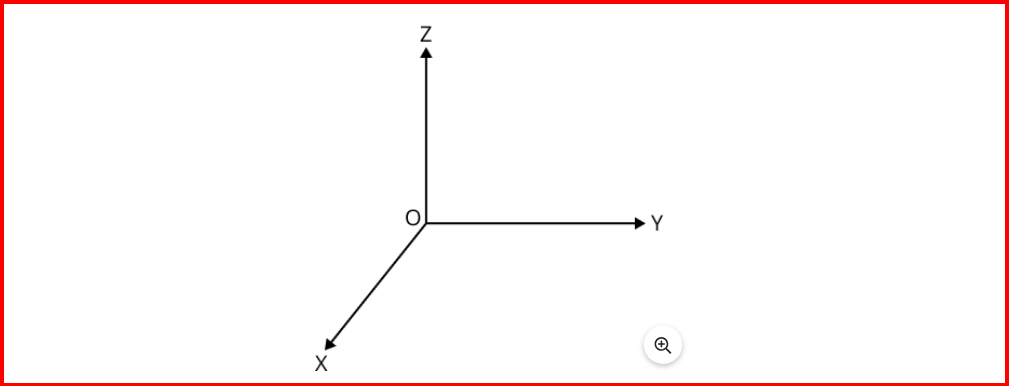
- The planes created by the coordinate axes are termed as coordinate planes.
- The XY plane is formed by the x and y axes.
- The YZ plane is formed by the y and z axes.
- The XZ plane is formed by the x and z axes.
Coordinates of a Point in Space
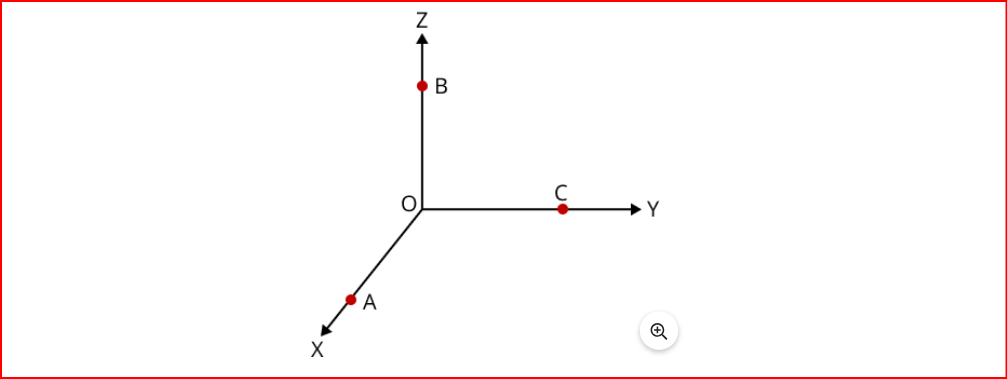
- The coordinates of the origin, labeled as point O, are (0,0,0).
- For any point A on the x-axis, its coordinates are (x,0,0).
- For any point B on the z-axis, its coordinates are (0,0,z).
- For any point C on the y-axis, its coordinates are (0,y,0).
- Points on the XY plane have coordinates (x,y,0), on the YZ plane have coordinates (0,y,z), and on the XZ plane have coordinates (x,0,z).
Octants
- A 3-dimensional coordinate system is divided into 8 sections known as octants.
- The sign convention for octants follows:
- Octant I: All coordinates are positive.
- Octant II: x-coordinate is negative, while y and z coordinates are positive.
- Octant III: x and y coordinates are negative, while z coordinate is positive.
- Octant IV: x-coordinate is positive, while y and z coordinates are negative.
- Octant V: x and z coordinates are positive, while y coordinate is negative.
- Octant VI: y-coordinate is positive, while x and z coordinates are negative.
- Octant VII: x, y, and z coordinates are negative.
- Octant VIII: y-coordinate is positive, while x and z coordinates are negative.
Understanding The Basics of Three Dimensional Geometry
According to experts, the introduction of three-dimensional geometry in mathematics aims to aid students in comprehending various types of figures and shapes. For instance, objects such as beds, chairs, tables, and kitchen utensils are all examples of three-dimensional geometric shapes. By studying this topic, students can better understand the spatial characteristics and properties of such objects, enhancing their grasp of geometry in practical contexts.The Coordinate System in Three Dimensional Geometry
The rectangular coordinate system, also known as the Cartesian coordinate system, is a fundamental tool in mathematics for representing points and shapes in two-dimensional and three-dimensional space. Comprising three perpendicular lines passing through a common point, it includes the x-axis, y-axis, and z-axis, converging at the observer or center, denoted by O.
This system facilitates measuring the distance covered by 3D objects. For instance, if an object's position coordinates are (3, -4, 5), it signifies movements of 3 units along the positive x-axis, 4 units along the negative y-axis, and 5 units along the positive z-axis.
Another crucial concept discussed is calculating distance from the origin, achievable via the Pythagorean theorem. For a point P (x, y, z), its distance from the origin (0, 0, 0) is given by √(x^2 + y^2 + z^2).
The distance between two points P (x1, y1, z1) and Q (x2, y2, z2) is determined by the formula √((x2−x1)^2 + (y2−y1)^2 + (z2−z1)^2).
Dividing a line segment between two points P (x1, y1, z1) and Q (x2, y2, z2) involves calculating the coordinates of the division point R using the ratio (m:n), expressed as R = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n), (mz2 + nz1) / (m + n)).
Projection in 3D space is explored, with the projection PQ of a line segment equal to AB cos θ, where θ represents the angle between AB and PQ or CD.
Direction Ratios Of A Line And Direction Cosine
CBSE Class 11 Maths Notes Chapter 12 FAQs
Why is three-dimensional geometry important?
Three-dimensional geometry is important as it helps us understand and analyze objects and shapes in three-dimensional space, which is applicable in various fields such as engineering, architecture, physics, and computer graphics.
What are direction cosines and direction ratios?
Direction cosines are the cosines of the angles that a line makes with the coordinate axes, while direction ratios are numbers that are proportional to the direction cosines of a line.
How can I calculate the distance between two points in three-dimensional space?
The distance between two points A(x1, y1, z1) and B(x2, y2, z2) in three-dimensional space can be calculated using the distance formula, which is √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2).
What is the section formula?
The section formula is used to find the coordinates of a point that divides a line segment into a given ratio internally or externally.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
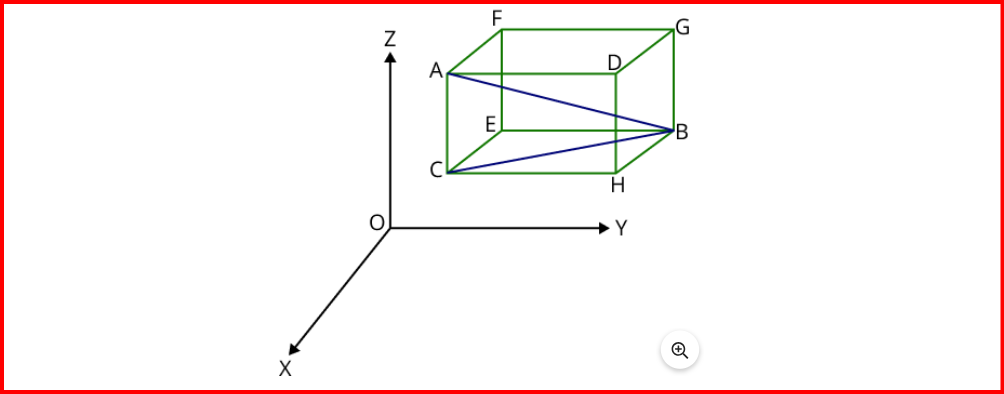 ii) The distance of any point (x1, y1, z1) from the origin is given by √(x1^2 + y1^2 + z1^2).
iii) According to the rule, the sum of two collinear points equals the third collinear point, applicable only when dealing with three collinear points A, B, and C. For instance, AB + BC = AC. The application of the distance formula helps determine collinearity among points.
ii) The distance of any point (x1, y1, z1) from the origin is given by √(x1^2 + y1^2 + z1^2).
iii) According to the rule, the sum of two collinear points equals the third collinear point, applicable only when dealing with three collinear points A, B, and C. For instance, AB + BC = AC. The application of the distance formula helps determine collinearity among points.
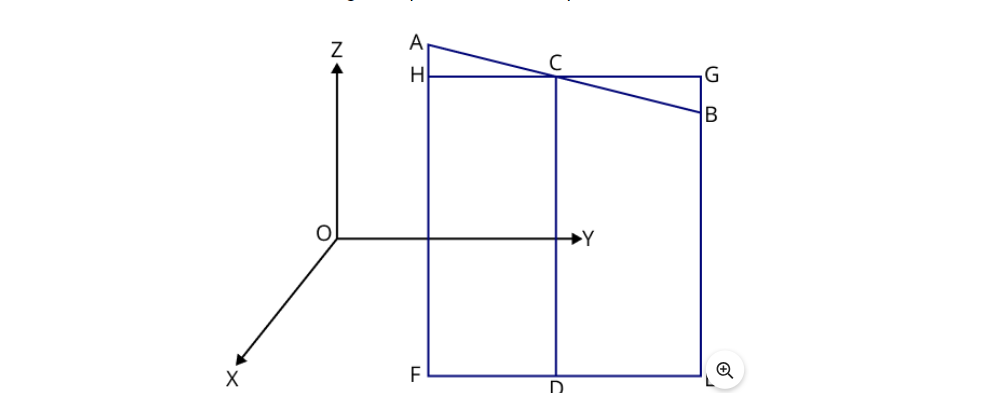 i) The Section Formula enables us to determine the internal division ratio of a line segment by a point.
ii) If point C divides the line segment AB internally, the ratio m:n in which AB is divided internally can be found using the section formula.
iii) Consider two points A(x1, y1, z1) and B(x2, y2, z2), with C(x, y, z) dividing the line segment AB internally in the ratio m:n.
iv) Perpendiculars are drawn from A, B, and C on the XY plane, such that AH||CD||BE. Additionally, line HG is drawn through point C, parallel to FE.
v) Quadrilaterals CDFH and DEGC are parallelograms based on the figure.
vi) ΔACH and ΔBCG are right-angled triangles with vertically opposite angles, thus similar. Hence, mn = AC/BC = AH/BG = AF - HF/GE - BE = AF - CD/CD - BE.
vii) Writing the corresponding coordinates, we derive mn = (z - z1)/(z2 - z) = (mz2 - mz)/(nz - nz1) = z(m + n)/(mz2 + nz1).
viii) Similarly, for other coordinates, x = (mx2 + nx1)/(m + n) and y = (my2 + ny1)/(m + n).
ix) Therefore, the required coordinates of the point dividing internally are (mx2 + nx1)/(m + n), (my2 + ny1)/(m + n), (mz2 + nz1)/(m + n).
x) For a midpoint, where m = 1 and n = 1, the coordinates of the point will be ((x2 + x1)/2, (y2 + y1)/2, (z2 + z1)/2).
i) The Section Formula enables us to determine the internal division ratio of a line segment by a point.
ii) If point C divides the line segment AB internally, the ratio m:n in which AB is divided internally can be found using the section formula.
iii) Consider two points A(x1, y1, z1) and B(x2, y2, z2), with C(x, y, z) dividing the line segment AB internally in the ratio m:n.
iv) Perpendiculars are drawn from A, B, and C on the XY plane, such that AH||CD||BE. Additionally, line HG is drawn through point C, parallel to FE.
v) Quadrilaterals CDFH and DEGC are parallelograms based on the figure.
vi) ΔACH and ΔBCG are right-angled triangles with vertically opposite angles, thus similar. Hence, mn = AC/BC = AH/BG = AF - HF/GE - BE = AF - CD/CD - BE.
vii) Writing the corresponding coordinates, we derive mn = (z - z1)/(z2 - z) = (mz2 - mz)/(nz - nz1) = z(m + n)/(mz2 + nz1).
viii) Similarly, for other coordinates, x = (mx2 + nx1)/(m + n) and y = (my2 + ny1)/(m + n).
ix) Therefore, the required coordinates of the point dividing internally are (mx2 + nx1)/(m + n), (my2 + ny1)/(m + n), (mz2 + nz1)/(m + n).
x) For a midpoint, where m = 1 and n = 1, the coordinates of the point will be ((x2 + x1)/2, (y2 + y1)/2, (z2 + z1)/2).









