Differentiation by Chain Rule Formula, Solved Examples

In the realm of differential calculus, the Chain Rule is a mathematical formula employed for determining the derivative of a composite function. If we have a function expressed as y = f(g(x)), then the chain rule stipulates that the instantaneous rate of change of function 'f' concerning 'g' and 'g' concerning 'x' results in the instantaneous rate of change of 'f' concerning 'x'. Consequently, the derivative of y can be expressed as y' = f'(g(x)) * g'(x). The chain rule stands as one of the fundamental principles in differentiation. This article aims to elucidate the chain rule formula through illustrated examples.

What is Chain Rule?

The principle employed to calculate the derivative of a composite function, such as cos 2x or log 2x, is commonly referred to as the chain rule. It's also known as the composite function rule. Importantly, the chain rule is specifically designed for composite functions. Thus, before delving into the chain rule formula, it's crucial to grasp the concept of a composite function and comprehend how to differentiate it.

Chain Rule Formula

The formula for the chain rule in the context of a composite function, where we have y = f(x), and f(x) is a composite function with x = g(t), is expressed as follows:

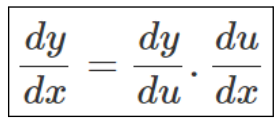
Standard Chain Rule Formula

This is the conventional representation of the chain rule formula for differentiation.

An alternative form of the chain rule is presented as:

y' = d/dx (f(g(x))) = f'(g(x)) * g'(x)

Composite Function For Chain Rule

A composite function is typically represented as:

(fog)(x) = f(g(x))

Suppose we have two differentiable functions, f(x) and g(x), and we want to find the derivative of their composite function f(g(x)). This derivative can be expressed as:

(fog)' = (f'og) * g'

Let's illustrate this with an example:

Consider f(x) = ex ² + 4 and g(x) = x ² + 4

So, f'(x) = 2x * ex ² , and g'(x) = 2x

Now, we can find the derivative of the composite function of f(x) and g(x) as follows:

(fog)' = (f'og) * g'

Let g(x) = k, which means f(x) = ek (where k = x ² + 4)

Therefore, (f'og) = ek, and g' = 2x

Hence, (fog)' = ek * 2x = ex ² + 4 * 2x

Also Check – Logarithm Formula

Chain Rule in Differentiation

Consider a real-valued function f, which is composed of two functions u and v, represented as:

f = v(u(x))

Now, suppose we assume u(x) = t. If both functions u and v are differentiable, and derivatives du/dx and dv/dt exist, then the composite function f(x) is also differentiable. This can be illustrated as follows:

Using Leibniz notation, we can express the differentiation of the given function as:

df/dx = (dv/dt) * (dt/dx)

As the name implies, the chain rule involves differentiating the terms in a sequential manner, starting from the outermost function and proceeding to the innermost function. In simpler terms, to find the derivative of a composite function at any point within its domain, begin by differentiating the outer function (i.e., the function that encloses another function) and then multiply it by the derivative of the inner function. This process yields the desired differentiation.

Also Check – Inverse Trigonometric Functions

Chain Rule for Partial Derivatives

The chain rule for total derivatives naturally extends to a chain rule for partial derivatives. When the total derivative exists, we can compute the partial derivative in the ith coordinate direction by taking the dot product of the ith basis vector's Jacobian matrix. Therefore, the chain rule for a function y = f(u) = (f1(u), …, fk(u)) and u = g(x) = (g1(x), …, gm(x)) can be expressed for partial derivatives as follows:

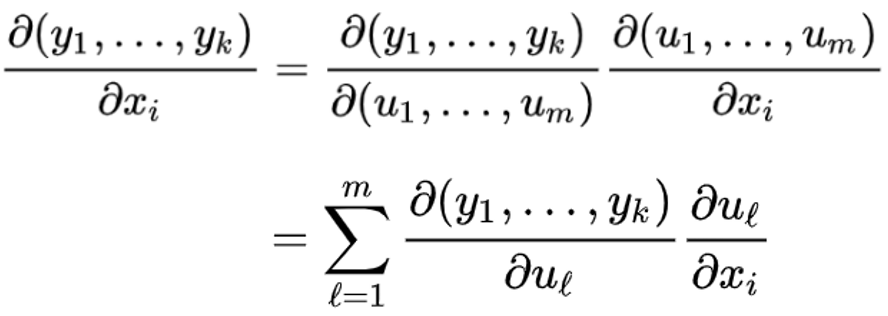
Also Check – Basics of Geometry Formula

Chain Rule Solved Examples

Example 1:

Let's find the derivative of the function f(x) = sin(2x ² – 6x).

Solution:

We can express the given function as a composite function as follows:

f(x) = sin(2x ² – 6x)

Let u(x) = 2x ² – 6x

And v(t) = sin(t)

So, we have t = u(x) = 2x ² – 6x

This implies f(x) = v(u(x))

Using the chain rule, we get:

df(x)/dx = (dv/dt) * (dt/dx)

Where,

dv/dt = d/dt (sin(t)) = cos(t)

dt/dx = d/dx [u(x)] = d/dx (2x ² – 6x) = 4x – 6

Therefore, df/dx = cos(t) * (4x – 6)

= cos(2x ² – 6x) * (4x – 6)

= (4x – 6) cos(2x ² – 6x)

Hence, the derivative of f(x) = sin(2x ² – 6x) is (4x – 6) cos(2x ² – 6x).