Introduction

Distance Formula

The distance between two points P(x1, y1) and Q(x ₂ , y ₂ ), is given

by .

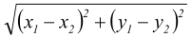Section Formula

If R divides the join of P(x1, y ₁ ) and Q(x ₂ , y ₂ ) in the ratio m : n (m, n > 0), then

x = 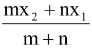y = 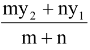(Internal Division)

and x = 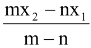y = 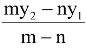(External Division)

Area of a Triangle

The area of a triangle ABC with vertices A(x ₁ , y ₁ ), B(x ₂ , y ₂ ) and C(x ₃ , y ₃ ) denoted conventionally by the symbol Δ is given by

Δ = 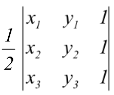= 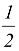{x1(y ₂ − y ₃ ) + x ² (y ₃ − y ₁ ) + x ³ (y ₁ − y ₂ )}

I. If one vertex say C(x ₃ , y ₃ ) is the origin (0, 0) then Δ = 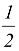|x ₁ y ₂ − x ₂ y1|.

II. If a ₁ x + b ₁ y + c ₁ = 0, a ₂ x + b ₂ y + c ₂ = 0 and a ₃ x + b ₃ y + c ₃ = 0 are the sides of a triangle then the area of a triangle is given by

Δ =

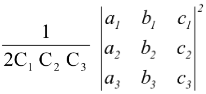
where C ₁ C ₂ C ₃ are the cofactors of c ₁ c ₂ c ₃ in the determinant.