Squares and Square Root Formula: The square root of a number is the reciprocal action of squaring that number. When we square a number, we multiply it by itself, resulting in a square value. Conversely, when we find the square root of a number, we determine a value that, when squared, yields the original number.
If 'a' represents the square root of 'b,' it signifies that a × a = b. The square of any given number is invariably positive, leading to each number having two square roots: one positive and one negative. For instance, 2 and -2 are both square roots of 4. However, conventionally, only the positive square root is denoted when referring to the square root of a number.
What is Square Root?
The square root of a number can be understood as the value that, when multiplied by itself, results in the original number. Within mathematics, squares and square roots hold a special place as exponents. Let's take the number 9 as an example. If we multiply 3 by itself, the outcome is 9, which can be represented as 3 × 3 or 32. In this case, the exponent is 2, termed as a square. Now, when the exponent is 1/2, it signifies the square root of the number. For instance, √n = n1/2, where "n" is a positive integer.
Also Check -
Introduction to Graph
Square Root Definition
The square root of a number corresponds to a value raised to the power of 1/2 for that number. Essentially, it's the number that, when multiplied by itself, results in the original number. This concept is symbolized by the '√' symbol. The symbol itself is referred to as a radical, while the numerical value beneath the radical is termed the radicand.
Download PDF Square Root Formula
Also Check -
Factorization Formula
How to Find Square Root?
To determine the square root of a number, we identify the number that, when squared, equals the given number. Finding the square root of a perfect square number is quite straightforward. Perfect squares refer to positive numbers that can be expressed as the result of multiplying an integer by itself. In essence, these numbers are represented by the power of 2 of an integer value.
There are four distinct methods available for calculating square roots:
Repeated Subtraction Method
Prime Factorization Method
Estimation Method
Long Division Method
It's important to note that the first three methods are particularly effective for perfect square numbers. On the other hand, the fourth method, which involves long division, can be applied to any number, whether it is a perfect square or not
A
lso Check -
Cubes and Cubes Roots Formula
Repeated Subtraction Method of Square Root
This method is quite straightforward. We repeatedly subtract consecutive odd numbers from the given number until we reach zero. The count of subtractions performed indicates the square root of the original number. This technique is applicable exclusively to perfect square numbers. Let's illustrate the process by finding the square root of 16 using this method.
Starting with 16:
Subtracting 1 gives 15.
Subtracting 3 from 15 gives 12.
Subtracting 5 from 12 gives 7.
Finally, subtracting 7 from 7 gives 0.
It's evident that we carried out 4 subtractions. Hence, √16 = 4.
Square Root by Prime Factorization Method
Prime factorization of a number involves expressing the number as a multiplication of its prime factors. When using the prime factorization method to calculate the square root of a given number, the following steps are followed:
Step 1: Break down the given number into its prime factors.
Step 2: Group these factors into pairs where each factor in a pair is identical.
Step 3: Select one factor from each pair.
Step 4: Multiply the factors selected in Step 3.
Step 5: The product obtained in Step 4 corresponds to the square root of the given number.
Let's apply this method to find the square root of 144.
For the number 144:
Step 1: Prime factorization of 144 = 2 × 2 × 2 × 3 × 3.
Step 2: Grouping the factors = (2 × 2) and (3 × 3).
Step 3: Selecting one factor from each pair = 2 and 3.
Step 4: Multiplying the selected factors = 2 × 3 = 6.
Step 5: The square root of 144 is 6.
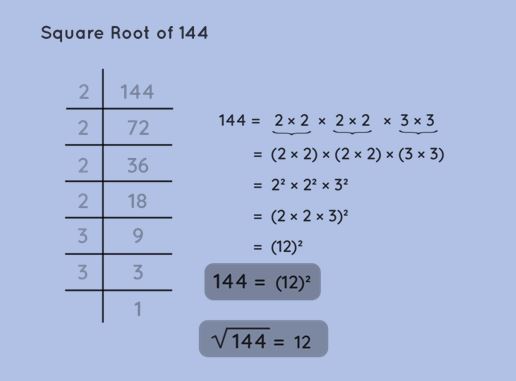
This method works when the given number is a perfect square number.
Also Check -
Comparing Quantities Formula
Finding Square Root by Estimation Method
Estimation and approximation involve making reasonable guesses about values to simplify calculations and render them more practical. This approach aids in estimating the square root of a given number. Let's apply this method to determine √15.
Begin by identifying the nearest perfect square numbers to 15, which are 9 and 16. It's known that √16 = 4 and √9 = 3. This indicates that √15 falls between 3 and 4. To refine this estimation, compare √15 with both 3.5 and 4. Calculating, 3.52 yields 12.25, while 42 equals 16. This suggests that √15 lies within the range of 3.5 and 4, closer to 4.
Further refinement can be achieved by examining the squares of 3.8 and 3.9. Computing 3.82 results in 14.44, and 3.92 gives 15.21. This confirms that √15 falls between 3.8 and 3.9. Continuing this process by evaluating between 3.85 and 3.9, we can deduce that √15 ≈ 3.872.
However, it's important to note that this method can be quite lengthy and time-consuming.
Also Check -
Quadrilaterals Formula
Calculating Square Root by Long Division Method
Long division is a technique employed to break down substantial numbers into manageable segments or steps, making the division process more approachable by breaking it into a series of simpler operations. Through this method, we can accurately determine the square root of any given number. Let's grasp the process of discovering the square root using the long division method through an example – finding the square root of 180.
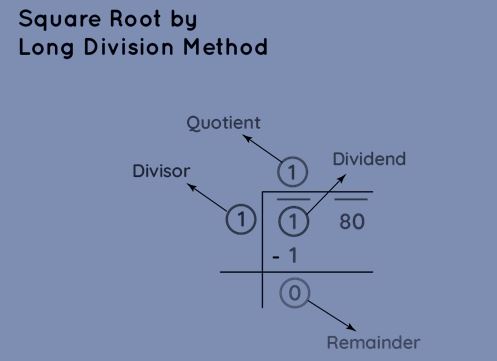
Step 1: Draw a bar over each pair of digits in the number, commencing from the units' place (rightmost side). In this case, we have two pairs: 1 and 80.
Step 2: Divide the initial pair on the left by the greatest number whose square is less than or equal to the value in that pair. This step initiates the process of finding the square root.
Step 3: Lower the number located below the following bar to the right of the remainder. Append the last digit of the quotient to the divisor. On the right of this sum, locate an appropriate number. Together with the outcome of the sum, it forms a new divisor for the new dividend that is brought down.
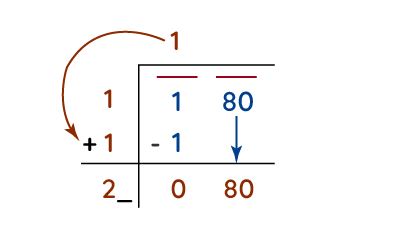
Step 4: The new figure in the quotient will share the same value as the one chosen for the divisor. The condition remains constant – it must be either less than or equal to the dividend.
Step 5: Proceed with this process, introducing a decimal point and appending pairs of zeros to the remainder.
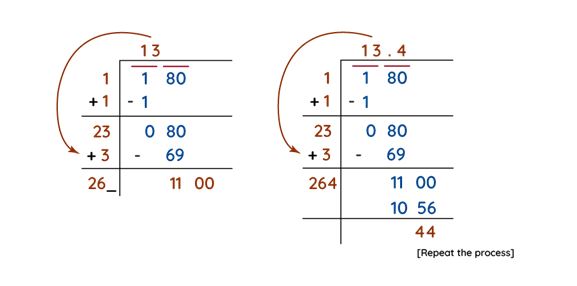
Step 6: The quotient thus obtained concludes the square root of the number. In the instance of the square root of 180, it approximates around 13.4. For greater precision, additional digits after the decimal point can be determined by replicating the same procedure.
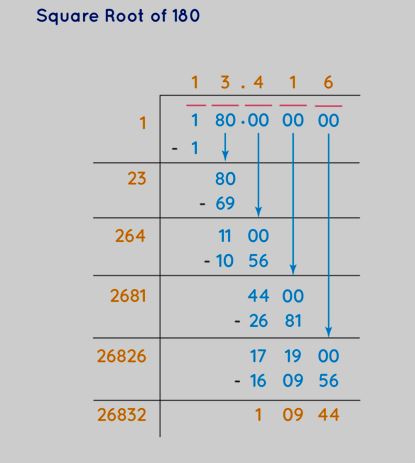
Ultimately, utilizing the long division method, we ascertain that the square root of 180 is roughly 13.4, and further digits can be extracted by repeating the process.
Square Root Table
The square root table is a compilation of numbers along with their corresponding square roots. This resource serves not only to determine square roots but also aids in calculating the squares of numbers. Below is a collection encompassing square roots for perfect square numbers as well as a selection of non-perfect square numbers spanning from 1 to 10.
|
Number
|
Square Root
|
|
1
|
1
|
|
2
|
1.414
|
|
3
|
1.732
|
|
4
|
2
|
|
5
|
2.236
|
|
6
|
2.449
|
|
7
|
2.646
|
|
8
|
2.828
|
|
9
|
3
|
|
10
|
3.162
|
Square Root Formula
The square root of a number is expressed with an exponent of 1/2. The square root formula is utilized to determine the square root of a given number. This formula is a subset of the exponent formula: n√x = x^(1/n), where n represents the exponent and, when n equals 2, it corresponds to the square root. Multiple methods can be employed to compute the square root, including approaches like prime factorization and more. For example, 9^(1/2) = √9 = √(3×3) = 3. Therefore, the formula for denoting the square root of a number is √x = x^(1/2).
Simplifying Square Root
To simplify a square root expression, it involves determining the prime factorization of the given number. In instances where a factor lacks a matching pair, it is retained within the square root symbol. Conversely, when pairs exist, one number is taken out of the square root from each pair. For instance, for √12 = √(2 × 2 × 3), this can be simplified to 2√3. This simplification rule aligns with √xy = √(x × y), where "x" and "y" denote positive integers.
Similar rules apply to fractions: √x/√y simplifies to √(x/y). For instance, √50/√10 can be simplified as √(50/10) = √5.
Square Root of a Negative Number
The square root of a negative number lacks a real-number solution, given that squares are either positive or zero. Nonetheless, the realm of complex numbers offers solutions for the square root of negative values. The primary square root of a negative number, -x, is expressed as: √(-x) = i√x, where "i" symbolizes the square root of -1.
For instance, consider the perfect square number 16. If we explore the square root of -16, we find that no real solution exists. However, √(-16) can be broken down as √16 × √(-1), resulting in 4i (since √(-1) equals i). In this context, "i" embodies the square root of -1, rendering 4i as a square root of -16.
Square of a Number
A number raised to the power of two (y^2) is denoted as the square of its base. For instance, 52 or 25 is recognized as the square of 5, while 82 or 64 is acknowledged as the square of 8. Determining the square of a number is a straightforward process of multiplying the number by itself. For example, 52 can be calculated as 5 × 5, yielding 25, and 82 as 8 × 8, resulting in 64. Whenever we compute the square of a whole number, the outcome corresponds to a perfect square. Notable examples of perfect squares include 4, 9, 16, 25, 36, 49, 64, and so forth. Importantly, the square of any number invariably produces a positive number
.
How to Find the Square of a Number?
The process of determining the square of a number entails multiplying the number by itself. When dealing with single-digit numbers, multiplication tables can be utilized to ascertain the square value. In scenarios involving two or more digits, we execute the multiplication of the number by itself, yielding the result. For instance, 9 × 9 equals 81, signifying the square of 9. Similarly, 3 × 3 equals 9, indicating the square of 3.
To express the square of a number, we employ an exponent of 2. For example, the square of 3 is notated as 32 and is pronounced as "3 squared." To exemplify:
42 equals 4 × 4, resulting in 16.
(-6)2 translates to -6 × -6, yielding 36.
(5/3)2 corresponds to the multiplication of 5/3 by itself, resulting in 25/9.
Squares and Square Roots
A profound interconnection exists between squares and square roots, with each being the reciprocal of the other. In mathematical terms, if x^2 = y, then it follows that x = √y. This relationship can be succinctly grasped through the following principles:
Square Removal: Eliminating the "square" term from one side of the equation results in the appearance of the square root on the other side. For instance, if we have 42 = 16, it translates to 4 = √16. This concept is often referred to as "taking the square root on both sides."
Square Root Removal: Conversely, when the "square root" term is removed from one side of the equation, we find the square term on the other side. For example, √25 = 5 corresponds to 25 = 52. This principle is known as "squaring on both sides."
