
ICSE Class 9 Maths Selina Solutions Chapter 11: Students can benefit from ICSE Class 9 Maths Selina Solutions Chapter 11 since they can help them achieve good exam scores. Complete, step-by-step explanations of all the problems found in ICSE Class 9 Maths Selina Solutions Chapter 11 are provided in the Selina Solutions provided on this page. The topic of inequality in triangles is covered in this chapter, which is a continuation of Chapter 10, Isosceles Triangle.
ICSE Class 9 Maths Selina Solutions Chapter 11 Overview
ICSE Class 9 Maths Selina Solutions Chapter 11 textbook covers the topic of Inequalities. Inequalities are mathematical expressions that compare two quantities or values. This chapter introduces students to different types of inequalities, including linear inequalities in one variable and their graphical representations on number lines. Students learn how to solve inequalities algebraically and graphically, understand concepts such as intervals, and open and closed intervals, and how to represent solutions to inequalities. Practical examples and exercises are provided to help students grasp the application of inequalities in real-world scenarios and strengthen their problem-solving skills in algebraic inequalities.ICSE Class 9 Maths Selina Solutions Chapter 11 PDF
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 11 in detail. This chapter will help you to clear all your doubts regarding the chapter Inequalities. Students are advised to prepare from these ICSE Class 9 Maths Selina Solutions Chapter 11 before the examinations to perform better.ICSE Class 9 Maths Selina Solutions Chapter 11 PDF
ICSE Class 9 Maths Selina Solutions Chapter 11 Inequalities
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 11 -1. From the following figure, prove that: AB > CD.
Solution:
In ∆ ABC, AB = AC[Given] Therefore, ∠ACB = ∠B [angles opposite to equal sides are equal] ∠B = 70 o [Given] ∠ACB = 70 o ………. (i) Now, ∠ACB +∠ACD = 180 o [ BCD is a straight line] 70 o + ∠ACD = 180 o ∠ACD = 110 o …………(ii) In ∆ ACD, ∠CAD + ∠ACD + ∠D = 180 o ∠CAD + 110 0 + ∠D = 180 o [From (ii)] ∠CAD + ∠ D = 70 o But ∠D = 40 o [Given] ∠CAD + 40 o = 70 o ∠CAD = 30 o ………………(iii) In ∆ ACD, ∠ACD = 110 o [From (ii)] ∠CAD = 30 o [From (iii)] ∠ D = 40 o [Given] ∠D > ∠CAD AC > CD [Greater angle has greater side opposite to it] Also, AB = AC[Given] Therefore, AB > CD.2. In a triangle PQR; QR = PR and ∠P = 36 o . Which is the largest side of the triangle?
Solution:
In ∆PQR, QR = PR[Given] Therefore ∠P = ∠Q [angles opposite to equal sides are equal] ∠P = 36 o [Given] ∠Q = 36 o In ∆ PQR, ∠P + ∠Q + ∠R = 180 o 36 o + 36 0 + ∠R = 180 o ∠R + 72 o = 180 o ∠R = 108 o Now, ∠R = 108 o ∠P = 36 o ∠Q = 36 o Since ∠R is the greatest, therefore, PQ is the largest side.3. If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
Solution:
The sum of any two sides of the triangle is always greater than the third side of the triangle. Third side < 13 + 8 = 21 cm. The difference between any two sides of the triangle is always less than the third side of the triangle. Third side > 13 – 8 = 5 cm. Therefore, the length of the third side is between 5 cm and 9 cm, respectively. The value of a = 5 cm and b = 21cm.4. In each of the following figures, write BC, AC, and CD in ascending order of their lengths.
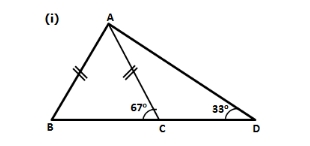
Solution:
In ∆ ABC, AB = AC ∠ABC = ∠ACB [angles opposite to equal sides are equal] ∠ABC = ∠ACB = 67 o ∠BAC = 180 o – ∠ABC – ∠ACB (angle sum property of triangle) ∠BAC = 180 o – 67 o – 67 o = 46 o Since ∠BAC < ∠ABC we have BC < AC ………… (1) Now, ∠ACD = 180 o – ∠ACB (linear pair) ∠ACD = 180 o – 67 o = 113 o In ∆ ACD, ∠CAD = 180 o – ∠ACD – ∠ADC ∠CAD = 180 o – 113 o – 33 o = 34 o Since ∠ADC < ∠CAD we have AC < CD … (2) From (1) and (2) we have BC < AC < CD In ∆ ABC, ∠BAC = ∠ABC BC < AC ……… (1) ∠ACB = 180 o – ∠ABC – ∠BAC ∠ACB = 180 o – 73 o – 47 o = 60 o Now, ∠ACD = 180 o – ∠ACB ∠ACD = 180 o – 60 o = 120 o In ∆ ACD, ∠ADC = 180 o – ∠ACD – ∠CAD ∠ADC = 180 o – 120 o – 31 o = 29 o Since ∠ADC < ∠CAD we have AC < CD … (2) From (1) and (2) we have BC < AC < CD5. Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
Solution:
In triangle BEC, ∠B + ∠BEC + ∠BCE = 180 0 ∠B = 65 0 [Given] ∠BEC = 90 0 [CE is perpendicular to AB] 65 0 + 90 0 + ∠BCE = 180 0 ∠BCE = 180 0 – 155 0 ∠BCE = 25 0 = ∠DCF …………(i) In triangle CDF, ∠DCF + ∠FDC + ∠CFD = 180 0 ∠DCF = 25 0 [From (i)] ∠FDC = 90 0 [AD is perpendicular to BC] 25 0 + 90 0 + ∠CFD = 180 0 ∠CFD = 180 0 – 115 0 ∠CFD = 65 06. D is a point inside BC of triangle ABC. If AD > AC, show that AB > AC.
Solution:
AD > AC (given) ∠C > ∠ADC …… (1) ∠ADC > ∠B + ∠BAC (exterior angle property) ∠ADC > ∠B ……… (2) From (1) and (2) we have ∠C > ∠ADC > ∠B ∠C > ∠B AB > AC7. In the following figure, ∠BAC = 60 o and ∠ABC = 65 o .
Prove that:
(i) CF > AF
(ii) DC > DF
Solution:
In ∆BEC, ∠B + ∠BEC + ∠BCE = 180 0 ∠B = 65 0 [Given] ∠BEC = 90 0 [CE is perpendicular to AB] 65 0 + 90 0 + ∠BCE = 180 0 ∠BCE = 180 0 – 155 0 ∠BCE = 25 0 = ∠DCF …………(i) In ∆CDF, ∠DCF + ∠FDC + ∠CFD = 180 0 ∠DCF = 25 0 [From (i)] ∠FDC = 90 0 [AD is perpendicular to BC] 25 0 + 90 0 + ∠CFD = 180 0 ∠CFD = 180 0 – 115 0 ∠CFD = 65 0 …………(ii) Now, ∠ AFC + ∠CFD = 180 0 [AFD is a straight line] ∠AFC + 65 0 = 180 0 ∠AFC = 115 0 ………(iii) In ∆ACE, ∠ACE + ∠CEA + ∠BAC = 180 0 ∠BAC = 60 0 [Given] ∠CEA = 90 0 [CE is perpendicular to AB] ∠ACE + 90 0 + 60 0 = 180 0 ∠ACE = 180 0 – 150 0 ∠ACE = 30 0 …………(iv) In ∆AFC, ∠AFC + ∠ACF + ∠FAC = 180 0 ∠AFC = 115 0 [From (iii)] ∠ACF = 30 0 [From (iv)] 115 0 + 30 0 + ∠FAC = 180 0 ∠FAC = 180 0 – 145 0 ∠FAC = 35 0 …………(v) In ∆AFC, ∠FAC = 35 0 [From (v)] ∠ACF = 30 0 [From (iv)] FAC > ACF CF > AF In ∆CDF, ∠DCF = 25 0 [From (i)] ∠CFD = 65 0 [From (ii)] CFD > DCF DC > DF8. In the following figure; AC = CD; ∠ BAD = 110 o and ∠ ACB = 74 o .
Prove that: BC > CD.
Solution:
∠ACB = 74 0 …..(i)[Given] ∠ACB + ∠ACD = 180 0 [BCD is a straight line] 74 0 + ∠ACD = 180 0 ∠ACD = 106 0 ……..(ii) In ∆ACD, ∠ACD + ∠ADC+ ∠CAD = 180 0 Given that AC = CD ∠ADC= ∠CAD 106 0 + ∠CAD + ∠CAD = 180 0 [From (ii)] 2∠CAD = 74 0 ∠CAD = 37 0 = ∠ADC………..(iii) Now, ∠BAD = 110 0 [Given] ∠BAC + ∠CAD = 110 0 ∠BAC + 37 0 = 110 0 ∠BAC = 73 0 ……..(iv) In ∆ABC, ∠B + ∠BAC+ ∠ACB = 180 0 ∠B + 73 0 + 74 0 = 180 0 [From (i) and (iv)] ∠B + 147 0 = 180 0 ∠B = 33 0 ………..(v) BAC > B BC > AC But AC = CD BC > CD9. From the following figure; prove that:
(i) AB > BD
(ii) AC > CD
(iii) AB + AC > BC
Solution:
(i) ∠ADC + ∠ADB = 180 0 [BDC is a straight line] ∠ADC = 90 0 [Given] 90 0 + ∠ADB = 180 0 ∠ADB = 90 0 …………(i) In ∆ADB, ∠ADB = 90 0 [From (i)] ∠B + ∠BAD = 90 0 Therefore, ∠B and ∠BAD are both acute, that is less than 90 0 . AB > BD ……. (ii)[Side opposite 90 0 angle is greater than side opposite acute angle] (ii) In ∆ADC, ADB = 90 0 ∠C + ∠DAC = 90 0 Therefore, ∠C and ∠DAC are both acute, that is less than 90 0 . AC > CD ……..(iii)[Side opposite 90 0 angle is greater than side opposite acute angle] Adding (ii) and (iii) AB + AC > BD + CD AB + AC > BC10. In a quadrilateral ABCD; prove that:
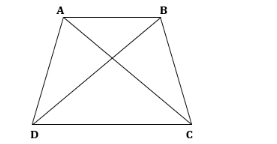
(i) AB+ BC + CD > DA
(ii) AB + BC + CD + DA > 2AC
(iii) AB + BC + CD + DA > 2BD
Solution:
Construction: Join AC and BD. (i) In ∆ABC, AB + BC > AC …. (i)[Sum of two sides is greater than the third side] In ∆ACD, AC + CD > DA …. (ii)[ Sum of two sides is greater than the third side] Adding (i) and (ii) AB + BC + AC + CD > AC + DA AB + BC + CD > AC + DA – AC AB + BC + CD > DA ……. (iii) (ii)In ∆ACD, CD + DA > AC …. (iv)[Sum of two sides is greater than the third side] Adding (i) and (iv) AB + BC + CD + DA > AC + AC AB + BC + CD + DA > 2AC (iii) In ∆ABD, AB + DA > BD …. (v)[Sum of two sides is greater than the third side] In ∆BCD, BC + CD > BD …. (vi)[Sum of two sides is greater than the third side] Adding (v) and (vi) AB + DA + BC + CD > BD + BD AB + DA + BC + CD > 2BD11. In the following figure, ABC is an equilateral triangle and P is any point in AC; prove that:
(i) BP > PA
(ii) BP > PC
Solution:
(i) In ∆ABC, AB = BC = CA [ABC is an equilateral triangle] ∠A = ∠B = ∠C ∠A = ∠B = ∠C = 180 o /3 ∠A = ∠B = ∠C = 60 o In ∆ABP, ∠A = 60 0 ∠ABP< 60 0 ∠A > ∠ABP BP > PA [Side opposite to greater side is greater] (ii) In ∆BPC, ∠C = 60 0 ∠CBP< 60 0 ∠C > ∠CBP BP > PC [Side opposite to greater side is greater]12. P is any point inside the triangle ABC. Prove that:
∠BPC > ∠BAC.
Solution:
Let ∠PBC = x and ∠PCB = y then, ∠BPC = 180 0 – (x + y) ………(i) Let ∠ABP = a and ∠ACP = b then, ∠BAC = 180 0 – (x + a) – (y + b) ∠BAC = 180 0 – (x + y) – (a + b) ∠BAC =∠BPC – (a + b) ∠BPC = ∠BAC + (a + b) ∠BPC > ∠BAC13. Prove that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
Solution:
We know that the exterior angle of a triangle is always greater than each of the interior opposite angles. In ∆ABD, ∠ADC > ∠B ……..(i) In ∆ABC, AB = AC ∠B = ∠C ….. (ii) From (i) and (ii) ∠ADC > ∠C (i) In ∆ADC, ∠ADC > ∠C AC > AD ………(iii) [side opposite to greater angle is greater] (ii) In ∆ABC, AB = AC AB > AD [ From (iii)]14. In the following diagram; AD = AB and AE bisect angle A. Prove that:
(i) BE = DE
(ii) ∠ABD > ∠C
Solution:
Construction: Join ED. In ∆AOB and ∆AOD, AB = AD [Given] AO = AO [Common] ∠BAO = ∠ DAO [AO is bisector of ∠A] Therefore ∆AOB ≅ ∆AOD [SAS criterion] Hence, BO = OD………(i) [c.p.c.t] ∠AOB = ∠AOD .……(ii) [c.p.c.t] ∠ABO = ∠ADO ∠ABD = ∠ADB ………(iii) [c.p.c.t] Now, ∠AOB = ∠DOE [Vertically opposite angles] ∠AOD = ∠BOE [Vertically opposite angles] ∠BOE = ∠DOE ……(iv) [From (ii)] (i) In ∆BOE and ∆DOE, BO = CD [From (i)] OE = OE [Common] ∠BOE = ∠DOE [From (iv)] Therefore ∆BOE ≅ ∆DOE [SAS criterion] Hence, BE = DE [c.p.c.t] (ii) In ∆BCD, ∠ADB = ∠C + ∠CBD [Ext. angle = sum of opp. int. angles] ∠ADB > ∠C ∠ABD > ∠C [From (iii)]15. The sides AB and AC of a triangle ABC are produced, and the bisectors of the external angles at B and C meet at P. Prove that if AB > AC, then PC > PB.
Solution:
In ∆ABC, AB > AC, ∠ABC < ∠ACB 180 0 – ∠ABC > 180 0 -∠ACB (180 0 – ∠ABC)/2 > (180 0 -∠ABC)/2 90 0 – ½ ∠ABC > 90 0 – ½ ∠ACB ∠CBP > ∠BCP (BP is bisector of ∠CBD and CP is bisector of ∠BCE) PC > PB (side opposite to greater angle is greater)16. In the following figure; AB is the largest side and BC is the smallest side of triangle ABC.
Write the angles x o , y o , and z o in ascending order of their values.
Solution:
Since AB is the largest side and BC is the smallest side of the triangle ABC AB > AC > BC 180 0 – Z 0 > 180 0 – y 0 -Z 0 > -y 0 > -x 0 Z 0 < y 0 < x 017. In quadrilateral ABCD, side AB is the longest, and side DC is the shortest.
Prove that:
(i) ∠C > ∠A
(ii) ∠D > ∠B.
Solution:
In the quadrilateral ABCD, Since AB is the longest side and DC is the shortest side. (i) ∠1 > ∠2 [AB > BC] ∠7 > ∠4 [AD > DC] ∠1 + ∠7 > ∠2 + ∠4 ∠C > ∠A (ii) ∠5 > ∠6[AB > AD] ∠3 > ∠8[BC > CD] ∠5 + ∠3 > ∠6 + ∠8 ∠D > ∠B18. In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that: ∠ADC is greater than ∠ADB.
Solution:
In ∆ADC, ∠ADB = ∠1 + ∠C………….(i) In ∆ADB, ∠ADC = ∠2 + ∠B……………..(ii) But AC > AB [Given] ∠B > ∠C Also given, ∠2 = ∠1 [AD is bisector of ∠A] ∠2 + ∠B > ∠1 + ∠C ……. (iii) From (i), (ii), and (iii) ∠ADC > ∠ADB19. In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies in BC produced (BC being produced through vertex C), prove that:
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
Solution:
We know that the bisector of the angle at the vertex of an isosceles triangle bisects the base at a right angle. Using Pythagoras theorem in ∆ AFB, AB 2 = AF 2 + BF 2 ………….. (i) In ∆ AFD, AD 2 = AF 2 + DF 2 ………….. (ii) We know ABC is an isosceles triangle and AB = AC AC 2 = AF 2 + BF 2 …….. (iii)b[ From (i)] Subtracting (ii) from (iii) AC 2 – AD 2 = AF 2 + BF 2 – AF 2 – DF 2 AC 2 – AD 2 = BF 2 – DF 2 Let 2DF = BF AC 2 – AD 2 = (2DF) 2 – DF 2 AC 2 – AD 2 = 4DF 2 – DF 2 AC 2 = AD 2 + 3DF 2 AC 2 > AD 2 AC > AD Similarly, AE > AC and AE > AD.20. Given: ED = EC
Prove: AB + AD > BC.
Solution:
In ∆CEB CE + EB > BC DE + EB > BC (CE = DE) DB > BC ……… (1) In ∆ADB, Ad + AB > BD AD + AB > BD > BC (from 1) AD + AB > BC21. In triangle ABC, AB > AC, and D is a point inside BC. Show that: AB > AD
Solution:
Given that AB > AC ∠C > ∠B ………. (1) In ∆ADC ∠ADB = ∠DAC + ∠C (exterior angle) ∠ADB > ∠C ∠ADB > ∠C > ∠B (from 1) ∠ADB > ∠B AB > ADBenefits of ICSE Class 9 Maths Selina Solutions Chapter 11
The Selina Solutions for ICSE Class 9 Maths Chapter 11 on Inequalities offers several benefits to students:Concept Clarity : The solutions provide clear explanations and step-by-step methods to solve different types of inequalities, ensuring students understand the underlying concepts thoroughly.
Variety of Problems : The chapter includes a variety of problems covering linear inequalities in one variable, graphical representations, and practical applications. This helps in developing a strong foundation and confidence in handling inequalities.
Real-World Applications : By solving practical problems, students can see how inequalities are applied in real-life situations, enhancing their ability to relate mathematical concepts to everyday scenarios.
Graphical Understanding : The chapter emphasizes graphical representations of inequalities on number lines, helping students visualize solutions and understand the relationship between inequalities and their graphical interpretations.
Preparation for Higher Classes : Mastering inequalities in Class 9 lays a solid groundwork for more complex topics in algebra and calculus that students will encounter in higher classes.
Problem-Solving Skills : Through practice problems and exercises, students improve their problem-solving skills and learn different approaches to tackle inequalities, thereby enhancing their overall mathematical proficiency.
Here at Physics Wallah we provide the Best CLASS 9 ONLINE COACHING to ease your exam preparation. Our class 9 online courses are taught by well-known instructors. We attempt to strengthen conceptual understanding and foster problem-solving abilities.ICSE Class 9 Maths Selina Solutions Chapter 11 FAQs
What are the inequalities of a triangle Class 9 ICSE?
Is triangle inequality strict?
Which one represents the triangular inequality?
What is double inequality?










