ICSE Class 9 Maths Selina Solutions Chapter 17 Circle
Neha Tanna12 Jul, 2024
Share
ICSE Class 9 Maths Selina Solutions Chapter 17: Students can benefit from ICSE Class 9 Maths Selina Solutions Chapter 17 since they can help them achieve good exam scores. The Class 9 Selina Textbook's Chapter 17, Circles, has all of the problems that are covered in detail, step-by-step, in the Selina Solutions.
These ICSE Class 9 Maths Selina Solutions Chapter 17, which outline the entire process of problem-solving, were created by our subject matter specialists. Students will be able to get all of their questions about "Circles" answered by comprehending the ideas presented in Selina Solutions for Class 9 Mathematics.ICSE Class 9 Maths Selina Solutions Chapter 17 Overview
ICSE Class 9 Maths Selina Solutions for Chapter 17 on Circles offer a detailed exploration of circle geometry, including key concepts such as the properties of tangents, chords, and sectors. The chapter emphasizes theorems related to angles, lengths, and areas associated with circles. ICSE Class 9 Maths Selina Solutions Chapter 17 Circle are structured to provide step-by-step guidance, helping students grasp the fundamental properties of circles, solve diverse problems, and prepare effectively for exams. This ICSE Class 9 Maths Selina Solutions Chapter 17 Circle is crucial for building a solid foundation in geometry, essential for advanced mathematical studies.ICSE Class 9 Maths Selina Solutions Chapter 17 PDF
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 17 in detail. This chapter will help you to clear all your doubts regarding the chapter Inequalities. Students are advised to prepare from these ICSE Class 9 Maths Selina Solutions Chapter 17 before the examinations to perform better.ICSE Class 9 Maths Selina Solutions Chapter 17 PDF
ICSE Class 9 Maths Selina Solutions Chapter 17 Circle
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 17 -1. A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
Solution:
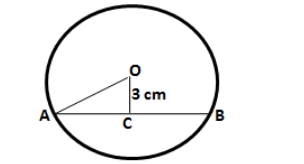
Consider AB as the chord and O as the centre of the circle. Take OC as the perpendicular drawn from the centre O to AB. Here, the perpendicular to a chord, from the centre of a circle, bisects the chord. So, AC = CB = 3 cm In △ OCA, OA 2 = OC 2 + AC 2 [Using Pythagoras Theorem] Substituting the values OC 2 = 5 2 – 3 2 OC 2 = 16 So we get OC = 4 cm2. A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of a circle.
Solution:
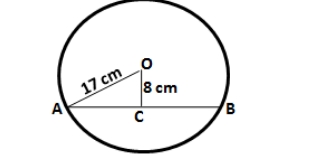
Consider AB as the chord and O as the centre of the circle. Take OC as the perpendicular drawn from the centre O to AB. Here, the perpendicular to a chord, from the centre of a circle, bisects the chord. So, AB = 8 cm We know that AC = CB = AB/2 Substituting the value of AB AC = CB = 8/2 AC = CB = 4 cm In △ OCA, OA 2 = OC 2 + AC 2 [Using Pythagoras Theorem] Substituting the values OA 2 = 4 2 + 3 2 OA = 25 So we get OA = 5 cm Therefore, radius of the circle is 5 cm.3. The radius of a circle is 17.0 cm and the length of perpendicular is drawn from its center to a chord is 8.0 cm. Calculate the length of the chord.
Solution:
Consider AB as the chord and O as the centre of the circle. Take OC as the perpendicular drawn from the centre O to AB. Here, the perpendicular to a chord, from the centre of a circle, bisects the chord. So, AC = CB In △ OCA, OA 2 = OC 2 + AC 2 [Using Pythagoras Theorem] Substituting the values AC 2 = 17 2 – 8 2 AC = 225 So we get AC = 15 cm AB = 2 AC = 2 × 15 = 30 cm4. A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
Solution:
Consider AB as the chord of length 24 cm and O as the centre of the circle. Take OC as the perpendicular drawn from the centre O to AB. Here, the perpendicular to a chord, from the centre of a circle, bisects the chord. So, AC = CB = 12 cm In △ OCA, OA 2 = OC 2 + AC 2 [Using Pythagoras Theorem] Substituting the values OA 2 = 5 2 + 12 2 OA = 169 So we get OA = 13 cm Therefore, radius of the circle is 13 cm. Consider A’B’ as the new chord at a distance of 12 cm from the centre. (OA’) 2 = (OC’) 2 + (A’C’) 2 Substituting the values (A’C’) 2 = 13 2 – 12 2 (A’C’) 2 = 25 A’C’ = 5 cm Length of the new chord = 2 × 5 = 10 cm5. In the following figure, AD is a straight line. OP ⊥ AD and O is the centre of both circles. If OA = 34 cm, OB = 20 cm and OP = 16 cm; find the length of AB.
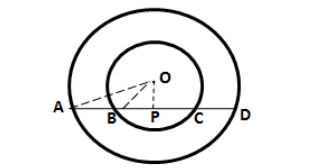In the inner circle, BC is the chord and OP ⊥ BC
Here, the perpendicular to a chord, from the centre of a circle, bisects the chord.
So, BP = PC
In △ OBP,
OB
2
= OP
2
+ BP
2
[Using Pythagoras Theorem]
Substituting the values
BP
2
= 20
2
– 16
2
BP
2
= 144
So we get
BP = 12 cm
In the outer circle, AD is the chord and OP ⊥ AD
Here, the perpendicular to a chord, from the centre of a circle, bisects the chord.
So, AP = PD
In △ OAP,
OA
2
= OP
2
+ AP
2
[Using Pythagoras Theorem]
Substituting the values
AP
2
= 34
2
– 16
2
AP
2
= 900
So we get
AP = 30 cm
Here, AB = AP – BP = 30 – 12 = 18 cm.
ICSE Class 9 Maths Selina Solutions Chapter 17 Exercise 17B
1. The figure shows two concentric circles and AD is a chord of larger circle. Prove that: AB = CD.
Draw OP ⊥ AD So OP bisects AD [Perpendicular drawn from the centre of a circle to a chord bisects it.] AP = PD ……… (i) BC is a chord for the inner circle and OP ⊥ BC So OP bisects BC [Perpendicular drawn from the centre of a circle to a chord bisects it.] BP = PC ………. (ii) By subtracting equation (ii) from (i), AP – BP = PD – PC AB = CD2. A straight line is drawn cutting two equal circles and passing through the midpoint M of the line joining their centres O and O’.
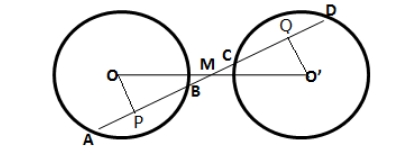
Prove that chords AB and CD, which are intercepted by the two circles are equal.
Solution:
Given – A straight line AD intersects two circles of equal radii at A, B, C and D. Line joining the centres OO’ intersect AD at M M is the midpoint of OO’ To prove – AB = CD. Construction – From the centre O, draw OP ⊥ AB and from O’ draw O’Q ⊥ CD. Proof – In △ OMP and △ O’MQ, ∠ OMP = ∠ O’MQ [vertically opposite angles] ∠ OPM = ∠ O’QM [each = 90 0 ] OM = O’M [given] By AAS criterion of congruence, △ OMP ≅ △ O’MP OP = O’Q [c.p.c.t] Here, two chords of a circle or equal circles which are equidistant from the centre are equal. AB = CD.3. M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that:
(i) ∠ BMN = ∠ DNM,
(ii) ∠ AMN = ∠ CNM.
Solution:
Draw OM ⊥ AB and ON ⊥ CD So OM bisects AB and ON bisects CD [Perpendicular drawn from the centre of a circle to a chord bisects it.] BM = ½ AB = ½ CD = DN ……..(1) In △ OMB, OM 2 = OB 2 + BM 2 [Using Pythagoras Theorem] We can write it as OM 2 = OD 2 – DN 2 [using equation (1)] OM 2 = ON 2 OM = ON So we get ∠ OMN = ∠ ONM ……. (2) [Angles opposite to the equal sides are equal] (i) ∠ OMB = ∠ OND [both 90 0 ] By subtracting (2) from above ∠ BMN = ∠ DNM (ii) ∠ OMA = ∠ ONC [both 90 0 ] By adding (2) to above ∠ AMN = ∠ CNM4. In the following figure: P and Q are the points of intersection of two circles with centres O and O’. If straight lines APB and CQD are parallel to OO’. Prove that
(i) OO’ = ½ AB
(ii) AB = CD
Solution:
Draw OM and ON perpendicular on AB and OM’ and O’N’ perpendicular on CD. So OM, O’N, OM’ and O’N’ bisect AP, PB, CQ and QD respectively [Perpendicular drawn from the centre of a circle to a chord bisects it.] MP = ½ AP, PN = ½ BP, M’Q = ½ CQ, QN’ = ½ QD We know that OO’ = MN = MP + PN = ½ (AP + BP) = ½ AB ……. (i) OO’ = M’N’ = M’Q + QN’ = ½ (CQ + QD) = ½ CD …… (ii) Equating (i) and (ii) AB = CD5. Two equal chords AB and CD of a circle with centre O, intersect each other at a point P inside the circle. Prove that:
(i) AP = CP
(ii) BP = DP
Solution:
Draw OM and ON perpendicular on AB and CD. Join OP, OB and OD. So OM and ON bisect AB and CD respectively. [Perpendicular drawn from the centre of a circle to a chord bisects it.] MB = ½ AB = ½ CD = ND ……. (i) In right triangle △ OMB, OM 2 = OB 2 – MB 2 ……. (ii) In right triangle △ OND, ON 2 = OD 2 – ND 2 ……. (iii) From equation (i), (ii) and (iii) OM = ON In △ OPM and △ OPN, ∠ OMP = ∠ ONP [both 90 0 ] OP = OP [Common] OM = ON [Proved] Using RHS criterion of congruence, △ OPM ≅ △ OPN PM = PN [c.p.c.t] By adding (i) both sides MB + PM = ND + PN BP = DP We know that AB = CD AB – BP = CD – DP [BP = DP] AP = CP Exercise 17C PAGE: 2201. In the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find:
(i) ∠ BOC
(ii) ∠ OBC
Solution:
From the given figure, △ ABC is an equilateral triangle. So all the three angles of the triangle will be 60 0 . ∠ A = ∠ B = ∠ C = 60 0 As the triangle is equilateral, BO and CO will be the angle of bisectors of ∠ B and ∠ C respectively. ∠ OBC = ∠ ABC/2 = 30 0 From the given figure, OB and OC are the radii of the given circle and are of equal length. △ OBC is isosceles triangle with OB = OC. In △ OBC, ∠ OBC = ∠ OCB as they are angles opposite to the two equal sides of an isosceles triangle. ∠ OBC = 30 0 and ∠ OCB = 30 0 As the sum of all the angles of a triangle is 180 0 In △ OBC, ∠ OCB + ∠ OBC + ∠ BOC = 180 0 Substituting the values 30 0 + 30 0 + ∠ BOC = 180 0 60 0 + ∠ BOC = 180 0 So we get ∠ BOC = 180 0 – 60 0 = 120 0 Therefore, ∠ BOC = 120 0 and ∠ OBC = 30 0 .2. In the given figure, a square is inscribed in a circle with centre O. Find:
(i) ∠ BOC
(ii) ∠ OCB
(iii) ∠ COD
(iv) ∠ BOD
Is BD a diameter of the circle?
Solution:
From the figure, extend a straight-line OB to BD and CO to CA. We get the diagonals of the square which intersect each other at 90 0 by the property of square. From the above mentioned statement, we know that ∠ COD = 90 0 Here the sum of the angle ∠ BOC and ∠ OCD is 180 0 as BD is a straight line. ∠ BOC + ∠ OCD = ∠ BOD = 180 0 It can be written as ∠ BOC + 90 0 = 180 0 ∠ BOC = 180 0 – 90 0 ∠ BOC = 90 0 Therefore, triangle OCB is an isosceles triangle with sides OB and OC of equal length as they are the radii of the same circle. In △ OCB, ∠ OBC = ∠ OCB [Opposite angles to the two equal sides of an isosceles triangle] Here sum of all the angles of a triangle is 180 0 ∠ OBC + ∠ OCB + ∠ BOC = 180 0 It can be written as ∠ OBC + ∠ OBC + 90 0 = 180 0 [∠ OBC = ∠ OCB] So we get 2 ∠ OBC = 180 0 – 90 0 2 ∠ OBC = 90 0 ∠ OBC = 45 0 Here, ∠ OBC = ∠ OCB = 45 0 Yes, BD is the diameter of the circle.3. In the given figure, AB is a side of regular pentagon and BC is a side of regular hexagon.
(i) ∠ AOB
(ii) ∠ BOC
(iii) ∠ AOC
(iv) ∠ OBA
(v) ∠ OBC
(vi) ∠ ABC
Solution:
Given – AB is the side of a pentagon where the angle subtended by each arm of the pentagon at the centre of the circle = 360 0 /5 = 72 0 Hence, ∠ AOB = 72 0 BC is the side of a hexagon where the angle subtended by BC at the centre = 360 0 /6 = 60 0 Hence, ∠ BOC = 60 0 ∠ AOC = ∠ AOB + ∠ BOC ∠ AOC = 72 0 + 60 0 = 132 0 The triangle formed i.e., △ AOB is an isosceles triangle with OA = OB as they are radii of the same circle. ∠ OBA = ∠ BAO [opposite angles of equal sides of an isosceles triangle] We know that the sum of all the angles of a triangle is 180 0 ∠ AOB + ∠ OBA + ∠ BAO = 180 0 2∠ OBA + 72 0 = 180 0 [∠ OBA = ∠ BAO] So we get 2 ∠ OBA = 180 0 – 72 0 2 ∠ OBA = 108 0 ∠ OBA = 54 0 Here ∠ OBA = ∠ BAO = 54 0 So the triangle formed, △ BOC is an isosceles triangle with OB = OC as they are radii of the same circle. ∠ OBC = ∠ OCB [opposite angles of equal sides of an isosceles triangle] We know that the sum of all the angles of a triangle is 180 0 ∠ BOC + ∠ OBC + ∠ OCB = 180 0 Substituting the values 2 ∠ OBC + 60 0 = 180 0 [∠ OBC = ∠ OCB] 2 ∠ OBC = 180 0 – 60 0 2 ∠ OBC = 120 0 ∠ OBC = 60 0 Here ∠ OBC = ∠ OCB = 60 0 So ∠ ABC = ∠ OBA + ∠ OBC = 54 0 + 60 0 = 114 04. In the given figure, arc AB and arc BC are equal in length. If ∠ AOB = 48 0 , find:
(i) ∠ BOC
(ii) ∠ OBC
(iii) ∠ AOC
(iv) ∠ OAC
Solution:
The arc of equal lengths subtends equal angles at the centre. ∠ AOB = ∠ BOC = 48 0 ∠ AOC = ∠ AOB + ∠ BOC = 48 0 + 48 0 = 96 0 So the triangle formed △ BOC is an isosceles triangle with OB = OC as they are radii of the same circle. ∠ OBC = ∠ OCB [opposite angles of equal sides of an isosceles triangle] We know that the sum of all the angles of a triangle is 180 0 ∠ BOC + ∠ OBC + ∠ OCB = 180 0 2 ∠ OBC + 48 0 = 180 0 [∠ OBC = ∠ OCB] 2 ∠ OBC = 180 0 – 48 0 2 ∠ OBC = 132 0 ∠ OBC = 66 0 Here ∠ OBC = ∠ OCB = 66 0 So the triangle formed △ AOC is an isosceles triangle with OA = OC as they are radii of the same circle ∠ OAC = ∠ OCA [opposite angles of equal sides of an isosceles triangle] We know that the sum of all the angles of a triangle is 180 0 ∠ COA + ∠ OAC + ∠ OCA = 180 0 Substituting the values 2 ∠ OAC + 96 0 = 180 0 [∠ OAC = ∠ OCA] 2 ∠ OAC = 180 0 – 96 0 2 ∠ OAC = 84 0 ∠ OAC = 42 0 Here ∠ OCA = ∠ OAC = 42 05. In the given figure, the lengths of arcs AB and BC are in the ratio 3:2. If ∠ AOB = 96 0 , find:
(i) ∠ BOC
(ii) ∠ ABC
Solution:
The two arcs are in the ratio 3:2 ∠ AOB : ∠ BOC = 3: 2 ∠ AOC = 96 0 So 3x = 96 x = 32 Hence, ∠ BOC = 2 × 32 = 64 0 So the triangle formed, △ AOB is an isosceles triangle with OA = OB as they are radii of the same circle. ∠ OBA = ∠ BAO [opposite angles of equal sides of an isosceles triangle] We know that the sum of all the angles of a triangle is 180 0 ∠ AOB + ∠ OBA + ∠ BAO = 180 0 2 ∠ OBA + 96 0 = 180 0 [∠ OBA = ∠ BAO] 2 ∠ OBA = 180 0 – 96 0 2 ∠ OBA = 84 0 2 ∠ OBA = 42 0 Here ∠ OBA = ∠ BAO = 42 0 So the triangle formed, △ BOC is an isosceles triangle with OB = OC as they are radii of the same circle. ∠ OBC = ∠ OCB [opposite angles of equal sides of an isosceles triangle] We know that the sum of all the angles of a triangle is 180 0 ∠ BOC + ∠ OBC + ∠ OCB = 180 0 2 ∠ OBC + 64 0 = 180 0 [∠ OBC = ∠ OCB] 2 ∠ OBC = 180 0 – 64 0 2 ∠ OBC = 116 0 ∠ OBC = 58 0 Here ∠ OBC = ∠ OCB = 58 0 ∠ ABC = ∠ BOA + ∠ OBC = 42 0 + 58 0 = 100 0ICSE Class 9 Maths Selina Solutions Chapter 17 Exercise 17D
1. The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centres.
Solution:
To find – OM Given – AB = 24 cm As OM ⊥ AB OM bisects AB AM = 12 cm In right △ OMA, OA 2 = OM 2 + AM 2 OM 2 = OA 2 – AM 2 Substituting the values OM 2 = 13 2 – 12 2 OM 2 = 25 OM = 5 cm Therefore, the distance of the chord from the centre is 5 cm.2. Prove that equal chords of congruent circles subtend equal angles at their centre.
Solution:
Given – AB and CD are two equal chords of congruent circles with centres O and O’ respectively. To prove – ∠ AOB = ∠ CO’D Proof – In △ OAB and △ O’CD OA = O’C (radii of congruent circles) OB = O’D (radii of congruent circles) AB = CD (Given) △ OAB ≅ △ O’CD [By SSS congruence criterion] ∠ AOB = ∠ CO’D [c.p.c.t]3. Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Solution:
The circle can have 0, 1 or 2 points in common. The maximum number of common points is 2.4. Suppose you are given a circle. Describe a method by which you can find the centre of this circle.
Solution:
In order to draw the centre of a given circle: 1. Construct the circle. 2. Taking any two different chords AB and CD of this circle, construct perpendicular bisectors of these chords. 3. Now let the perpendicular bisectors meet at point O. Hence, O is the centre of the given circle.5. Given two equal chords AB and CD of a circle, with centre O, intersecting each other at point P. Prove that:
(i) AP = CP
(ii) BP = DP
Solution:
In △ OMP and △ ONP, OP = OP (common side) ∠ OMP = ∠ ONP [Both are right angles] OM = OM [side both the chords are equal, so the distance of the chords from the centre are also equal] △ OMP ≅ △ ONP [RHS congruence criterion] MP = PN [cpct] …… (a) (i) AB = CD [given] AM = CN [Perpendicular drawn from the centre to the chord bisects the chord] AM + MP = CN + NP [from (a)] AP = CP …… (b) (ii) AB = CD AP + BP = CP + DP BP = DP [from (b)] Therefore, proved.Benefits of ICSE Class 9 Maths Selina Solutions Chapter 17
ICSE Class 9 Maths Selina Solutions for Chapter 17 on Circles provide numerous benefits to students. Here’s a comprehensive look at why these solutions is valuable: 1. Structured LearningClear Explanations: ICSE Class 9 Maths Selina Solutions Chapter 17 Circle offer step-by-step explanations to problems, which help students understand the process of solving circle-related problems.
Conceptual Clarity: The ICSE Class 9 Maths Selina Solutions Chapter 17 Circle are designed to clarify fundamental concepts, including the properties of circles, chords, tangents, and sectors.
2. Practice and MasteryDiverse Problems: By working through various problems in the ICSE Class 9 Maths Selina Solutions Chapter 17 Circle, students gain exposure to different types of questions and applications of circle properties.
Increased Proficiency: Regular practice using these ICSE Class 9 Maths Selina Solutions Chapter 17 Circle helps reinforce learning, making students more proficient in solving complex problems.
3. Exam PreparationAligned with ICSE Syllabus: Solutions are tailored to the ICSE curriculum, ensuring that students are well-prepared for their examinations.
Understanding Exam Patterns: By solving these problems, students familiarize themselves with the types of questions likely to appear in their exams, which aids in better preparation and time management.
4. Enhanced Problem-Solving SkillsAnalytical Skills: Working through the solutions develops students’ analytical and logical reasoning skills as they learn to apply circle properties and theorems to solve problems.
Critical Thinking: Students learn to approach problems from different angles and develop critical thinking skills that are beneficial for math and other subjects.
5. Self-Study and RevisionIndependent Learning: Solutions allow students to study and revise concepts on their own, providing a valuable resource for self-paced learning.
Error Correction: Students can check their answers and understand where they might have gone wrong, helping them correct mistakes and avoid repeating them.
Here at Physics Wallah we provide the Best CLASS 9 ONLINE COACHING to ease your exam preparation. Our class 9 online courses are taught by well-known instructors. We attempt to strengthen conceptual understanding and foster problem-solving abilities.ICSE Class 9 Maths Selina Solutions Chapter 17 FAQs
How to understand Circles chapter Class 9?
What is the full concept of a circle?
What is special about circles?
Who is known as the father of maths?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
