
ICSE Class 9 Maths Selina Solutions Chapter 16: ICSE Class 9 Maths Selina Solutions Chapter 16 Area Here are several theorems. It is crucial to comprehend the ideas covered in Class 9 since they are carried over into Class 10.
It is recommended that students complete the exercises in every chapter of the Selina book to achieve high scores on the mathematics exam for Class 9. These Selina maths solutions for class 9 aid students in better comprehending all of the material.ICSE Class 9 Maths Selina Solutions Chapter 16 Overview
ICSE Class 9 Maths Selina Solutions Chapter 16 on Area Theorems offers a concise and effective guide to understanding and applying important concepts in geometry. The ICSE Class 9 Maths Selina Solutions Chapter 16 covers essential theorems related to areas of triangles, quadrilaterals, and circles, presented with clear explanations and illustrative diagrams. With a focus on step-by-step solutions and practice problems, these solutions help students grasp geometric principles, enhance problem-solving skills, and prepare thoroughly for examinations. Overall, ICSE Class 9 Maths Selina Solutions Chapter 16 equips students with the knowledge and confidence to tackle area-related challenges in mathematics.ICSE Class 9 Maths Selina Solutions Chapter 16 PDF
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 16 in detail. This chapter will help you to clear all your doubts regarding the chapter Inequalities. Students are advised to prepare from these ICSE Class 9 Maths Selina Solutions Chapter 16 before the examinations to perform better.ICSE Class 9 Maths Selina Solutions Chapter 16 PDF
ICSE Class 9 Maths Selina Solutions Chapter 16 Area Theorems
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 16 -1. In the given figure, if the area of triangle ADE is 60 cm 2 , state, given reason, the area of:
(i) Parallelogram ABED
(ii) Rectangle ABCF
(iii) Triangle ABE
Solution:
(i) As ∆ADE and parallelogram ABED are on the same base AB and between the same parallels DE || AB, the area of the ∆ADE will be half the area of parallelogram ABED. So, Area of parallelogram ABED = 2 x Area of ∆ADE = 2 x 60 cm 2 = 120 cm 2 (ii) The area of a parallelogram is equal to the area of the rectangle on the same base and of the same altitude i.e., between the same parallels So, Area of rectangle ABCF = Area of parallelogram ABED = 120 cm 2 (iii) We know that the area of triangles on the same base and between the same parallel lines are equal So, Area of ∆ABE = Area of ∆ADE = 60 cm 22. The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB. Prove that:
(i) Quadrilateral CDEF is a parallelogram.
(ii) Area of quad. CDEF = Area of rect. ABDC + Area of || gm. ABEF.
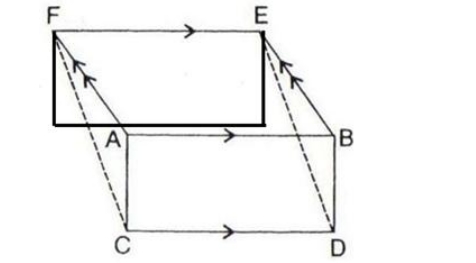
Solution:
After drawing the opposite sides of AB, we get it’s seen from the figure that CD|| FE. Therefore, FC must parallel to DE. Thus, it is proved that the quadrilateral CDEF is a parallelogram. We know that, The area of parallelograms on same base and between same parallel lines is always equal. Also, area of parallelogram is equal to the area of rectangle on the same base and of the same altitude i.e., between same parallel lines. So, Area of CDEF = Area of ABDC + Area of ABEF – Hence Proved.3. In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that:
(i) 2 Area (∆POS) = Area (||gm PMLS)
(ii) Area (∆POS) + Area (∆QOR) = ½ Area (||gm PQRS)
(iii) Area (∆POS) + Area (∆QOR) = Area (∆POQ) + Area (∆SOR).
Solution:
(i) As POS and parallelogram PMLS are on the same base PS and between the same parallels i.e., SP || LM Since O is the center of LM and ratio of areas of triangles with same vertex and bases along the same line is equal to ratio of their respective bases Also, the area of the parallelogram is twice the area of the triangle if they lie on the same base and in between the same parallels Thus, 2 Area (∆PSO) = Area(PMLS) (ii) Taking LHS, we have LM is parallel to PS and PS is parallel to RQ, therefore, LM is parallel to RQ And, since ∆ POS lie on the base PS and in between the parallels PS and LM, we have Area ( ∆ POS) = ½ Area (PSLM) Also, since ∆ QOR lie on the base QR and in between the parallels LM and RQ, we have Area ( ∆ QOR) = ½ Area (LMQR) Now, Area( ∆ POS) + Area( ∆ QOR) = ½ Area(PSLM) + ½ Area(LMQR) = ½ [Area(PSLM) + Area(LMQR)] = ½ Area(PQRS) (iii) We know that, the diagonals in a parallelogram bisect each other. So, OS = OQ In ∆ PQS, as OS = OQ OP is the median of the ∆ PQS. We know that median of a triangle divides it into two triangles of equal area. Therefore, Area ( ∆ POS) = Area ( ∆ POQ) … (1) Similarly, as OR is the median of the triangle QRS, we have Area ( ∆ QOR) = Area ( ∆ SOR) … (2) Now, adding (1) and (2) we get Area ( ∆ POS) + area ( ∆ QOR) = Area ( ∆ POQ) + Area ( ∆ SOR) – Hence Proved.4. In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ∆CPD and ∆AQD are equal in area.
(ii) Area (∆AQD) = Area (∆APD) + Area (∆CPB)
Solution:
Given, ABCD is a parallelogram. P and Q are any points on the sides AB and BC respectively. Join diagonals AC and BD. Proof: (i) As triangles with same base and between same set of parallel lines have equal areas Area ( ∆ CPD) = Area ( ∆ BCD) …… (1) Again, diagonals of the parallelogram bisect area in two equal parts Area ( ∆ BCD) = ½ area of parallelogram ABCD …… (2) From (1) and (2) Area ( ∆ CPD) = ½ Area (ABCD) …… (3) Similarly, Area ( ∆ AQD) = Area ( ∆ ABD) = ½ Area (ABCD) …… (4) From (3) and (4), we get Area ( ∆ CPD) = Area ( ∆ AQD) – Hence proved. (ii) We know that, area of triangles on the same base and between same parallel lines are equal So, Area of ∆ AQD = Area of ∆ ACD = Area of ∆ PDC = Area of ∆ BDC = Area of ∆ ABC = Area of ∆ APD + ∆ Area of BPC – Hence Proved5. In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is 48 cm 2
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
Solution:
(i) As ∆ BEC and parallelogram ABCD are on the same base BC and between the same parallels i.e., BC || AD. Area ( ∆ BEC) = ½ x Area (ABCD) = ½ x 48 = 24 cm 2 (ii) Area (ANMD) = Area (BNMC) = ½ x Area (ABCD) = ½ x 2 x Area ( ∆ BEC) = Area ( ∆ BEC) Therefore, the parallelograms ANMD and NBCM have areas equal to ∆ BEC.6. In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ∆ADE and quadrilateral ABCD are equal in area.
Solution:
As, ∆ DCB and ∆ DEB are on the same base DB and between the same parallels i.e., DB || CE, We have, Area ( ∆ DCB) = Area ( ∆ DEB) Area ( ∆ DCB + ∆ ADB) = Area ( ∆ DEB + ∆ ADB) Area (ABCD) = Area ( ∆ ADE) – Hence proved7. ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
Solution:
Its seen that, ∆ APB and parallelogram ABCD are on the same base AB and between the same parallel lines AB and CD. So, Ar( ∆ APB) = ½ Ar(||gm ABCD) … (i) Now,∆ ADQ and parallelogram ABCD are on the same base AD and between the same parallel lines AD and BQ.
So, Ar( ∆ ADQ) = ½ Ar(||gm ABCD) … (ii) On adding equation (i) and (ii), we get Ar( ∆ APB) + Ar(∆ ADQ) = ½ Ar(||gm ABCD) + ½ Ar(||gm ABCD) = Ar(||gm ABCD)
Ar(quad. ADQB) – Ar( ∆ BPQ) = Ar(||gm ABCD) Ar(quad. ADQB) – Ar( ∆ BPQ) = Ar(quad. ADQB) – Ar( ∆ DCQ) Ar( ∆ BPQ) = Ar( ∆ DCQ) Subtracting Ar( ∆ PCQ) from both the sides, we get Ar( ∆ BPQ) – Ar( ∆ PCQ) = Ar( ∆ DCQ) – Ar( ∆ PCQ) Ar( ∆ BCP) = Ar( ∆ DPQ) – Hence proved.8. The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
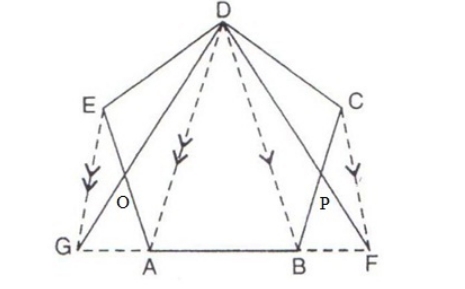
Solution:
It’s seen that triangles EDG and EGA are on the same base EG and between the same parallel lines EG and DA, so Ar( ∆ EDG) = Ar( ∆ EGA) On subtracting ∆ EOG from both sides, we have Ar( ∆ EDG) – Ar( ∆ EOG) = Ar( ∆ EGA) – Ar( ∆ EOG) Ar( ∆ EOD) = Ar( ∆ GOA) … (i) Similarly, Ar( ∆ DPC) = Ar( ∆ BPF) … (ii) Now, Ar(GDF) = Ar(GOA) + Ar(BPF) + Ar(pen. ABPDO) = Ar(EOD) + Ar(DPC) + Ar(pen. ABPDO) = Ar(pen. ABCDE) – Hence proved9. In the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the area of triangles ABC and BQP are equal.
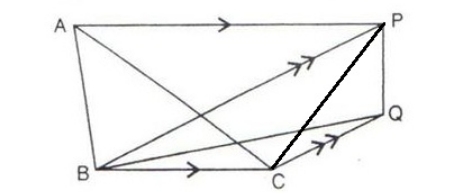
Solution:
On joining PC, we see that∆ ABC and ∆ BPC are on the same base BC and between the same parallel lines AP and BC.
Ar( ∆ ABC) = Ar( ∆ BPC) … (i) And, ∆ BPC and ∆ BQP are on the same base BP and between the same parallel lines BP and CQ. Ar( ∆ BPC) = Ar(BQP) … (ii) From (i) and (ii), we get Ar( ∆ ABC) = Ar( ∆ BQP) – Hence proved.10. In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH is perpendicular to FG prove that:
(i) ∆EAC ≅ ∆BAF.
(ii) Area of the square ABDE = Area of the rectangle ARHF.
Solution:
(i) From figure, ∠EAC = ∠EAB + ∠BAC = 90 o + ∠BAC … (i) ∠BAF = ∠FAC + ∠BAC = 90 o + ∠BAC … (ii) From (i) and (ii), we get ∠EAC = ∠BAF In ∆ EAC and ∆ BAF, we have, EA = AB ∠EAC = ∠BAF (proved above) AC = AF Therefore, ∆ EAC ≅ ∆ BAF (SAS axiom of congruency) (ii) As ∆ ABC is a right triangle, we have AC 2 = AB 2 + BC 2 [Using Pythagoras theorem in ∆ABC] AB 2 = AC 2 – BC 2 AB 2 = (AB 2 + BC 2 ) – [BR 2 + RC 2 ] [Since AC 2 = AR 2 + RC 2 and using Pythagoras Theorem in ∆BRC] AB 2 = AR 2 + 2AR × RC + RC 2 – (BR 2 + RC 2 ) [Using the identity] AB 2 = AR 2 + 2AR × RC + RC 2 – (AB 2 – AR 2 + RC 2 ) [Using Pythagoras Theorem in ∆ABR ] 2AB 2 = 2AR 2 + 2AR × RC AB 2 = AR (AR + RC) AB 2 = AR × AF ∴ Area (ABDE) = Area (rectangle ARHF)11. In the following figure, DE is parallel to BC. Show that:
(i) Area (∆ADC) = Area(∆AEB).
(ii) Area (∆BOD) = Area (∆COE).
Solution:
(i) In ∆ ABC, D is midpoint of AB and E is the midpoint of AC And, DE is parallel to BC So, by mid-point theorem, we have AD/AB = AE/AC Ar( ∆ ADC) = Ar( ∆ BDC) = ½ Ar( ∆ ABC) … (i) Again, Ar( ∆ AEB) = Ar( ∆ BEC) = ½ Ar( ∆ ABC) … (ii) From equations (i) and (ii), we have Area ( ∆ ADC) = Area( ∆ AEB). – Hence Proved (ii) We know that, area of triangles on the same base and between same parallel lines are equal So, Area( ∆ DBC) = Area( ∆ BCE) Area( ∆ DOB) + Area( ∆ BOC) = Area( ∆ BOC) + Area( ∆ COE) Thus, Area( ∆ DOB) = Area( ∆ COE) [On subtracting Area( ∆ BOC) on both sides]12. ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm 2 ; AB = 30 cm and BC = 40 cm; Calculate:
(i) Area of parallelogram ABCD
(ii) Area of the parallelogram BCFE
(iii) Length of altitude from A on CD
(iv) Area of triangle ECF
Solution:
(i) As ∆ EBC and parallelogram ABCD are on the same base BC and between the same parallels i.e., BC||AD. So, Area( ∆ EBC) = ½ Area(||gm ABCD) Area(||gm ABCD) = 2 x Ar( ∆ EBC) = 2 x 480 cm 2 = 960 cm 2 (ii) We know that, parallelograms on same base and between same parallels are equal in area So, Area of BCFE = Area of ABCD = 960 cm 2 (iii) Area of ∆ ACD = 960/2 = 480 = (1/2) x 30 x Altitude Thus, Altitude = 480/15 = 32 cm (iv) We know that, the area of a triangle is half that of a parallelogram on the same base and between the same parallels Therefore, Area( ∆ ECF) = ½ Area(||gm CBEF) Similarly, Area( ∆ BCE) = ½ Area(||gm CBEF) Thus, Area( ∆ ECF) = Area( ∆ BCE) = 960/2 = 480 cm 213. In the given figure, D is mid-point of side AB of ∆ABC and BDEC is a parallelogram.
Prove that: Area of ∆ABC = Area of ||gm BDEC.
Solution:
Here, AD = DB and EC = DB (Given) So, EC = AD It’s seen that EFC = AFD (Vertically opposite angles) And, as ED and CB are parallel lines with AC cutting these lines, we have ∠ECF = ∠FAD (Alternate interior angles) From the above conditions, we have∆ EFC ≅ ∆ AFD by AAS Congruency criterion
So, Area ( ∆ EFC) = Area ( ∆ AFD) Now, adding quadrilateral CBDF in both sides, we get Area of || gm BDEC = Area of ∆ ABC – Hence proved14. In the following, AC || PS || QR and PQ || DB || SR.
Prove that:
Area of quadrilateral PQRS = 2 × Area of quad. ABCD.
Solution:
In parallelogram PQRS, AC || PS || QR and PQ || DB || SR Similarly, AQRC and APSC are also parallelograms. As, ∆ ABC and parallelogram AQRC are on the same base AC and between the same parallels, we have Ar( ∆ ABC) = ½ Ar(AQRC)……(i) Similarly, Ar( ∆ ADC) = ½ Ar(APSC)…….(ii) On adding (i) and (ii), we get Ar( ∆ ABC) + Ar( ∆ ADC) = ½ Ar(AQRC) + ½ Ar(APSC) Area (quad. ABCD) = ½ Area (quad. PQRS) Therefore, Area of quad. PQRS = 2 × Area of quad. ABCD15. ABCD is trapezium with AB || DC. A line parallel to AC intersects AB at point M and BC at point N. Prove that: area of ΔADM = area of ΔACN.
Solution:
Given: ABCD is a trapezium AB || CD, MN || AC Let’s join C and M We know that, area of triangles on the same base and between same parallel lines are equal. So, Area of ΔAMD = Area of ΔAMC … (i) Similarly, considering quad. AMNC where MN || AC, we have ΔACM and ΔACN are on the same base and between the same parallel lines Thus, their areas should be equal. i.e., Area of ΔACM = Area of ΔCAN … (ii) From equations (i) and (ii), we get Area of ΔADM = Area of ΔCAN – Hence Proved.16. In the given figure, AD || BE || CF. Prove that area (ΔAEC) = area (ΔDBF)
Solution:
We know that, Area of triangles on the same base and between same parallel lines are equal. So, in ABED quadrilateral and AD||BE With common base, BE and between AD and BE parallel lines, we have Area of ΔABE = Area of ΔBDE … (i) Similarly, in BEFC quadrilateral and BE||CF With common base BC and between BE and CF parallel lines, we have Area of ΔBEC = Area of ΔBEF … (ii) On adding equations (i) and (ii), we get Area of ΔABE + Area of ΔBEC = Area of ΔBEF + Area of ΔBDE Thus, Area of ΔAEC = Area of ΔDBF – Hence Proved17. In the given figure, ABCD is a parallelogram; BC is produced to point X. Prove that: area (Δ ABX) = area (quad. ACXD).
Solution:
Given: ABCD is a parallelogram. We know that, Area of ΔABC = Area of ΔACD (Diagonal divides a ||gm into 2 triangles of equal area) Now, consider ΔABX Area of ΔABX = Area of ΔABC + Area of ΔACX We also know that, area of triangles on the same base and between same parallel lines are equal. So, Area of ΔACX = Area of ΔCXD From above equations, we have Area of ΔABX = Area of ΔABC + Area of ΔACX = Area of ΔACD+ Area of ΔCXD = Area of quadrilateral ACXD – Hence Proved18. The given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
Solution:
Let’s join B and R and also P and R. We know that, the area of the parallelogram is equal to twice the area of the triangle, if the triangle and the parallelogram are on the same base and between the parallels Taking ABCD parallelogram: As ||gm ABCD and ΔABR lie on AB and between the parallels AB and DC, we have Area (||gm ABCD) = 2 x Area (ΔABR) … (i) Also, the area of triangles with same base and between the same parallel lines are equal. As the triangles ABR and APR lie on the same base AR and between the parallels AR and QP, we have, Area (ΔABR) = Area (ΔAPR) … (ii) From equations (i) and (ii), we have Area (||gm ABCD) = 2 x Area (ΔAPR) … (iii) Also, its seen that APR and ||gm ARQP lie on the same base AR and between the same parallels AR and QP So, Area (ΔAPR) = ½ Area (||gm ARQP) … (iv) Using (iv) in (iii), we get Area (||gm ABCD) = 2 x ½ x Area (||gm ARQP) Area (||gm ABCD) = Area (||gm ARQP) – Hence provedExercise 16(B)
1. Show that:
(i) A diagonal divides a parallelogram into two triangles of equal area.
(ii) The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
(iii) The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
Solution:
(i) Let ABCD be a parallelogram (Given) Considering the triangles ABC and ADC, we have AB = CD (opposite sides of ||m) AD = BC (opposite sides of ||gm) AD = AD (Common) Thus, ΔABC ≅ ΔADC by SSS congruence criterion Area of congruent triangles are equal. Therefore, Area (ΔABC) = Area (ΔADC) (ii) Consider the following figure: Here AP ⊥ BC, We have, Ar.(ΔABD) = ½ BD x AP And, Ar.(ΔADC) = ½ DC x AP Thus, Area(ΔABD)/Area(ΔADC) = (½ × BD × AP)/ (½ × DC × AP) = BD/DC – Hence proved (iii) Consider the following figure: Here, Ar.(ΔABC) = ½ BM x AC And, Ar.(ΔADC) = ½ DN x AC Thus, Area(ΔABC)/Area(ΔADC) = (½ × BM × AC)/ (½ × DN × AC) = BM/DN – Hence proved2. In the given figure; AD is median of Δ ABC and E is any point on median AD. Prove that Area ( Δ ABE) = Area ( Δ ACE).
Solution:
As AD is the median of ΔABC, it will divide ΔABC into two triangles of equal areas. So, Area (ΔABD) = Area (ΔACD) … (i) Also, since ED is the median of ΔEBC So, Area (ΔEBD) = Area (ΔECD) … (ii) On subtracting equation (ii) from (i), we have Area (ΔABD) – Area(ΔEBD) = Area(ΔACD) – Area(ΔECD) Therefore, Area (ΔABE) = Area (ΔACE) – Hence proved3. In the figure of question 2, if E is the midpoint of median AD, then prove that:
Area ( Δ ABE) = ¼ Area ( Δ ABC).
Solution:
As AD is the median of ΔABC, it will divide ΔABC into two triangles of equal areas. Hence, Area (ΔABD) = Area (ΔACD) Area (ΔABD) = ½ Area (ΔABC) … (i) In ΔABD, E is the mid-point of AD. So, BE is the median. Thus, Area (ΔBED) = Area (ΔABE) Area (ΔBED) = ½ Area (ΔABD) Area (ΔBED) = ½ x ½ Area (ΔABC) … [From equation (i)] Therefore, Area (ΔBED) = ¼ Area (ΔABC)4. ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = 1/8 of the area of parallelogram ABCD.
Solution:
Let’s join PD and BD. BD is the diagonal of the parallelogram ABCD. Thus, it divides the parallelogram into two equal parts of area. So, Area (ΔABD) = Area (ΔDBC) = ½ Area (parallelogram ABCD) … (i) Now, DP is the median of ΔABD. Thus, it will divide ΔABD into two triangles of equal areas. So, Area(ΔAPD) = Area (ΔDPB) = ½ Area (ΔABD) = ½ x (½ x Area (parallelogram ABCD)) [from equation (i)] = ¼ Area (parallelogram ABCD) … (ii) Similarly, In ΔAPD, Q is the mid-point of AD. Hence, PQ is the median. So, Area (ΔAPQ) = Area(ΔDPQ) = ½ Area (ΔAPD) = ½ x (¼ Area (parallelogram ABCD)) [Using equation (ii)] Therefore, Area (ΔAPQ) = 1/8 Area (parallelogram ABCD) – Hence proved.Benefits of ICSE Class 9 Maths Selina Solutions Chapter 16
Studying from Selina Solutions for ICSE Class 9 Maths Chapter 16 on Area Theorems offers several benefits:Clear Explanation : ICSE Class 9 Maths Selina Solutions Chapter 16 provide clear explanations of each area theorem, making it easier for students to understand the concepts and their applications.
Step-by-step Approach : The ICSE Class 9 Maths Selina Solutions Chapter 16 break down complex theorems into manageable steps, helping students follow the logical progression of proofs and derivations.
Illustrative Diagrams : Each theorem is accompanied by diagrams that visually represent geometric shapes and measurements, enhancing comprehension and visualization skills.
Practice Problems : The ICSE Class 9 Maths Selina Solutions Chapter 16 include a variety of practice problems that reinforce understanding and mastery of area theorems. These problems cover different scenarios and levels of difficulty, preparing students for exams and real-world applications.
Exam Preparation : By studying from Selina Solutions, students can effectively prepare for exams by focusing on key concepts, important formulas, and solving typical exam-style questions.
ICSE Class 9 Maths Selina Solutions Chapter 16 FAQs
What is the concise area theorem Class 9?
What is the area theorem class 9?
What is the theorem of Chapter 13 Class 9?
What is the mid point theorem class 9 proof?










