ICSE Class 9 Maths Selina Solutions Chapter 14 Rectilinear Figures
Neha Tanna11 Jul, 2024
Share
ICSE Class 9 Maths Selina Solutions Chapter 14: ICSE Class 9 Maths Selina Solutions Chapter 14 is thought to be very helpful for ICSE Class 9 Maths exam preparation. We provide you with thorough ICSE Class 9 Maths Selina Solutions Chapter 14 Rectilinear Figures exercises here.
Several quadrilaterals, including the parallelogram, rectangle, rhombus, square, and trapezium, are covered in this chapter. This page contains the ICSE Class 9 Maths Selina Solutions Chapter 14 in PDF format, which can be viewed online or downloaded.ICSE Class 9 Maths Selina Solutions Chapter 14 Overview
ICSE Class 9 Maths Selina Solutions Chapter 14 focuses on Rectilinear Figures and is covered comprehensively in Selina Solutions. These solutions provide clear explanations and step-by-step guidance for all exercises, helping students grasp concepts effectively. They include examples that illustrate various problem-solving techniques, aiding in better understanding and application. By using Selina Solutions, students can strengthen their problem-solving skills, revise effectively, and prepare confidently for exams, ensuring thorough comprehension and readiness in Rectilinear Figures.ICSE Class 9 Maths Selina Solutions Chapter 14 PDF
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 14 in detail. This chapter will help you to clear all your doubts regarding the chapter Inequalities. Students are advised to prepare from these ICSE Class 9 Maths Selina Solutions Chapter 14 before the examinations to perform better.ICSE Class 9 Maths Selina Solutions Chapter 14 PDF
ICSE Class 9 Maths Selina Solutions Chapter 14 Rectilinear Figures
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 14 -1. The sum of the interior angles of a polygon is four times the sum of its exterior angles. Find the number of sides in the polygon.
Solution:
The sum of the interior angle=4 times the sum of the exterior angles. Therefore, the sum of the interior angles = 4×360° =1440°. Now we have (2n – 4) × 90 o = 1440 o 2n – 4 = 16 2n = 16 + 4 2n = 20 n = 20/2 n = 10 Thus, the number of sides in the polygon is 10.2. The angles of a pentagon are in the ratio 4: 8: 6 : 4: 5. Find each angle of the pentagon.
Solution:
Let the angles of the pentagon are 4x, 8x, 6x, 4x and 5x. Thus, we can write 4x + 8x + 6x + 4x + 5x = 540 o 27x = 540 o x = 20 o Hence the angles of the pentagon are: 4×20 o = 80 o , 8×20 o = 160 o , 6×20 o = 120 o , 4×20 o = 80 o , 5×20 o = 100 o3. One angle of a six-sided polygon is 140 o and the other angles are equal. Find the measure of each equal angle.
Solution:
Let the measure of each equal angle be x. Then we can write 140 o + 5x = (2 × 6 – 4) × 90 o 140 o + 5x = 720 o 5x = 580 o x = 116 o Therefore, the measure of each equal angle are 116 o4. In a polygon there are 5 right angles and the remaining angles are equal to 195 o each. Find the number of sides in the polygon.
Solution:
Let the number of sides of the polygon be n and there are k angles with measure 195 o . Therefore, we can write: 5 × 90 o + k × 195 o = (2n – 4) 90 o 180 o n – 195 o k = 450 o – 360 o 180 o n – 195 o k = 90 o 12n – 13k = 90 o In this linear equation, n and k must be integer. Therefore, to satisfy this equation the minimum value of k must be 6 to get n as an integer. Hence the number of sides are 5 + 6 = 11.5. Three angles of a seven-sided polygon are 132 o each and the remaining four angles are equal. Find the value of each equal angle.
Solution:
Let the measure of each equal angle are x. Then we can write 3 × 132 o + 4x = (2 × 7 – 4) 90 o 4x = 900 o – 396 o 4x = 504 o x = 126 o Thus, the measure of each equal angle is 126 o .6. Two angles of an eight-sided polygon are 142 o and 176 o . If the remaining angles are equal to each other; find the magnitude of each of the equal angles.
Solution:
Let the measure of each equal side of the polygon be x. Then we can write: 142 o + 176 o + 6x = (2 × 8 – 4) 90 o 6x = 1080 o – 318 o 6x = 762 o x = 127 o Thus, the measure of each equal angle is 127 o7. In a pentagon ABCDE, AB is parallel to DC and ∠A: ∠E : ∠D = 3: 4 : 5. Find angle E.
Solution:
Let the measure of the angles are 3x, 4x and 5x. Thus ∠A + ∠B + ∠C + ∠D + ∠E = 540 o 3x + (∠B + ∠C) + 4x + 5x = 540 o 12x + 180 o = 540 o 12x = 360 o x = 30 o Thus, the measure of angle E will be 4 × 30 o = 120 o8. AB, BC, and CD are the three consecutive sides of a regular polygon. If ∠BAC = 15 o ; find,
(i) Each interior angle of the polygon.
(ii) Each exterior angle of the polygon.
(iii) Number of sides of the polygon.
Solution:
(i) Let each angle measure x degree. Therefore, a measure of each angle will be: x – 180 o – 2 × 15 o = 150 o (ii) Let each angle measure x degree. Therefore, a measure of each exterior angle will be: x = 180 o – 150 o = 30 o (iii) Let the number of each sides is n. Now we can write n . 150 o = (2n – 4) × 90 o 180 o n – 150 o n = 360 o 30 0 n = 360 o n = 12 Thus, the number of sides are 12.9. The ratio between an exterior angle and an interior angle of a regular polygon is 2 : 3. Find the number of sides in the polygon.
Solution:
Let measure of each interior and exterior angles are 3k and 2k. Let number of sides of the polygon is n. Now we can write: n. 3k = (2n – 4) × 90 o 3nk = (2n – 4) 90 o ……… (1) Again n. 2k = 360 o nk = 180 o from (1) 3. 180 o = (2n – 4)90 o 3 = n – 2 n = 5 Thus, the number of sides of the polygon is 5.10. The difference between an exterior angle of (n – 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6 o find the value of n.
Solution:
For (n-1) sided regular polygon: Let measure of each angle is x. Therefore (n – 1) x = (2 (n -1) – 4) 90 o x = (n-3/ n – 1) 180 o For (n+1) sided regular polygon: Let measure of each angle is y. Therefore (n + 2) y = (2 (n + 2) – 4) 90 o y = (n/ n + 2) 180 o now we have y – x = 6 o (n/ n + 2) 180 o – (n-3/ n – 1) 180 o = 6 o (n /n + 2) – (n – 3/ n – 1) = 1/30 30 n(n – 1) – 30 (n – 3) (n + 2) = (n + 2) (n -1) n 2 + n – 182 = 0 (n – 13) (n + 14) = 0 n = 13, -14 Thus, the value of n is 13. Exercise 14B PAGE: 1751. State, ‘true’ or ‘false’
(i) The diagonals of a rectangle bisect each other.
(ii) The diagonals of a quadrilateral bisect each other.
(iii) The diagonals of a parallelogram bisect each other at right angle.
(iv) Each diagonal of a rhombus bisects it.
(v) The quadrilateral, whose four sides are equal, is a square.
(vi) Every rhombus is a parallelogram.
(vii) Every parallelogram is a rhombus.
(viii) Diagonals of a rhombus are equal.
(ix) If two adjacent sides of a parallelogram are equal, it is a rhombus.
(x) If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
Solution:
(i)True. This is true, because we know that a rectangle is a parallelogram. So, all the properties of a parallelogram are true for a rectangle. Since the diagonals of a parallelogram bisect each other, the same holds true for a rectangle. (ii)False This is not true for any random quadrilateral. Observe the quadrilateral shown below.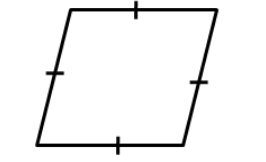
Clearly the diagonals of the given quadrilateral do not bisect each other. However, if the quadrilateral was a special quadrilateral like a parallelogram, this would hold true.
(iii)False
Consider a rectangle as shown below.
It is a parallelogram. However, the diagonals of a rectangle do not intersect at right angles, even though they bisect each other.
(iv)True
Since a rhombus is a parallelogram, and we know that the diagonals of a parallelogram bisect each other, hence the diagonals of a rhombus too, bisect other.
(v)False
This need not be true, since if the angles of the quadrilateral are not right angles, the quadrilateral would be a rhombus rather than a square.
(vi)True
A parallelogram is a quadrilateral with opposite sides parallel and equal.
Since opposite sides of a rhombus are parallel, and all the sides of the rhombus are equal, a rhombus is a parallelogram.
(vii)False
This is false, since a parallelogram in general does not have all its sides equal. Only opposite sides of a parallelogram are equal. However, a rhombus has all its sides equal. So, every parallelogram cannot be a rhombus, except those parallelograms that have all equal sides.
(viii)False
This is a property of a rhombus. The diagonals of a rhombus need not be equal.
(ix)True
A parallelogram is a quadrilateral with opposite sides parallel and equal.
A rhombus is a quadrilateral with opposite sides parallel, and all sides equal.
If in a parallelogram the adjacent sides are equal, it means all the sides of the parallelogram are equal, thus forming a rhombus.
(x)False
2. In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90 o.
Solution:
From the given figure we can conclude that ∠A + ∠D = 180 o [since consecutive angles are supplementary] ∠A/2 + ∠D/2 = 90 Again, from triangle ADM ∠A/2 + ∠D/2 + ∠M = 180 o 90 o + ∠M = 180 o ∠M = 180 o = 90 o Hence ∠AMD = 90 o3. In the following figure, AE and BC are equal and parallel and the three sides AB, CD and DE are equal to one another. If angle A is 102 o . Find angles AEC and BCD.
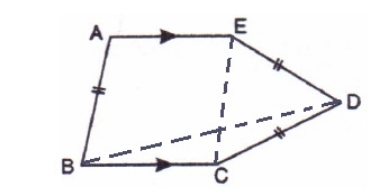
Solution:
According to the question, Given that AE = BC We have to find ∠AEC and ∠BCD Let us join EC and BD In the quadrilateral AECB AE = BC and AB = EC Also, AE parallel to BC So quadrilateral is a parallelogram. In parallelogram consecutive angles are supplementary ∠A + ∠B = 180 o 102 o + ∠B = 180 o ∠B = 78 o In parallelogram opposite angles are equal ∠A = ∠BEC and ∠B = ∠AEC ∠BEC = 102 o and ∠AEC = 78 o Now consider triangle ECD EC = ED = CD [since AB = EC] Therefore, triangle ECD is an equilateral triangle. ∠ECD = 60 o ∠BCD = ∠BEC + ∠ECD ∠BCD = 102 o + 60 o ∠BCD = 162 o Therefore, ∠AEC = 78 o and ∠BCD = 162 o4. In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
(i) ∠POC = 22 ½ o
(ii) ∠BDC = 2 ∠POC
(iii) ∠BOP = 3 ∠CPO
Solution:
Given ABCD is a square and diagonal meet at o. P is a point on BC such that OB = BP In the triangle BOC and triangle DOC BD = BD [common side] BO = CO OD = OC [since diagonals cuts at O] △ BOC ≅ △ DOC [By SSS postulate] Therefore, ∠BOC = 90 o Now ∠ POC = 22.5∠ BOP = 67.5
Again, in triangle BDC∠ BDC = 45 o [since ∠ B = 45 o and ∠ C = 90 o ]
Therefore∠ BDC = 2 ∠ POC
∠ BOP = 67.5 o
∠ BOP = 2 ∠ POC
Hence the proof.5. The given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
(i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
Solution:
In the given figure, triangle APB is an equilateral triangle Therefore, all its angles are 60 o Again, in the triangle ADB∠ ABD = 45 o
∠ AOB = 180 o – 60 o – 45 o
= 75 o Again, in triangle BPC∠ BPC = 75 o [since BP = CB]
Now,∠ C = ∠ BCP + ∠ PCD
∠ PCD = 90 o – 75 o
∠ PCD = 15 o
Therefore∠ APC = 60 o + 75 o
∠ APC = 135 o
Reflex ∠ APD = 360 o – 135 o = 225 o Therefore (i) ∠ AOB = 75 o (ii) ∠ BPC = 75 o (iii) ∠ PCD = 15 o (iv) Reflex ∠ APC = 225 o Exercise 14c PAGE: 1811. E is the mid-point of side AB and F is the midpoint of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
Solution:
Let us draw a parallelogram ABCD Where F is the midpoint Of side DC of parallelogram ABCD To prove: AEFD is a parallelogram Proof: In quadrilateral ABCD AB parallel to DC BC parallel to AD AB = DC Multiply both side by ½ ½ AB = ½ DC AE = DF Also, AD parallel to EF Therefore, AEFC is a parallelogram.2. The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
Solution:
Given ABCD is a parallelogram where the diagonal BD bisects parallelogram ABCD at angle B and D To prove: ABCD is a rhombus Proof: Let us draw a parallelogram ABCD where the diagonal BD bisects the parallelogram at angle B and D. Construction: Let us join AC as a diagonal of the parallelogram ABCD Since ABCD is a parallelogram Therefore, AB = DC AD = BC Diagonal BD bisects angle B and D So ∠COD = ∠DOA Again, AC also bisects at A and C Therefore ∠AOB = ∠BOC Thus, ABCD is a rhombus. Hence proved3. The alongside figure shows a parallelogram ABCD in which AE = EF = FC. Prove that:
(i) DE is parallel to FB
(ii) DE = FB
(iii) DEBF is a parallelogram.
Solution:
Construction: Join DF and EB Join diagonal BD Since the diagonals of a parallelogram bisect each other Therefore, OA = OC and OB = OD Also, AE = EF = FC Now, OA = OC and AE = FC OA – OC = OC – FC OE = OF Thus, in quadrilateral DEFB, we have OB = OD and OE = OF Diagonals of a quadrilateral DEFB bisect each other. DEFB is a parallelogram DE is parallel to FB DE = FB (opposite sides are equal)4. In the alongside diagram, ABCD is a parallelogram in which AP bisects angle AP bisects angle A and BQ bisects angle B. Prove that:
(i) AQ = BP
(ii) PQ = CD.
(iii) ABPQ is a parallelogram.
Solution:
Consider the triangle AOQ and triangle BOP ∠AOQ = ∠BOP [opposite angles] ∠OAQ = ∠BPO [alternate angles] △ AOQ ≅ △ BOP Hence AQ = BP Consider the triangle QOP and triangle AOB ∠AOB = ∠QOP [opposite angles] ∠OAB = ∠APQ [alternate angles] △ QOP ≅ △ AOB Hence PQ = AB = CD Consider the quadrilateral QPCD DQ = CP and DQ parallel to CP Also, QP = DC and AB parallel to QP parallel to DC Hence quadrilateral QPCD is a parallelogram.5. In the given figure, ABCD is a parallelogram. Prove that: AB = 2 BC.
Solution:
Given: ABCD is a parallelogram To prove: AB = 2BC Proof: ABCD is a parallelogram ∠A + ∠D = ∠B + ∠C = 180 o From the triangle AEB we have ∠A/2 + ∠B/2 + ∠E = 180 o ∠A – ∠A/2 + ∠D + ∠E 1 = 180 o [taking E 1 as a new angle] ∠A + ∠D + ∠E 1 = 180 o + ∠A/2 ∠E 1 = ∠A/2 [since ∠A + ∠D = 180 o ] Again, similarly ∠E 2 = ∠B/2 Now, AB = DE + EC = AD + BC = 2 BC [since AD = BC]Benefits of ICSE Class 9 Maths Selina Solutions Chapter 14
ICSE Class 9 Maths Selina Solutions Chapter 14 on Rectilinear Figures, offer several benefits to students:Comprehensive Coverage : The solutions provided in Selina for ICSE Class 9 Maths are comprehensive and cover all the topics and exercises in Chapter 14 of Rectilinear Figures. This ensures that students have access to detailed explanations for every problem they encounter.
Clarity of Concepts : The ICSE Class 9 Maths Selina Solutions Chapter 14 are designed to clarify the underlying concepts of Rectilinear Figures. They provide step-by-step explanations, making it easier for students to understand the principles involved in solving problems related to this chapter.
Practice and Revision : By using ICSE Class 9 Maths Selina Solutions Chapter 14, students can effectively practice and revise the material covered in class. Each exercise is accompanied by solutions that not only provide answers but also guide students through the logical steps needed to arrive at those answers.
Examples for Better Understanding : The solutions often include worked examples that illustrate different types of problems and their solutions. These examples serve as models for students to follow when tackling similar problems on their own.
Exam Preparation : Selina Solutions are valuable tools for exam preparation. They help students become familiar with the types of questions that may appear on exams and provide them with the confidence to tackle these questions effectively.
ICSE Class 9 Maths Selina Solutions Chapter 14 FAQs
What are rectilinear figures class 9 ICSE?
What are the rectilinear figures of a quadrilateral?
What are the properties of a rectilinear figure?
Why are rectilinear figures important?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
