ICSE Class 9 Maths Selina Solutions Chapter 12 Mid Point and Its Converse
Neha Tanna11 Jul, 2024
Share
ICSE Class 9 Maths Selina Solutions Chapter 12: Here are the Selina Solutions for the problems found in the ICSE Class 9 Maths Selina Solutions Chapter 12, Mid-Point and Its Converse. Students study the intercept theorem in detail as well as the issue of mid-point and its converse of a triangle in this chapter. By completing all of the questions in the Selina textbook, students can easily receive a perfect score on their exams.
The ICSE Class 9 Maths Selina Solutions Chapter 12 is quite simple to comprehend. All the exercise questions in the book are addressed in these solutions, which follow the ICSE or CISCE syllabus. This page contains the ICSE Class 9 Maths Selina Solutions Chapter 12 PDF, which can be viewed online or downloaded. To practice offline, students can now access and download the Selina Solutions for free.ICSE Class 9 Maths Selina Solutions Chapter 12 Overview
ICSE Class 9 Maths Selina Solutions Chapter 12, "Mid Point and Its Converse," offer clear explanations and step-by-step solutions to understand the concept of midpoints in geometry. This chapter focuses on properties and theorems related to midpoints of line segments. It covers topics such as the midpoint formula, properties of line segments divided by their midpoint, and the converse theorems associated with these properties. The solutions provided are structured to help students grasp the concepts effectively, with plenty of practice exercises to reinforce learning. Overall, ICSE Class 9 Maths Selina Solutions Chapter 12 for this chapter serves as a valuable resource for students aiming to strengthen their understanding and problem-solving skills in geometry.ICSE Class 9 Maths Selina Solutions Chapter 12 PDF
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 12 in detail. This chapter will help you to clear all your doubts regarding the chapter Inequalities. Students are advised to prepare from these ICSE Class 9 Maths Selina Solutions Chapter 12 before the examinations to perform better.ICSE Class 9 Maths Selina Solutions Chapter 12 PDF
ICSE Class 9 Maths Selina Solutions Chapter 12 Exercise
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 12 -1. In triangle ABC, M is the mid-point of AB, and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if BC = 7 cm and AC = 5 cm.
Solution:
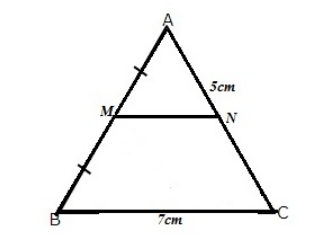The triangle is shown below:
Since M is the midpoint of AB and MN || BC
Then, by the mid-point theorem N is the midpoint of AC.
Therefore,
MN = ½ BC = ½ × 7 = 3.5cm
And, AN = ½ AC = ½ × 5 = 2.5cm
2. Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
Solution:
The figure is shown below: Let ABCD be a rectangle, with P, Q, R, and S representing the AB, BC, CD, and DA midpoints. The next step is to demonstrate that PQRS is a rhombus.
The two diagonals BD and AC should be drawn as seen in the figure
And, BD = AC [Since diagonals of a rectangle are equal]
Proof:
From ∆ABD and ∆BCD, we have
PS = ½ BD = QR and PS || BD || QR
2PS = 2QR = BD and PS || QR … (1)
Similarly,
2PQ = 2SR = AC and PQ || SR … (2)
From (1) and (2) we get
PQ = QR = RS = PS
Therefore, PQRS is a rhombus.
– Hence proved
3. D, E, and F are the mid-points of the sides AB, BC, and CA of an isosceles ∆ ABC in which AB = BC. Prove that ∆ DEF is also isosceles.
Solution:
The figure is shown below: Given that AB = AC and that ABC is an isosceles triangle Since the midpoints of AB, BC, and CA are, respectively, D, E, and F Therefore, by the mid-point theorem 2DE = AC and 2EF = AB ⇒ DE = EF Therefore, DEF is an isosceles triangle where DE = EF. – Hence proved4. The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
PR = ½ (AB + CD)
Solution:
Given, P is the midway between AD and PR || AB in ∆ABD. Q is therefore BD's midpoint. Using the midpoint theorem Similarly, R is the midpoint of BC as PR || CD || AB Now, from ∆ABD 2PQ = AB … (1) And, from ∆BCD 2QR = CD … (2) Adding (1) and (2), we get 2(PQ + QR) = AB + CD 2PR = AB + CD PR = ½ (AB + CD) – Hence proved.5. The figure, given below, shows a trapezium ABCD. M and N are the mid-points of the non-parallel sides AD and BC respectively. Find:
(i) MN, if AB = 11 cm and DC = 8 cm.
(ii) AB, if DC = 20 cm and MN = 27 cm.
(iii) DC, if MN = 15 cm and AB = 23 cm.
Solution:
Let’s draw a diagonal AC as shown in the figure below, (i) Given, AB = 11cm and CD = 8cm From ∆ABC, we have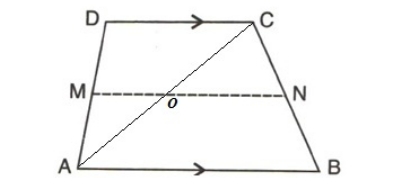
ON = ½ AB = ½ × 11 = 5.5cm
From ∆ACD, we have
OM = ½ CD = ½ × 8 = 4cm
Hence, MN = OM +ON
= (4 + 5.5)
= 9.5cm
(ii) Given, CD = 20cm and MN = 27cm
From ∆ACD, we have
OM = ½ CD = ½ × 20 = 10cm
Therefore, ON = 27 – 10 = 17cm
Then from ∆ABC, we have
AB = 2 ON
= 2 × 17
= 34cm
(iii) Given, AB = 23cm and MN = 15cm
From ∆ABC, we have
ON = ½ AB = ½ × 23 = 11.5cm
Therefore, OM = 15 – 11.5 = 3.5cm
Then from ∆ACD, we have
CD = 2 OM
= 2 × 3.5
= 7cm
6. The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
Solution:
The figure is shown below: Let ABCD be a quadrilateral, with P, Q, R, and S representing the AB, BC, CD, and DA midpoints. At point O, the diagonals AC and BD connect at a straight angle. Proof that PQRS is a rectangle is necessary. Proof: From ∆ABC and ∆ADC, we have 2PQ = AC and PQ || AC … (1) 2RS = AC and RS || AC … (2) From (1) and (2) we get, PQ = RS and PQ || RS Similarly, PS = RQ and PS||RQ Therefore, PQRS is a parallelogram. Now as PQ||AC, we have ∠AOD = ∠PXO = 90 o [Corresponding angles] Again, as BD||RQ, we have ∠PXO = ∠RQX = 90 o [Corresponding angle] Similarly, ∠QRS = ∠RSP = ∠SPQ = 90 o Therefore, PQRS is a rectangle. – Hence proved7. L and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
Solution:
The required figure is shown below: We have, BL = DM and BL || DM and BLMD is a parallelogram ⇒ BM || DL Now, in ∆ABY, we have L is the midpoint of AB and XL || BY, Therefore, x is the midpoint of AY ⇒ AX = XY … (1) Similarly for triangle CDX ⇒ CY = XY … (2) From (1) and (2), we get AX = XY = CY and AC = AX + XY + CY Consequently, the parallelogram ABCD's diagonal AC is trisected by segments DL and BM.8. ABCD is a quadrilateral in which AD = BC. E, F, G, and H are the mid-points of AB, BD, CD, and Ac respectively. Prove that EFGH is a rhombus.
Solution:
Given, AD = BC … (1) From the figure, In ∆ADC and ∆ABD, we have 2GH = AD and 2EF = AD, ⇒ 2GH = 2EF = AD … (2) Now, in ∆BCD and ∆ABC, we have 2GF = BC and 2EH = BC ⇒ 2GF = 2EH = BC … (3) From (1), (2), (3) we get 2GH = 2EF = 2GF = 2EH ⇒ GH = EF = GF = EH Therefore, EFGH is a rhombus. – Hence proved9. A parallelogram ABCD has P as the mid-point of DC and Q as a point of AC such that CQ = ¼ AC. PQ produced meets BC at R.
Prove that:
(i) R is the midpoint of BC
(ii) PR = ½ DB
Solution:
Let’s draw the diagonal BD as shown below. At point X, the diagonal cuts AC and BD meet. A parallelogram's diagonals are known to bisect one another. Therefore, AX = CX and BX = DX Given, CQ = ¼ AC CQ = ¼ × 2CX CQ = ½ CX Therefore, Q is the midpoint of CX. (i) For ∆CDX, PQ || DX or PR || BD And in ∆CBX, Q is the midpoint of CX and QR||BX Therefore, R is the midpoint of BC (ii) In ∆BCD, As P and R are the midpoint of CD and B, we have Thus, PR = ½ DB10. D, E, and F are the mid-points of the sides AB, BC, and CA respectively of ∆ ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
Solution:
The required figure is shown below: In ∆ABC and ∆OBC, we have 2DE = BC and 2PQ = BC, Therefore, DE = PQ … (1) In ∆ABO and ∆ACO, we have 2PD = AO and 2FQ = AO, Therefore, PD = FQ … (2) From (1) and (2), we get that PQFD is a parallelogram. – Hence proved.11. In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that:
(i) AP = 2AR
(ii) BC = 4QR
Solution:
The required figure is shown below: P is the midpoint of BC, PQ || AC, and QR || BC, as can be seen. Consequently, Q and R are the midpoints of AB and AP, respectively. (i) Thus, AP = 2AR (ii) Let’s extend QR such that it cuts AC at S as shown in the figure. Now, in ∆PQR and ∆ARS, we have ∠PQR = ∠ARS (Opposite angles) PR = AR PQ = AS (Since, PQ = AS = ½ AC) Thus, ∆PQR ≅ ∆ARS by SAS congruence criterion Therefore, by CPCT QR = RS Now, BC = 2QS BC = 2 × 2QR BC = 4QR – Hence proved12. In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that:
(i) Point P bisects BE,
(ii) PQ is parallel to AB.
Solution:
The required figure is shown below: (i) In ∆PED and ∆ABP, we have PD = AP [Since P is the mid-point of AD] ∠DPE = ∠APB [Opposite angles] ∠PED = ∠PBA [Alternate angles as AB || CE] ∴ ∆PED ≅ ∆ABP by ASA congruence postulate Thus, by CPCT EP = BP (ii) For ∆ECB, we have PQ||CE Also, CE||AB Therefore, PQ||AB – Hence proved13. In a triangle ABC, AD is a median and E is the mid-point of median AD. A line through B and E meets AC at point F. Prove that AC = 3AF.
Solution:
The required figure is shown below: Let’s draw a line DG || BF Now, In ∆ADG, we have DG || BF and E is the midpoint of AD Therefore, F is the midpoint of AG ⇒ AF = GF … (1) And, in ∆BCF, we have DG || BF and D is the midpoint of BC Therefore, G is the midpoint of CF ⇒ GF=CF … (2) AC = AF + GF + CF [From figure] AC = 3AF [From (1) and (2)] – Hence proved.14. D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
(i) Prove that BDFE is parallelogram
(ii) Find AB, if EF = 4.8 cm.
Solution:
The required figure is shown below: (i) Since F is the midpoint and EF || AB Therefore, E is the midpoint of BC So, BE = ½ BC and EF = ½ AB … (1) And, Since D and F are the midpoint of AB and AC Therefore, DE||BC So, DF = ½ BC and DB = ½ AB … (2) From (1) and (2), we get BE = DF and BD = EF Hence, BDEF is a parallelogram. (ii) Now, AB = 2EF = 2 × 4.8 = 9.6cm15. In triangle ABC, AD is the median, and DE, drawn parallel to side BA, meets AC at point E. Show that BE is also a median.
Solution:
In ∆ABC, we have AD is the median of BC D is the mid-point of BC Given that DE || BA So, by the converse of the mid-point theorem, DE bisects AC ⇒ E is the mid-point of AC And, BE is the median of AC Hence, BE is also a median.16. In ∆ ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q. Show that BE: EQ = 3:1.
Solution:
Construction: Draw DY || BQ In ∆BCQ and ∆DCY, we have ∠BCQ = DCY [Common] ∠BQC = ∠DYC [Corresponding angles] So, ∆BCQ ~ ∆DCY by AA similarity criterion Thus, BQ/DY = BC/DC = CQ/CY [Corresponding sides are proportional] BQ/DY = 2 … (i) Similarly, ∆AEQ ~ ∆ADY EQ/DY = AE/ED = ½ [E is the mid-point of AD] ⇒ EQ/DY = ½ … (ii) On dividing (i) by(ii), we get BQ/EQ = 4 BQ = 4 EQ BE + EQ = 4EQ BE = 3EQ Therefore, BE/EQ = 3/117. In the given figure, M is the mid-point of AB and DE, whereas N is the mid-point of BC and DF. Show that: EF = AC.
Solution:
In ∆EDF, we have M is the mid-point of AB and N is the mid-point of DE So, MN = ½ EF (By mid-point theorem) EF = 2MN … (i) In ∆ABC, we have M is the mid-point of AB and N is the mid-point of BC MN = ½ AC (By mid-point theorem) AC = 2MN … (ii) From (i) and (ii), we get EF = ACICSE Class 9 Maths Selina Solutions Chapter 12 Exercise 12B
1. Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
Solution:
According to the equal intercept theorem, as CD = DE ⇒ AB = BC and EF = GF Thus, (i) BC = AB = 7.2cm (ii) GE = EF + GF = 2EF = 2 × 4 = 8 cm Since B, D, and F are the midpoints and AE || BF || CG Therefore, AE = 2BD and CG = 2DF (iii) AE = 2BD = 2 × 4.1 = 8.2 cm (iv) DF = ½ CG = ½ × 11 = 5.5 cm2. In the figure, given below, 2AD = AB, P is the mid-point of AB, and Q is the mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
Solution:
Given, AD = AP = PB as 2AD = AB and P is the midpoint of AB (i) In ∆DPR, we have A and Q are the midpoints of DP and DR Therefore, AQ || PR Now, as PR || BS ∴ AQ || BS (ii) In ∆ABC, P is the midpoint, and PR || BS Therefore, R is the midpoint of BC Now, in ∆BRS and ∆QRC, we have ∠BRS = ∠QRC BR = RC ∠RBS = ∠RCQ ∴ ∆BRS ≅ ∆QRC by SAS Congruence criterion Hence, by CPCT QR = RS Thus, DS = DQ + QR + RS = QR + QR + RS = 3RS3. The side AC of a triangle ABC is produced to point E so that CE = ½ AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
(i) 3DF = EF (ii) 4CR = AB.
Solution:
Let’s consider the figure below: In this case, DP is parallel to AB and D is the midpoint of BC. Consequently, PD = ½ AB, and P is the midway of AC. (i) Again, in ∆AEF we have AE || PD || CR and AP = 1/3 AE Therefore, DF = 1/3 EF ⇒ 3DF = EF – Hence proved (ii) In ∆PED, we have PD || CR , and C is the midpoint of PE So, CR = ½ PD Now, PD = ½ AB ½ PD = ¼ AB CR = ¼ AB 4CR = AB – Hence proved4. In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
(i) M, A, and N are collinear.
(ii) A is the mid-point of MN.
Solution:
The figure is shown below: (i) In ∆BPC and ∆MPA, we have ∠BPC = ∠APN [Vertically opposite angle] BP = MP PC = PA ∴ ∆BPC ≅ ∆MPA by SAS congruence postulate Thus, by CPCT ∠PCB = ∠PAM … (1) And, BC = AM … (2) Similarly, Considering ∆CQB and ∆NQA, we have ∠QBC = ∠QAN … (3) And, BC = AN … (4) Now, by angle sum property of ∆ABC ∠ABC + ∠ACB + ∠BAC = 180 o ⇒ ∠QBC + ∠PCB + ∠BAC = 180 o ∠QAN + ∠PAM + ∠BAC = 180 o [From (1) and (3)] Therefore, it’s a straight angle, and M, A, and N must be collinear. (ii) Now, from (2) and (4) we have AM = AN Hence, A is the midpoint of MN.5. In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
Solution:
The figure is shown below: We have, EF||AB and E is the midpoint of BC Therefore, F is the midpoint of AC And, EF = BD as D is the midpoint of AB Now, as BE || DF BE = DF as E is the midpoint of BC. Therefore, BEFD is a parallelogram.6. In a parallelogram ABCD, E, and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that:
(i) Triangles HEB and FHC are congruent
(ii) GEHF is a parallelogram.
Solution:
The figure is shown below: (i) In ∆HEB and ∆HCF, we have BE = FC [Given] ∠EHB = ∠FHC [Vertically opposite angles] ∠HBE = ∠HFC [Alternate angles] ∴ ∆HEB ≅ ∆HCF by ASA congruence criterion ∴ EH = CH, BH = FH (ii) Similarly, AG = GF and EG = DG … (1) In ∆ECD, we have F and H are the midpoints of CD and EC respectively Therefore, HF || DE and HF = ½ DE … (2) From (1) and (2), we get HF = EG and HF || EG Similarly, we can show EH = GF and EH || GF Therefore, GEHF is a parallelogram.7. In triangle ABC, D, and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet side BC at points M and N respectively. Prove that: BM = MN = NC.
Solution:
The figure is shown below: In ∆AEG, we have D is the midpoint of AE and DF || EG || BC Therefore, F is the midpoint of AG ⇒ AF = GF … (1) Again, we have DF || EG || BC and DE = BE Therefore, GF = GC … (2) From (1) and (2), we get AF = GF = GC Similarly, as GN || FM || AB and AF = GF Therefore, BM = MN = NC – Hence proved.8. In triangle ABC; M is the mid-point of AB, N is the mid-point of AC and D is any point in base BC. Use the intercept theorem to show that MN bisects AD.
Solution:
The figure is shown below As M and N are the midpoint of AB and AC respectively and MN || BC Then according to the intercept theorem, we have AM = BM, And therefore, AX = DX. – Hence proved9. If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at a right angle.
Solution:
The figure is shown below: Let ABCD be a quadrilateral where P, Q, R, and S are the midpoints of AB, BC, CD, and DA. And, PQRS is a rectangle Diagonal AC and BD intersect at point O. Required to show: AC and BD intersect at right angle. Proof: As PQ || AC, ⇒ ∠AOD = ∠PXO [Corresponding angles] … (1) Again, as BD||RQ, ⇒ ∠PXO = ∠RQX = 90 o [Corresponding angle and angle of rectangle] … (2) From (1) and (2), we get ∠AOD = 90 o Similarly, ∠AOB = ∠BOC = ∠DOC = 90 o Therefore, diagonals AC and BD intersect at a right angle – Hence proved.10. In triangle ABC; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm, and BC = 18 cm, find the perimeter of the parallelogram BDEF.
Solution:
The figure is shown below: As E is the midpoint of AC and EF||AB, we have Thus, F is the midpoint of BC and 2DE = BC or DE = BF Again, as D and E are midpoints, we have DE||BF and EF = BD Hence, BDEF is a parallelogram. Now, BD = EF = ½ AB = ½ ×16 = 8cm BF = DE = ½ BC = ½ ×18 = 9cm Therefore, perimeter of BDEF = 2(BF + EF) = 2(9 + 8) = 34cm11. In the given figure, AD and CE are medians and DF||CE. Prove that: FB = ¼ AB
Solution:
Considering that DF || CE and AD and CE are medians Based on the midpoint theorem, we are aware that When two lines are parallel and a segment begins at one side's midway, the other point meets at the other side's midpoint. Consider ∆BEC, Given that DF || CE and D is the midpoint of BC So, F must be the midpoint of BE ⇒ FB = ½ BE … (i) But, BE = ½ AB On substituting the value of BE in (i), we get FB = ¼ AB – Hence Proved12. In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
Solution:
Given ABCD is parallelogram, ⇒ AD = BC and AB = CD (i) Now, in ∆APB Given, EC is parallel to AP and E is the midpoint of side AB So, by the midpoint theorem, C is the midpoint of BP So, BP = 2BC But, BC = AD as ABCD is a parallelogram. Hence, BP = 2AD (ii) In ∆APB, we have AB || OC as ABCD is a parallelogram So, by the midpoint theorem O is the midpoint of the AP Hence Proved.13. In trapezium ABCD, sides AB and DC are parallel to each other. E is the mid-point of AD and F is the mid-point of BC. Prove that: AB + DC = 2EF.
Solution:
In trapezium ABCD, we have E and F are the midpoints of sides AD and BC respectively We know that, AB = GH = IJ From the midpoint theorem, we have EG = ½ DI and HF = ½ JC Now, consider the L.H.S, we have AB + CD = AB + CJ + JI + ID = AB + 2HF + AB + 2EG So, AB + CD = 2(AB + HF + EG) = 2(EG + GH + HF) = 2EF ∴ AB + CD = 2EF – Hence Proved.14. In ΔABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
Solution:
Given, that ΔABC and AD are the median So, D is the midpoint of side BC Also, given DE || AB The midway theorem states that E must be AC's midway. Thus, the median is always the line that connects the vertex with the opposite side's midway. Therefore, BE is also ΔABC's median.15. Adjacent sides of a parallelogram are equal and one of the diagonals is equal to any one of the sides of this parallelogram. Show that its diagonals are in the ratio √ 3:1.
Solution:
It is a rhombus if the parallelogram's neighboring sides are equal. At this point, a rhombus's diagonals are perpendicular to one another and bisect one another. Assume that x and y are the diagonals' lengths. The length of the diagonal should match the rhombus's sides. Now, in right-angled ΔBOC By Pythagoras theorem, OB 2 + OC 2 = BC 2 (y/2) 2 + (x/2) 2 = y 2 x 2 /4 = y 2 – y 2 /4 x 2 /4 = (4y 2 – y 2 )/4 x 2 /4 = 3y 2 /4 x 2 = 3y 2 x 2 /y 2 = 3/1 x/y = √3/1 Thus, the diagonals are in the ratio √3: 1Benefits of ICSE Class 9 Maths Selina Solutions Chapter 12
Selina Solutions for ICSE Class 9 Maths Chapter 12 "Mid Point and Its Converse" offer several benefits for students studying this topic. Here are some key advantages:Comprehensive Coverage : Selina Solutions provide a thorough explanation of concepts related to midpoints and their properties. They cover all essential topics, ensuring that students have a complete understanding of the chapter.
Step-by-Step Solutions : Each problem in Selina Solutions is solved step-by-step, making it easier for students to follow and understand the reasoning behind each solution. This helps in grasping the methodology required to solve similar problems.
Clarity and Structure : The solutions are structured in a clear and organized manner. This helps students develop a systematic approach to problem-solving, which is crucial for exams.
Practice Material : Selina Solutions typically include a variety of practice questions, ranging from basic to advanced levels. This allows students to gauge their understanding and practice extensively.
Additional Resources : Apart from solutions to textbook exercises, Selina Solutions often provide additional notes, tips, and shortcuts that can aid students in understanding concepts more effectively.
Exam Preparation : By using Selina Solutions, students can familiarize themselves with the types of questions likely to appear in exams. This helps in building confidence and reducing anxiety during exams.
ICSE Class 9 Maths Selina Solutions Chapter 12 FAQs
What is the converse of the midpoint theorem Class 9?
What is the mid point theorem Class 9 Chapter 9?
What is the intercept theorem Class 9?
What is the formula of the midpoint theorem?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
