
ICSE Class 9 Maths Selina Solutions Chapter 15: Here are the ICSE Class 9 Maths Selina Solutions Chapter 15 Construction of Polygons. Since the concepts taught in Class 9 are carried over into Class 10, Class 9 is one of the most crucial years in a student's life.
It is recommended that students complete the exercises in every chapter of the Selina book to achieve high scores on the mathematics exam for Class 9. These Selina maths solutions for class 9 aid students in better comprehending the material covered.ICSE Class 9 Maths Selina Solutions Chapter 15 Overview
ICSE Class 9 Maths Selina Solutions Chapter 15 PDF
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 15 in detail. This chapter will help you to clear all your doubts regarding the chapter Inequalities. Students are advised to prepare from these ICSE Class 9 Maths Selina Solutions Chapter 15 before the examinations to perform better.ICSE Class 9 Maths Selina Solutions Chapter 15 PDF
ICSE Class 9 Maths Selina Solutions Chapter 15 Contruction of Polygons
Below we have provided ICSE Class 9 Maths Selina Solutions Chapter 15 -Construct a quadrilateral ABCD, when:
1. AB = 3.2 cm, BC = 5.2 cm, CD = 6.2 cm, DA = 4.2 cm and BD = 5.2 cm.
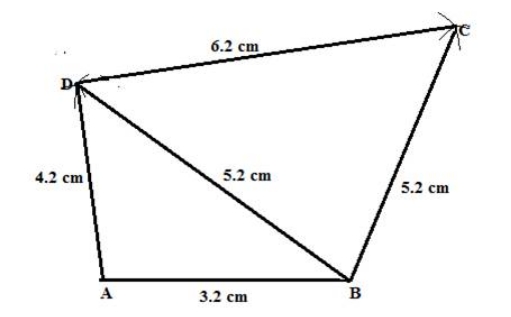
Solution:
Steps of construction: 1. Draw AB = 3.2 cm. 2. With A as the centre and radius of 4.2 cm, draw an arc at D and with B as the centre and radius of 5.2 cm draw an arc to intersect at D. 3. Now, join AD and DB. 4. With D and B as centres and radii 6.2 cm and 5.2 cm respectively, draw arcs cutting each other at C. 5. Lastly, join BC and DC. Thus, ABCD is the required quadrilateral.2. AB = 7.2 cm, BC = 5.8 cm, CD = 6.2 cm, AD = 4.3 cm and angle A = 75 o .
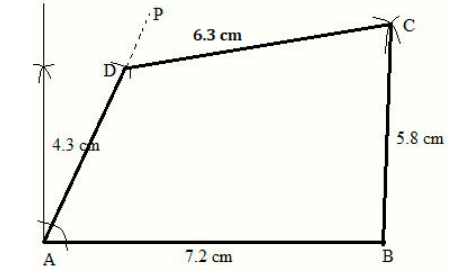
Solution:
Steps of construction: 1. Draw AB = 7.2 cm. 2. At A construct AP such that ∠A = 75 o . 3. Cut off AD = 4.3 cm from AP. 4. With D and B as centres and radii 6.2 cm and 5.8 cm respectively, draw arcs cutting each other at C. 5. Now, join DC and BC. Thus, ABCD is the required quadrilateral.3. Angle A = 90 o , AB = 4.6 cm, BD = 6.4 cm, AC = 6.0 cm and CD = 4.2 cm.
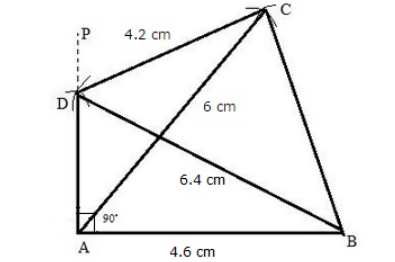
Solution:
Steps of construction: 1. Draw AB = 4.6 cm. 2. At A, construct AP such that ∠A = 90°. 3. With B as the centre and a radius of 6.4 cm, draw an arc intersecting AP at D. 4. Taking D and A as centres and radii 4.2 cm and 6 cm respectively, draw arcs cutting each other at C. 5. Now, join BD, AC and CB. Thus, ABCD is the required quadrilateral.4. AB = 3.8 cm, AC = 4.8 cm, AD = 2.8 cm, angle A = 105 o and angle B = 60 o .
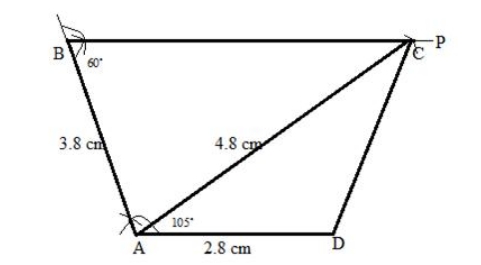
Solution:
Steps of construction: 1. Draw AD = 2.8 cm. 2. Construct AB = 3.8 cm such that ∠A = 105 o . 3. Draw BP such that ∠B = 60 o . 4. Now, taking A as the centre and radius of 4.8 cm, draw an arc-cutting BP at C. 5. Join AC and AD. Thus, ABCD is the required quadrilateral.5. BC = 7.5 cm AC = 5.8 cm, AD = 3.6 cm, CD = 4.2 cm and angle A = 120 o .
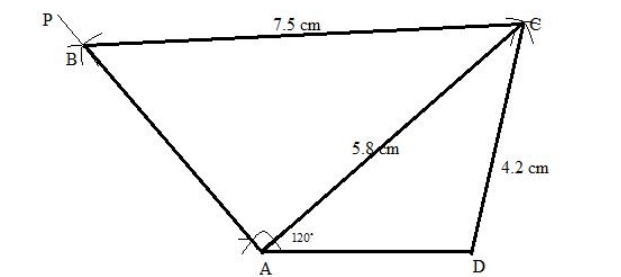
Solution:
Steps of construction: 1. Draw AD = 3.6 cm. 2. Construct AP such that ∠A = 120 o . 3. Taking A and D as the centres and radii 5.8 cm and 4.2 cm, draw arcs cutting each other at C. 4. Join AC and CD. 5. Now, taking C as the centre and radius of 7.5 cm, draw an arc to intersect AP at B. 6. Join CB. Thus, ABCD is the required quadrilateral.6. AD = AB = 4 cm, BC = 2.8 cm, CD = 2.5 cm and angle BAD = 45 o .
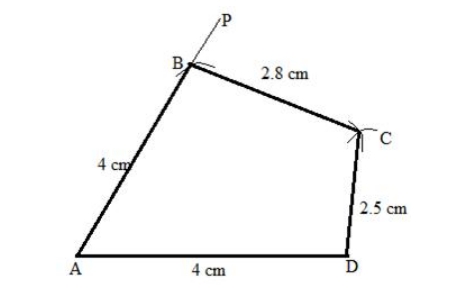
Solution:
Steps of construction: 1. Draw AD = 4 cm. 2. Construct AP such that ∠A = 45 o . 3. Taking A as the centre with a radius of 4 cm, draw an arc-cutting AP at B. 4. Now, with B and D as centres and radii 2.8 cm and 2.8 cm respectively, draw arcs cutting each other at C. 5. Join BC and CD. Thus, ABCD is the required quadrilateral.7. AB = 6.3 cm, BC = CD = 4.2 cm and ∠ABC = ∠BCD = 90 o .
Solution:
Steps of construction: 1. Draw AB = 6.3 cm. 2. Construct BP such that ∠ABP = 90 o . 3. Taking B as the centre and radius of 4.2 cm, draw an arc to cut AP at C. 4. Now, with C as the centre and radii 4.2 cm, construct CD such that ∠BCD = 90 o . 5. Join AD. Thus, ABCD is the required quadrilateral.Construct a parallelogram ABCD, when:
8. AB = 4.4 cm, AD = 6.2 cm and AC = 4.8 cm.
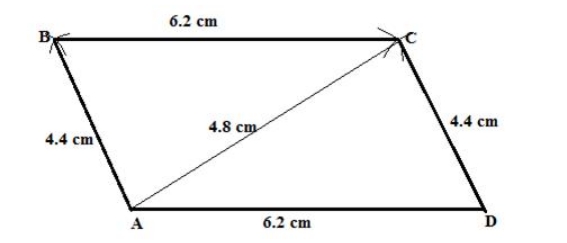
Solution:
Steps of construction: 1. Draw AD = 6.2 cm. 2. Taking A and D as centres and radii 4.8 cm and 4.4 cm respectively, draw arcs cutting each other at C. 3. Join AC and CD. 4. Now, with A and C as centres and radii 4.4 cm and 6.2 cm respectively, draw arcs cutting each other at B. 5. Join AB and BC. Thus, ABCD is the required parallelogram.9. Diagonal AC = 6.4 cm, diagonals BD = 8.2 cm and angle between the diagonals = 60 o .
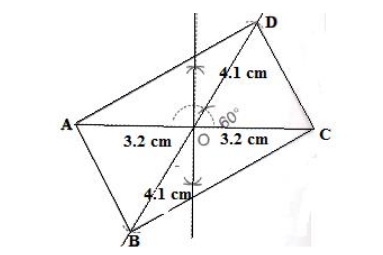
Solution:
Steps of construction: 1. Draw AC = 6.4 cm. 2. Construct BOD such that ∠DOC = 60 o and OB = OD = ½ BD = ½ x 8.2 = 4.1 cm. 3. Now, join AB, BC, CD and DA. Thus, ABCD is the required parallelogram.10. AB = 5.8 cm, diagonal AC = 8.2 cm and diagonal BD = 6.2 cm.
Solution:
Steps of construction: 1. Draw AB = 5.8 cm. 2. As the diagonals of a parallelogram bisect each other. Construct OAB such that: OA = ½ AC = ½ x 8.2 cm = 4.1 cm OB = ½ BD = ½ x 6.2 cm = 3.1 cm 2. Produce AO up to C, such that OC = OA = 4.1 cm and BO up to D, such that DO = OB = 3.1 cm. 3. Now, join AD, DC and CB. Thus, ABCD is the required parallelogram.11. AB = 6.0 cm, AD = 5.0 cm and ∠A = 45 o .
Solution:
Steps of construction: 1. Draw AB = 6 cm. 2. Construct AD = 5 cm such that ∠BAD = 45 o . 3. Taking D and B as the centres and radii 6 cm and 5 cm, draw arcs cutting each other at C. 4. Now, join DC and BC. Thus, ABCD is the required parallelogram.12. Base AB = 6.5 cm, BC = 4 cm and the altitude corresponding to AB = 3.1 cm.
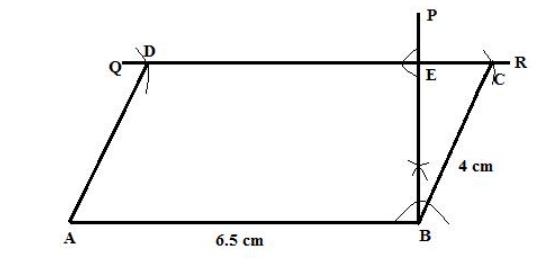
Solution:
Steps of construction: 1. Draw AB = 6.5 cm. 2. At B, construct BP ⊥ AB. 3. Cut off BE = 3.1 cm from BP. 4. At E, construct a perpendicular to BP to obtain QR parallel to AB. 5. Now, taking B as the centre and radius of 4 cm, draw an arc which cuts QR at C. 6. With A as a centre and radius 4 cm, draw an arc which cuts QR at D. Thus, ABCD is the required parallelogram.13. AB = 4.5 cm, ∠B = 120 o and the distance between AB and DC = 3.0 cm.
Solution:
Steps of construction: 1. Draw AB = 4.5 cm. 2. At B, construct BP ⊥ AB. 3. Cut off BE = 3 cm, from BP. 4. At E, draw a perpendicular to BP to obtain QR parallel to AB. 5. Now, taking B as the centre draw an arc which cuts QR at C such that ∠B = 120 o . 6. With A as a centre and radius BC, draw an arc which cuts QR at D. 7. Join AD and BC. Thus, ABCD is the required parallelogram.14. Base BC = 5.6 cm, diagonal BD = 6.5 cm and altitude = 3.2 cm.
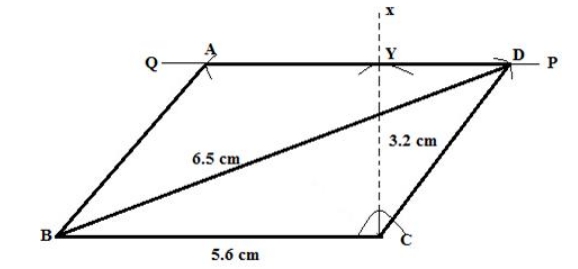
Solution:
Steps of construction: 1. Draw BC = 5.6 cm. 2. At C, construct CX ⊥ BC. 3. Taking C as the centre and radius 3.2 cm draw an arc to cut CX at Y. 4. At Y, draw a straight-line PQ parallel to BC. 5. Now, taking B as the centre and radius 6.5 cm, draw an arc to meet PQ at D. 6. With D as a centre and radius to 5.6 cm, draw an arc to meet PQ at A. 7. Join BA, BD and CD. Thus, ABCD is the required parallelogram.Construct a rectangle ABCD, when
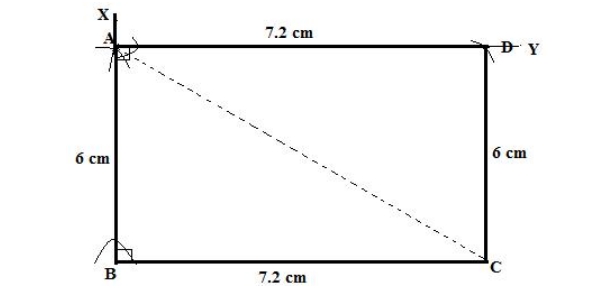
15. Its sides are 6.0 cm and 7.2 cm.
Solution:
We know that each angle of a rectangle is 90 o and opposite sides are equal. Steps of construction: 1. Draw BC = 7.2 cm. 2. Taking B as the centre, draw a line BX such that ∠B = 90 o . 3. Now, with B as the centre and radius 6 cm draw an arc to cut BX at A. 4. At A, construct a line AY parallel to BC. 5. Taking A as the centre and radius 7.2 cm draw an arc to cut AY at D. 6. Join CD. Thus, ABCD is the required rectangle.16. One side = 4 cm and one diagonal is 5 cm. Measure the length of other side.
Solution:
Steps of construction: 1. Draw BC = 4 cm. 2. Taking C as the centre and radius 5 cm, draw an arc at A such that ∠ABC = 90 o . 3. Join AB and AC. 4. Now, with A as a centre and radius 4 cm, draw an arc at D such that ∠ADC = 90 o . 5. Join AD and CD. Thus, ABCD is the required rectangle.17. One diagonal = 6.0 cm and the acute angle between the diagonals = 45 o .
Solution:
Steps of construction: 1. Draw AC = 6 cm. 2. Now, bisect AC at O. 3. At O, construct ∠XOC = 45° and produce XO to Y. 4. Cut OB = OD = 3 cm (i.e., half the diagonal 6 cm) 5. Join AB, CB, AD and CD. Thus, ABCD is the required rectangle18. Area = 24 cm 2 and base = 4.8 cm.
Solution:
Given, Base = 4.8 cm and area = 24 cm 2 We know that, area of rectangle = base x height So, 24 = 4.8 x height Height = 24/4.8 = 5 cm The rectangle with base = 4.8 cm and height = 5 cm is constructed as below. Steps of construction: 1. Draw base, AB = 4.8 cm. 2. Taking A and B as a centres and radii 5 cm each, draw arcs at D and C. 3. Now, join AD, BC and DC. Thus, ABCD is the required rectangle.19. Area = 36 cm 2 and height = 4.5 cm.
Solution:
Given, Height = 4.5 cm and area = 36 cm 2 We know that, area of rectangle = base x height So, 36 = base x 4.5 Base = 36/4.5 = 8 cm The rectangle with base = 8 cm and height = 4.5 cm is constructed as below. Steps of construction: 1. Draw base, AB = 8 cm. 2. Taking A and B as a centres and radii 4.5 cm each, draw arcs at D and C. 3. Join AD, BC and DC. Thus, ABCD is the required rectangle.Construct a trapezium ABCD, when:
20. AB = 4.8 cm, BC = 6.8 cm, CD = 5.4 cm, angle B = 60 o and AD || BC.
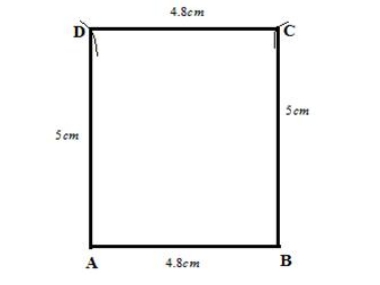
Solution:
Steps of construction: 1. Draw BC = 6.8 cm. 2. Taking B as the centre and radius 4.8 cm, draw an arc at A such that ∠B = 60 o . 3. At A, draw a line AP such that AP || BC. 4. With C as the centre and radius 5.4 cm, draw an arc AP to cut at D. 5. Now, join AB and CD. Thus, ABCD is the required trapezium.21. AB = CD = 3.2 cm, BC = 6.0 cm, AD = 4.1 cm and AD // BC.
Solution:
Steps of construction: 1. Draw BC = 6 cm. 2. Cut off BE = AD = 4.1 cm from BC. 3. Construct triangle DEC such that DE = AB = 3.2 cm and CD = 3.2 cm. 4. Taking B and D as the centres and radii 3.2 cm and 4.1 cm respectively, draw arcs cutting each other at A. 5. Join AB and AD. Thus, ABCD is the required trapezium.Construct a rhombus ABCD, when:
22. It’s one side = 6 cm and ∠ A = 60 o .
Solution:
Steps of construction: 1. Draw AB = 6 cm. 2. At A, construct ∠BAP = 60 o . 3. From AP, cut off D such that AD = 6 cm. 4. At B, construct BQ || AD. 5. At D, construct DC || AB to cut BQ at C. Thus, ABCD is the required rhombus.23. One side = 5.4 cm and one diagonals is 7.0 cm.
Solution:
Steps of construction: 1. Draw AC = 7 cm. 2. Taking A as the centre and radius 5.4 cm, draw an arc extending on both sides of AC. 3. Taking C as the centre and radius 5.4 cm, draw an arc extending on both sides of AC to cut the first arc at B and D. 4. Now, join AB, BC, CD and DA. Thus, ABCD is the required rhombus.24. Diagonal AC = 6.3 cm and diagonal BD = 5.8 cm.
Solution:
Steps of construction: 1. Draw AC = 6.3 cm. 2. Construct the perpendicular bisector of AC which cuts AC at O. 3. Cut off OD and OB on the perpendicular bisector such that, OD = OB = ½ BD = ½ x 5.8 = 2.9 cm 4. Join AB, BC, CD and DA. Thus, ABCD is the required rhombus.25. One side = 5.0 cm and height = 2.6 cm.
Solution:
Steps of construction: 1. Draw AB = 5 cm. 2. At B, construct BP ⊥ AB. 3. Cut off BE = 2.6 cm from BP. 4. At E, draw perpendicular to CP so that QR || AB. 5. Taking A and B as the centres and radii 5 cm each, draw arcs cutting QR at D and C. Thus, ABCD is the required rhombus.26. ∠ A = 60 o and height = 3.0 cm.
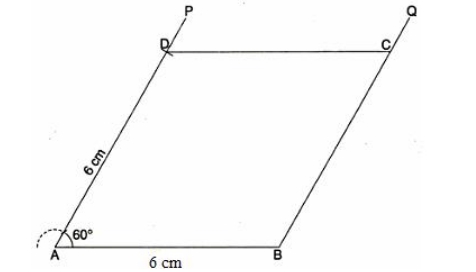
Solution:
Steps of construction: 1. Draw a line AP. 2. Now, draw AF such that ∠A = 60 o . 3. At S, construct a perpendicular SE = 3 cm such that it cuts AF at D. 4. Through D draw a line QR parallel to AP. 5. Taking the radius same as AD, draw an arc at B on AP. 6. Now, at B taking radius same as AD and AB, draw arcs cutting each other at C. 7. Join BC. Thus, ABCD is the required rhombus.27. Diagonal AC = 6.0 cm and height = 3.5 cm.
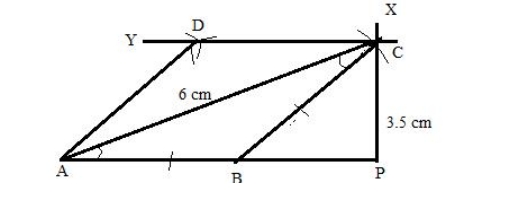
Solution:
Steps of construction: 1. Draw the AP line. 2. Draw arcs that meet at C using A and P as the centres and their respective radii of 6 and 3.5 cm. 3. At this point, draw BC so that BC equals AB. 4. Draw a line parallel to AP at C that is CY. 5. Draw arcs that intersect at D at points C and A, using the same radius as AB. 6. Assist AD. Therefore, the necessary rhombus is ABCD.Construct a square ABCD, when:
28. One side = 4.5 cm.
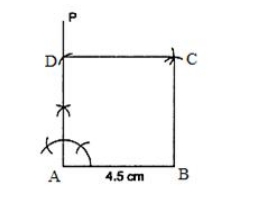
Solution:
Steps of construction: 1. Draw AB, or 4.5 cm. 2. Construct AP ⊥ AB. 3. Cut off AP by AD, or 4.5 cm. 4. Draw an arc with B as the centre and a radius of 4.5 cm. 5. Now draw another arc that cuts through the previous one at C, using D as the centre and a radius of 4.5 cm. 6. Assist CD and BC. Therefore, the necessary square is ABCD.29. One diagonal = 5.4 cm.
Solution:
We know that, the diagonals of a square are equal and bisect each other at right angles. Steps of construction: 1. Draw AC = 5.4 cm. 2. Construct the right bisector XY of AC, meeting AC at O. 3. Now, from O, set off OB = ½ (5.4) = 2.7 cm along OY and OD = 2.7 cm along OX. 4. Join AB, BC, CD and DA. Thus, ABCD is the required square.30. Construct a square ABCD, when perimeter = 24 cm.
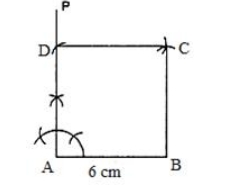
Solution:
Given, perimeter of the square = 24 cm We know that, Perimeter of square, P = 4a Where, a is the length of each side. So, 24 = 4a a = 24/4 = 6 cm Therefore, the sides of the squares are of length 6 cm. Steps of construction: 1. Draw AB, or 6 cm. 2. Compose AP ⊥ AB. 3. Cut AD off from AP by 6 cm. 4. Draw an arc with B as the middle and a radius of 6 cm. 5. Now draw another arc that cuts through the previous one at C, using D as the centre and a radius of 6 cm. 6. Assist CD and BC. Therefore, the necessary square is ABCD.31. Construct a rhombus, having given one side = 4.8 cm and one angle = 75 o .
Solution:
Steps of construction: 1. Draw a line AB = 4.8 cm. 2. At A, draw AX such that ∠BAX = 75 o . 3. Taking A as the centre and radius = AB, cut off an arc at D on AX. 4. Now, taking D and B as centers and radius same as AB, cut off arcs which will intersect at C. 5. Join CD and CB. Thus, ABCD is the required rhombus.32. (i) Construct a regular hexagon of side 2.5 cm.
(ii) Construct a regular hexagon of side 3.2 cm.
Solution:
The length of side of regular hexagon is equal to the radius of its circumcircle. (i) Steps of construction: 1. Sketch a 2.5 cm-radius circle. 2. Draw arcs that cut the circle at B and F, using any point A as the centre and radii of 2.5 cm on the circumference. 3. Draw two arcs with the same radius = 2.5 that intersect the circle at C and E, respectively, using B and F as the centres. 4. Next, draw another arc with a radius of 2.5 cm, cutting the circle at point D, using C or E as the centre. In this manner, the circle's diameter is split into six equal sections. 5. Assist EF, FA, DE, CD, AB, and BC. Therefore, the necessary hexagon is ABCDEF.33. Using ruler and compasses only, construct the quadrilateral ABCD, having given AB = 5 cm, BC = 2.5 cm, CD = 6 cm. angle BAD = 90 o and the diagonal AC = 5.5 cm.
Solution:
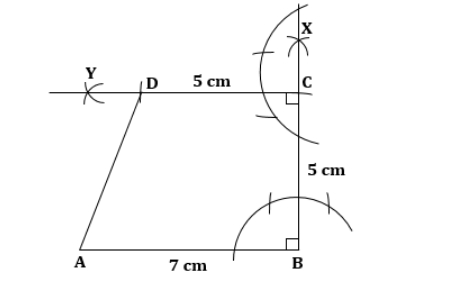 Steps of construction:
1. Draw AB, or 5 cm.
2. Create ∠XAB = 90 now.
3. Draw arcs that intersect at C, using A and B as the centres and the corresponding radii of 2.5 and 5.5 cm.
4. Assist AC and BC.
5. Next, draw arcs at D on AXE using C as the centre and a radius of 6 cm.
Therefore, the necessary quadrilateral is ABCD.
Steps of construction:
1. Draw AB, or 5 cm.
2. Create ∠XAB = 90 now.
3. Draw arcs that intersect at C, using A and B as the centres and the corresponding radii of 2.5 and 5.5 cm.
4. Assist AC and BC.
5. Next, draw arcs at D on AXE using C as the centre and a radius of 6 cm.
Therefore, the necessary quadrilateral is ABCD.
34. Using ruler and compasses only, construct a trapezium ABCD, in which the parallel sides AB and DC are 3.3 cm apart; AB = 4.5 cm, angle A = 120 o BC = 3.6 cm and angle B is obtuse.
Solution:
Steps of construction: 1. Draw AB = 4.5 cm. 2. Construct ∠BAS = 120 o and draw EA ⊥ AB such that AX = 3.3 cm. 3. At X, draw a line QR which is parallel to AB that cuts AS at D. 4. At B, draw an arc of radius 3.6 cm to cut PQ at C. 5. Now, join CB. Thus, ABCD is the required trapezium.35. Using ruler and compasses only, construct the quadrilateral ABCD, having given AB = 5 cm, BC = 2.5 cm CD = 6 cm, ∠ BAD = 90 o and diagonal BD = 5.5 cm.
Solution:
Steps of construction: 1.Draw AB = 5cm. 2. At A, draw a line AY such that ∠A = 90 o . 3. With B as the centre and radius 5.5 cm, draw an arc at D on AY. 4. taking D and B as the centre and radii 6 cm and 2.5 cm respectively, draw arcs cutting each other at C. 5. Now, join DC and BC. Thus, ABCD is the required quadrilateral.36. Using ruler and compasses only, construct a parallelogram ABCD using the following data: AB = 6 cm, AD = 3 cm and ∠DAB = 45 o . If the bisector of ∠DAB meets DC at P, prove that ∠APB is a right angle.
Solution:
Steps of construction: 1. Draw AB = 6 cm. 2. Taking A as the centre and radius draw a line AX such that ∠BAX = 45 o . 3. With A as the centre and radius 3 cm, draw an arc on AD. 4. Now, taking D and B as a centres and radii 6 cm and 3 cm respectively, draw arcs cutting each other at C. 5. Join DC and BC. Thus, ABCD is the required parallelogram. Here, we have∠ PAB = ∠ APD … [Alternate angles]
∠ CPB = ∠ PBA … [Alternate angles]
Now,∠ DPA + ∠ APB + ∠ CPB = 180 o …… (i)
Also, considering ∆APB,∠ PAB + ∠ PBA + ∠ APB = 180 o …… (ii)
Hence, from (i) and (ii)∠ APB = 90 o
– Hence proved.37. The perpendicular distance between the pair of opposite sides of a parallelogram are 3 cm and 4 cm, and one of its angles measures 60 o . Using ruler and compasses only, construct the parallelogram.
Solution:
Steps of construction: 1. Create a baseline AQ using a haphazard measurement. 2. Build a perpendicular that cuts the line AQ at P. 3. Draw an arc on the perpendicular bisector above the line, using P as the centre and radius = 4 cm in the compass. Draw a line through this arc that is parallel to line AQ. 4. Create a 60-degree angle at point A, then draw the line that intersects the sketched line at point D. 5. Create a perpendicular to line AD now.38. Draw parallelogram ABCD with the following data:
AB = 6 cm, AD = 5 cm and ∠DAB = 45 o .
Let AC and DB meet in O and let E be the mid-point of BC. Join OE. Prove that:
(i) OE || AB (ii) OE = ½ AB.
Solution:
Steps of construction: First draw a line AB = 6 cm. Then draw an angle of measure 45 o at point A such that ∠ DAB = 45 o and AD = 5 cm. Now, draw a line CD = 6 cm parallel to the line AB . Join BC to construct the parallelogram. Now, we are to prove that OE || AB and OE = ½ AB. Since O is the midpoint of AC and E is the midpoint of BC . Hence, the line is parallel to AB and OE = ½ AB.39. Using ruler and compasses only, construct a rectangle each of whose diagonals measure 6 cm and the diagonals interest at an angle of 45 o .
Solution:
Steps of construction: 1. First, draw a line AC = 6 cm. 2. Then draw the perpendicular bisector of AC through O . 3. At O, draw an angle of measure 45 o . Then produce OD = 3 cm and OB = 3 cm. 4. Join AD , AB , BC and CD to form the rectangle. Thus, ABCD is the required rectangle.Benefits of ICSE Class 9 Maths Selina Solutions Chapter 15
Studying from ICSE Class 9 Maths Selina Solutions Chapter 15 on the Construction of Polygons, offers several benefits:Structured Approach : ICSE Class 9 Maths Selina Solutions Chapter 15 provide a step-by-step breakdown of each construction method. This structured approach helps students understand the logical progression of constructing polygons.
Clarity and Explanation : The ICSE Class 9 Maths Selina Solutions Chapter 15 offer clear explanations alongside diagrams that illustrate each construction method. This visual aid enhances comprehension, making it easier for students to grasp the concepts.
Practice Problems : ICSE Class 9 Maths Selina Solutions Chapter 15 typically include practice problems that reinforce the concepts learned in the chapter. These problems vary in difficulty, allowing students to gradually build their confidence and proficiency in polygon construction.
Comprehensive Coverage : The ICSE Class 9 Maths Selina Solutions Chapter 15 cover all the essential construction techniques required at the Class 9 level, ensuring that students are well-prepared for exams and practical applications.
Supplementary Resources : Apart from the textbook, ICSE Class 9 Maths Selina Solutions Chapter 15 often include additional resources such as tips, notes, and alternative methods of solving problems. These resources provide a more holistic learning experience.
ICSE Class 9 Maths Selina Solutions Chapter 15 FAQs
Which is hardest chapter in maths class 9?
Is 9th class toughest?
Who is known as the father of maths?
Is class 9 stressful?










