Linear Equations in Two Variables Formula, Definition,

A l inear Equations in two Variables is characterized by both variables having an exponent of 1. When addressing a system of equations with two variables, the potential outcomes encompass a distinct solution, a lack of solutions, or an infinite number of solutions. Such a linear equation system could encompass 'n' variables. In the process of solving linear equations with 'n' variables, a crucial rule to remember is that the number of equations should match 'n' to enable the determination of variable values.

Linear equations in two variables adopt the format (or can be transformed into the format) y = mx + b, where 'm' signifies the slope and 'b' represents the y-intercept. They are classified as first-order equations. For instance, y = 2x + 3 and 2y = 4x + 9 exemplify two-variable linear equations.

What are Linear Equations in Two Variables?

Linear equations involving two variables are characterized by each variable having the highest exponent of 1. These equations can yield one, zero, or an infinite number of solutions. The typical structure of a two-variable linear equation is ax + by + c = 0, where 'x' and 'y' represent the variables. Solutions are often presented as ordered pairs like (x, y). The graphical depiction of pairs of linear equations in two variables results in the formation of two straight lines that can be:

• Intersecting lines
• Parallel lines
• Coincident lines

Forms of Linear Equations in Two Variables

A linear equation involving two variables can be expressed in various formats, including standard form, intercept form, and point-slope form. For instance, the equation 2x + 3y = 9 can be represented in each of these forms: 2x + 3y - 9 = 0 (standard form), y = (-2/3)x + 3 (slope-intercept form), and y - 5/3 = -2/3(x + (-2)) (point-slope form). Refer to the provided image illustrating these three ways of representing linear equations in two variables, accompanied by examples.

A system of equations denotes a group of equations, often known as simultaneous linear equations. In our exploration, we will delve into the techniques for solving pairs of linear equations involving two variables through various methods.

Solving Pairs of Linear Equations in Two Variables

Five strategies are available to address the resolution of pairs of linear equations in two variables, outlined as follows:

1. Graphical Method
2. Substitution Method
3. Cross Multiplication Method
4. Elimination Method
5. Determinant Method

Graphical Method for Solving Linear Equations in Two Variables

Here is a breakdown of the procedural steps for graphically solving linear equations in two variables:

Step 1: To solve a system of two equations involving two variables graphically, create a graph for each equation. You can learn the process here or follow steps 2 and 3 below.

Step 2: For manual graphing of an equation, transform it into the form y = mx + b by solving for y.

Download PDF Linear Equations in two Variables

Step 3: Begin by substituting values of x, such as 0, 1, 2, and so forth, to determine the corresponding y-values, or vice versa.

Step 4: Identify the point at which both lines intersect on the graph.

Step 5: The point of intersection signifies the solution to the provided system of equations.

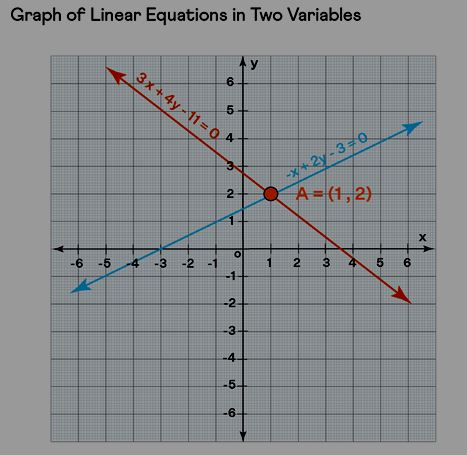
Illustration: Determine the solution of the subsequent system of equations using a graphical approach.

Equations:

-x + 2y - 3 = 0

3x + 4y - 11 = 0

Resolution: By graphing the equations and examining their intersection, we find that both lines converge at the point (1, 2). Consequently, the solution to the provided system of linear equations is x = 1 and y = 2.

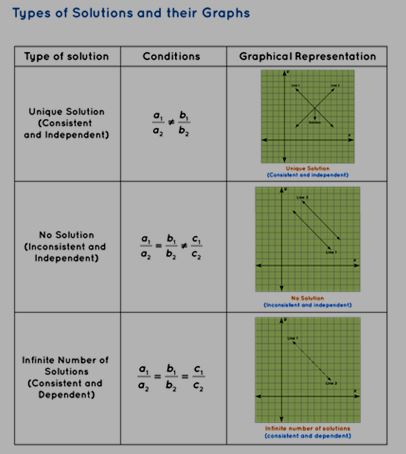
However, it's important to note that intersections don't always occur. Occasionally, the lines might run in parallel, signifying that pairs of linear equations in two variables lack a solution. On the contrary, there are instances where both lines coincide, implying that every point along that line is a solution to the given system. This scenario results in the system possessing an infinite number of solutions.

Consistent and Inconsistent System of Linear Equations:

In cases where a system possesses a solution, it is referred to as a consistent system. Conversely, if no solution exists, the system is termed inconsistent.

Independent and Dependent System of Linear Equations:

When a system possesses a sole and distinct solution, it is categorized as an independent system. Alternatively, if it harbors an infinite array of solutions, it falls under the classification of a dependent system, signifying that one variable hinges upon the other.

Take into account a system of two linear equations: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0. By analyzing these equations, we can ascertain the conditions under which a linear system with two variables is either consistent or inconsistent and whether it is independent or dependent.

Method of Substitution

To effectively solve a system of two linear equations in two variables through the substitution method, adhere to the following sequence of steps:

Step 1: Resolve one of the equations to isolate one of the variables.

Step 2: Substitute the value obtained in Step 1 into the other equation, rendering it an equation with a sole variable.

Step 3: Solve this derived equation for the variable.

Step 4: Subsequently, substitute the value determined in Step 3 into either of the original equations to ascertain the value of the other variable.

Cross Multiplication Method

Let's consider a linear equation system: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.

For solving this system using the cross multiplication method, we begin by arranging the coefficients of x, y, and constants in the given manner:

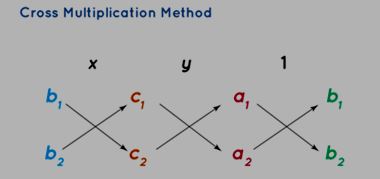
Cross Multiplication Method for Solving Linear Equations in Two Variables

In the above representation, the arrows indicate that these coefficients need to be multiplied. Following this, we establish the subsequent equation by performing cross-multiplication and subtracting the resultant products:

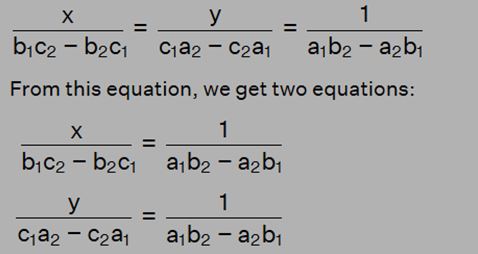
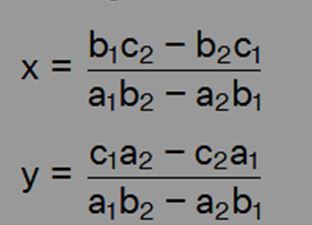
Method of Elimination

To effectively solve a system of linear equations in two variables using the elimination method, follow these stepwise instructions:

Step 1: Arrange the equations in standard form: ax + by + c = 0 or ax + by = c.

Step 2: Determine if the addition or subtraction of the equations would eliminate one of the variables.

Step 3: If not, multiply one or both equations by the coefficient of 'x' or 'y' to enable their addition or subtraction, leading to the elimination of one variable.

Step 4: Solve the resulting single-variable equation.

Step 5: Subsequently, substitute the derived value into either of the initial equations to determine the value of the other variable.

Determinant Method

The determinant of a 2x2 matrix is acquired by cross-multiplying elements, commencing from the upper-left corner, and subsequently subtracting the products.

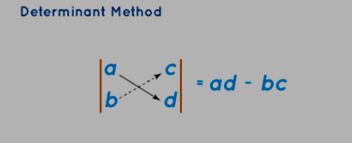
Let's consider a linear equation system in two variables: a1x + b1y = c1 and a2x + b2y = c2. To solve this using the determinant method, often referred to as Cramer's Rule, adhere to the subsequent steps:

Step 1: Start by computing the determinant formed by the coefficients of 'x' and 'y' and label it as Δ.

Step 2: Compute the determinant Δx by substituting the first column of Δ with the constants.

Step 3: Calculate the determinant Δy by substituting the second column of Δ with the constants.

The solution to the given linear equation system is determined using the following formulas:

x = Δx / Δ

y = Δy / Δ

Points to Remember

• A linear equation involving two variables takes the structure ax + by + c = 0, where x and y stand as the variables, while a, b, and c are real numbers.
• A set of linear equations consists of pairs like a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, and its solution corresponds to a pair of values (x, y) that simultaneously fulfill both equations.
• Solving linear equations in two variables necessitates a minimum of two equations.
• A linear equation with two variables yields an unbounded array of solutions.